高中 数学
已知椭圆 的左焦点为
的左焦点为 ,离心率为
,离心率为 , 点
, 点 在椭圆上且位于第一象限,直线
在椭圆上且位于第一象限,直线 被圆
被圆 截得的线段的长为
截得的线段的长为 .(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于
.(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于 ,求直线OP( O 为原点)的斜率的取值范围
,求直线OP( O 为原点)的斜率的取值范围
 的左焦点为
的左焦点为 ,离心率为
,离心率为 , 点
, 点 在椭圆上且位于第一象限,直线
在椭圆上且位于第一象限,直线 被圆
被圆 截得的线段的长为
截得的线段的长为 .(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于
.(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于 ,求直线OP( O 为原点)的斜率的取值范围
,求直线OP( O 为原点)的斜率的取值范围-
(1) 求直线
 的斜率
的斜率
-
(2) 求椭圆的方程
-
(3) 设动点
 在椭圆上,若直线
在椭圆上,若直线 的斜率大于
的斜率大于 , 求直线
, 求直线 (
( 为原点)的斜率的取值范围
为原点)的斜率的取值范围
已知直线  ,
,  互相垂直,则
互相垂直,则  的值是( )
的值是( )
 ,
,  互相垂直,则
互相垂直,则  的值是( )
的值是( )
A . 0
B . 1
C . 0或-1
D . 0或1
在直角坐标系  中,过点
中,过点  的直线
的直线  的倾斜角为
的倾斜角为  ,以坐标原点为极点,
,以坐标原点为极点,  轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线  的极坐标方程为
的极坐标方程为  ,直线
,直线  与曲线
与曲线  的交点为
的交点为  ,
,  .
.
 中,过点
中,过点  的直线
的直线  的倾斜角为
的倾斜角为  ,以坐标原点为极点,
,以坐标原点为极点,  轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线  的极坐标方程为
的极坐标方程为  ,直线
,直线  与曲线
与曲线  的交点为
的交点为  ,
,  .
.
-
(1) 求曲线
 的直角坐标方程;
的直角坐标方程;
-
(2) 求
 及
及  的值.
的值.
已知  中,角
中,角  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  ,且
,且  ,
,  ,
,  成等差数列,
成等差数列,  ,
,  ,则
,则  的面积为( )
的面积为( )
 中,角
中,角  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  ,且
,且  ,
,  ,
,  成等差数列,
成等差数列,  ,
,  ,则
,则  的面积为( )
的面积为( )
A .  B .
B . 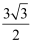 C .
C .  D .
D . 
 B .
B . 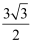 C .
C .  D .
D . 
已知函数 , 设
, 设 ,
,  ,
,  , 则a,b,c的大小关系为( )
, 则a,b,c的大小关系为( )
 , 设
, 设 ,
,  ,
,  , 则a,b,c的大小关系为( )
, 则a,b,c的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
图中阴影部分的面积等于.

如图,△  内接于圆
内接于圆  ,
,  是圆
是圆  的直径,四边形
的直径,四边形  为平行四边形,
为平行四边形,  平面
平面  ,
,  .
.
 内接于圆
内接于圆  ,
,  是圆
是圆  的直径,四边形
的直径,四边形  为平行四边形,
为平行四边形,  平面
平面  ,
,  .
.
-
(1) 求证:
 ⊥平面
⊥平面  ;
;
-
(2) 设
 ,
,  表示三棱锥
表示三棱锥  的体积,求函数
的体积,求函数  的解析式及最大值.
的解析式及最大值.
如图程序输出的结果是( )

A . 3,4
B . 4,4
C . 3,3
D . 4,3
直线y=kx+b与曲线 相切于点(2,3),则b的值为 ( )
相切于点(2,3),则b的值为 ( )
 相切于点(2,3),则b的值为 ( )
相切于点(2,3),则b的值为 ( )
A . -3
B . 9
C . -15
D . -7
证明:
-
(1)
 =cosθ
=cosθ
-
(2) sin4α﹣cos4α=2sin2α﹣1.
已知直线 的方向向量是
的方向向量是 , 平面
, 平面 的法向量是
的法向量是 , 则
, 则 与
与 的位置关系是( )
的位置关系是( )
 的方向向量是
的方向向量是 , 平面
, 平面 的法向量是
的法向量是 , 则
, 则 与
与 的位置关系是( )
的位置关系是( )
A .  B .
B .  C .
C .  与
与 相交但不垂直
D .
相交但不垂直
D .  或
或
 B .
B .  C .
C .  与
与 相交但不垂直
D .
相交但不垂直
D .  或
或
某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是( )
A . 新农村建设后,种植收入减少
B . 新农村建设后,其他收入增加了一倍以上
C . 新农村建设后,养殖收入增加了一倍
D . 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
若  是方程
是方程  的解,
的解,  是方程
是方程  的解,则
的解,则  等于( )
等于( )
 是方程
是方程  的解,
的解,  是方程
是方程  的解,则
的解,则  等于( )
等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
与直线3x﹣2y=0的斜率相等,且过点(﹣4,3)的直线方程为( )
A . y﹣3=﹣ (x+4)
B . y+3=
(x+4)
B . y+3= (x﹣4)
C . y﹣3=
(x﹣4)
C . y﹣3= (x+4)
D . y+3=﹣
(x+4)
D . y+3=﹣ (x﹣4)
(x﹣4)
 (x+4)
B . y+3=
(x+4)
B . y+3= (x﹣4)
C . y﹣3=
(x﹣4)
C . y﹣3= (x+4)
D . y+3=﹣
(x+4)
D . y+3=﹣ (x﹣4)
(x﹣4)
有4名男生、5名女生,全体排成一行,问下列情形各有多少种不同的排法?
(1)甲不在中间也不在两端![]() ;
;
(2)甲、乙两人必![]() 须排在两端;
须排在两端;
(3)男女相间.
由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1 B.2![]() C.
C.![]() D.3
D.3
已知圆上的点![]() 关于直线
关于直线![]() 的对称点仍在此圆上,且该圆截
的对称点仍在此圆上,且该圆截
直线![]() 所得的弦长为
所得的弦长为![]() ,求此圆的方程。
,求此圆的方程。
设直角三角形的两直角边的长分别为![]() ,斜边长为
,斜边长为![]() ,斜边上的高为
,斜边上的高为![]() ,则有
,则有![]() 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论:
①![]() ;②
;②![]() ;③
;③ ![]() ;④
;④![]() .
.
其中正确结论的序号是 ;进一步得到的一般结论是 .
若函数f(x)为定义在R上的奇函数,其导函数为f′(x),对任意实数x满足![]() ,则不等式
,则不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- 下列有关细胞物质组成的叙述,正确的是 A.在人体活细胞中氢原子的数目最多 B.肌肉细胞中含量最多的化合物是
- 2011年,是辛亥革命100周年,全国各地举行了不同形式的纪念活动。在纪念活动讲话中说,辛亥革命后,接受这场革命洗礼的中
- 阅读理解。阅读下列材料,从A、B、C、D四个选项中选出最佳答案。 There are lots ofpopular wr
- Fe3+、SO42﹣、Al3+和X四种离子以物质的量之比2:4:1:1大量共存于同一溶液中,X可能是 A.Br﹣ B.
- 右图漫画《迫降》所蕴含的哲学道理有( ) ①上层建筑对经济基础具有反作用 ②社会存在决定社会意识 ③意识有时也能
- 若为实数,则 “0<ab<1”是“b<”的 A.充分而不必要条件
- 阅读下面的文字,完成1—3题。 警惕“生态癌症”——蓝藻 蓝藻是地球上最早出现的生物之一,亿万年来,蓝藻默默地为地球提供
- In the past ten years, Government has ____ the price of cert
- 有科学家提出回收利用CO2的构想:将工厂排出的气体(含较多CO2)吹入碳酸钾溶液,从溶液中提取出CO2,又在合成塔使之变
- 1790年,有一个法国人写道:“20年前,说法语是荒唐可笑的事。……在今日的城镇,所有市民只说法语。”表明法国
- 如图13-5-8所示,两等量异种电荷在真空中相隔一定距离,OO′表示两点电荷连线的中垂面,在两点电荷所在竖直平面上取图示
- 地震来临时,谭千秋老师张开双臂护住四个学生,学生们得救了,谭老师却牺牲了;同样是地震来临,同样是教师,范美忠却将学生的安
- 我们主要从三个方面讨论一个化学反应的原理,其中不属于这三个方面的是 A、反应进行的方向 B、反应的快慢 C、
- 有一种卫星叫做极地卫星,其轨道平面与地球的赤道平面成900角,它常应用于遥感探测。假设有一个极地卫星绕地球做匀速圆周运动
- 胡适1923年给友人的信中写到:“25年来,只有三个杂志可代表三个时代,可以说创造了三个新时代:一是《时务报》,二是《新
- “神十”飞天标志着我国航天事业的长足发展,那么要使卫星绕地球做匀速圆周运动的最小地面发射速度是( ) A.
- 下列关于糖类、蛋白质、油脂和纤维素的说法中,正确的是 A.它们的组成中都有C、H、O、N等元素 B.在一定条件下,它们都
- 下列各组中的X和Y两种原子,化学性质一定相似的是() A.X原子和Y原子最外层都只有1个电子 B.X原子的核外电子排布式
- My classmate lent me a(an) so that Iwouldn’t get wet in
- 提取下列材料中的要点,整合成一个单句,解释“漫画”。(不超过50个字) ①漫画是绘画的一种。 ②漫画在内容上大多描绘现实




