高中 数学
如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0).且点C与点D在函数 的图像上.若在矩形ABCD内随机取一点,则该点取自阴影部分的概率等于( )
的图像上.若在矩形ABCD内随机取一点,则该点取自阴影部分的概率等于( )

 B .
B .  C .
C . 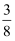 D .
D . 
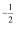 +x
+x 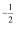 =( )
=( )
 D .
D . 
 x的值域为[﹣1,1],则函数f(x)的定义域是( )
x的值域为[﹣1,1],则函数f(x)的定义域是( )
 ,
,  ]
B . [﹣1,1]
C . [
]
B . [﹣1,1]
C . [  ,2]
D . (﹣∞,
,2]
D . (﹣∞,  ]∪[
]∪[  ,+∞)
,+∞)
 的圆心角为
的圆心角为  ,周长为4.那么当其面积取得最大值时,
,周长为4.那么当其面积取得最大值时,  的值是.
的值是.
(Ⅰ)试求c﹣a的值;
(Ⅱ)若f(x)≤g(x)+a+1恒成立,求实数a的取值范围.
 是定义在
是定义在 上的奇函数,
上的奇函数, 是
是 的导函数,当
的导函数,当 时,
时, , 且
, 且 , 则不等式
, 则不等式 的解集是( )
的解集是( )
 B .
B .  C .
C .  D .
D . 
 成立的x的集合是.
成立的x的集合是.
 ,若
,若  中为整数的解有且仅有一个,则实数
中为整数的解有且仅有一个,则实数  的取值范围是.
的取值范围是.
 是定义在
是定义在  上的奇函数,当
上的奇函数,当  时,
时,  ,则下列说法正确的是( )
,则下列说法正确的是( )
 有2个零点
B . 当
有2个零点
B . 当  时,
时,  C . 不等式
C . 不等式  的解集是
的解集是  D .
D .  ,都有
,都有 
 满足
满足 , 且
, 且 , 则当
, 则当 时,
时, ( )
( )
 B .
B .  C .
C .  D .
D . 
 的解集为( )
的解集为( )
所用的时间(天数) | 10 | 11 | 12 | 13 |
通过公路l的频数 | 20 | 40 | 20 | 20 |
通过公路2的频数 | 10 | 40 | 40 | 10 |
假设汽车A只能在约定日期(某月某日)的前11天出发,汽车B只能在约定日期的前12天出发(将频率视为概率).
(I)为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径;
(Ⅱ)若通过公路l、公路2的“一次性费用”分别为3.2万元、1.6万元(其他费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到;每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,生产商将支付给销售商2万元.如果汽车A,B按(I)中所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.
 ,则方程
,则方程  表示的圆的个数为( )
表示的圆的个数为( )
-
(1) 已知
 , 求
, 求 的最小值;
的最小值;
-
(2) 若
 , 求
, 求 的最大值.
的最大值.
设地球表面某地正午太阳高度角为θ,ξ为此时太阳直射纬度,φ为该地的纬度值,则有θ=90°﹣|φ﹣ξ|.根据地理知识,武汉地区的纬度值约为北纬30°,当太阳直射南回归线(此时的太阳直射纬度为﹣23°26')时物体的影子最长,如果在武汉某高度为h0的楼房北边盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡(如图所示),两楼的距离应至少约为h0的( )倍?(注意tan36°34′=0.75)

A.0.5倍 B.0.8倍 C.1倍 D.1.4倍
如图,在△ABC中,AB=AC=BC=2,则![]()
![]() =( )
=( )


A.1 B.﹣1 C.2 D.﹣2
已知a=log23.4,b=log43.6,c=log30.3,则( )
(A)a>b>c (B)b>a>c
(C)a>c>b (D)c>a>b
A.
C.
- 如图所示,是甲、乙两组拔河比赛的场景,不计绳重,下列说法错误的是………( )A.比赛时,选体重大的运动员,能增大对
- I just wonder____ that makesher so excited. A. why itdoes
- 数列满足表示前n项之积,则的值为( ) A. -3 B.
- With some technical problems to be solved, it may be a while
- 植物体细胞杂交技术的结果是 A.产生杂种植株 B.产生新的细胞壁 C.原生质体融合 D.形
- 已知X、Y、Z为三种原子序数相连的元素,最高价氧化物对应水化物的酸性相对强弱是: HXO4>H2YO4>H3ZO4。则下
- 如图所示,在磁感应强度为B的匀强磁场中有固定的金属框架ABC,已知∠B=θ,导体棒DE在框架上从B点开始在外力作用下,沿
- 补写出下列名篇名句中的空缺部分。(任选1个小题) (1)乃使蒙恬北筑长城而守藩篱,
- I arrived late and missed the flight. I ____ the traffic to
- (2012年3月东北四校一模)如图所示,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之
- 下列实验操作中,正确的是A.熄灭酒精灯B.倾倒液体C.称量固体D.检查气密性
- 将“b”字放在显微镜下观察,视野内看到( ) A.b B.d C.q D.p
- 下图示生物新物种形成的基本环节,对图示分析正确的是A.图中A表示基因突变和基因重组,为进化提供原材料 B.种群基因频率的
- 请写一段话介绍一部文学名著。要求:(1)从《水浒传》、《西游记》和《繁星·春水》中任选一部。(2)这段话中必须选用下列词
- —What did he say just now? —He asked me_________, A. when my
- 1998年初,震惊全国的山西朔州假酒案,数百人中毒,这批假酒中的有毒物质是() A.酒精 B.醋酸 C.甲醇 D.氯化钠
- ______ in the regulations that you shouldnot tell others the
- 一质量为m的带电液滴以竖直向下的初速度V0进入某电场中。由于电场力和重力的作用,液滴沿竖直方向下落一段距离h后,速度变为
- He admits that his political life is. A.at stake B.at danger
- K¯介子方程为K¯→π¯+π0,其中K¯介子和π¯介子带负的基元电荷,π0介子不带电。一个K¯介子沿垂直于磁场的方向射入



