高中 数学
执行如图的程序,若输出的a是4,b是1,则输入的a值x应为

已知命题p:∀x∈(0,+∞),3x>2x , 命题q:∃x∈(﹣∞,0),3x>2x,则下列命题为真命题的是( )
A . p∧q
B . p∧(¬q)
C . (¬p)∧q
D . (¬p)∧(¬q)
渐近线方程为x±y=0的双曲线的离心率是( )
A .  B . 1
C .
B . 1
C .  D . 2
D . 2
 B . 1
C .
B . 1
C .  D . 2
D . 2
已知函数 有两个零点,分别为
有两个零点,分别为 ,
,  , 且
, 且 , 则
, 则 的取值范围是( )
的取值范围是( )
 有两个零点,分别为
有两个零点,分别为 ,
,  , 且
, 且 , 则
, 则 的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数  的图象大致是( )
的图象大致是( )
 的图象大致是( )
的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,则“
,则“  ”是“
”是“  ”( )
”( )
 ,则“
,则“  ”是“
”是“  ”( )
”( )
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
设全集U={﹣1,0,1,2,3},A={﹣1,0,1},B={﹣1,2,3},则∁UA∩B=( )
A . {﹣1}
B . {2,3}
C . {0,1}
D . B
如图是某赛季甲乙两名篮球运动员每场比赛得分的茎叶图,则甲乙两人比赛得分的中位数之和是.

下列四组函数,表示同一函数的是( )
A . f (x)=  ,g(x)=x
B . f (x)=x,g(x)=
,g(x)=x
B . f (x)=x,g(x)=  C . f (x)=
C . f (x)=  ,g(x)=
,g(x)=  D . f (x)=x,g(x)=
D . f (x)=x,g(x)= 
 ,g(x)=x
B . f (x)=x,g(x)=
,g(x)=x
B . f (x)=x,g(x)=  C . f (x)=
C . f (x)=  ,g(x)=
,g(x)=  D . f (x)=x,g(x)=
D . f (x)=x,g(x)= 
已知动点 到定点
到定点 的距离与它到定点
的距离与它到定点 的距离之比为
的距离之比为 .
.
 到定点
到定点 的距离与它到定点
的距离与它到定点 的距离之比为
的距离之比为 .
.
-
(1) 求动点
 的轨迹
的轨迹 的方程;
的方程;
-
(2) 若圆
 与轨迹
与轨迹 相交于
相交于 两点,线段
两点,线段 的长.
的长.
2016年某市政府出台了“2020年创建全国文明城市  简称创文
简称创文  ”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:
”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:  调查对象为本市市民,被调查者各自独立评分;
调查对象为本市市民,被调查者各自独立评分;  采用百分制评分,
采用百分制评分,  内认定为满意,80分及以上认定为非常满意;
内认定为满意,80分及以上认定为非常满意;  市民对公交站点布局的满意率不低于
市民对公交站点布局的满意率不低于  即可进行验收;
即可进行验收;  用样本的频率代替概率.
用样本的频率代替概率.
 简称创文
简称创文  ”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:
”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:  调查对象为本市市民,被调查者各自独立评分;
调查对象为本市市民,被调查者各自独立评分;  采用百分制评分,
采用百分制评分,  内认定为满意,80分及以上认定为非常满意;
内认定为满意,80分及以上认定为非常满意;  市民对公交站点布局的满意率不低于
市民对公交站点布局的满意率不低于  即可进行验收;
即可进行验收; 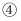 用样本的频率代替概率.
用样本的频率代替概率. 
-
(1) 求被调查者满意或非常满意该项目的频率;
-
(2) 若从该市的全体市民中随机抽取3人,试估计恰有2人非常满意该项目的概率;
-
(3) 已知在评分低于60分的被调查者中,老年人占
 ,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记
,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记  为群众督查员中老年人的人数,求随机变量
为群众督查员中老年人的人数,求随机变量  的分布列及其数学期望
的分布列及其数学期望  .
.
下列四个图形中,是函数图象的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
一组统计数据  与一组统计数据
与一组统计数据  相比较是( )
相比较是( )
 与一组统计数据
与一组统计数据  相比较是( )
相比较是( )
A . 标准差相同
B . 中位数相同
C . 平均数相同
D . 以上都不同
如图,在三棱锥P﹣ABC中,△PAB是正三角形,在△ABC中,AB⊥BC,且D、E分别为AB、AC的中点.

-
(1) 求证:DE∥平面PBC;
-
(2) 求异面直线AB与PE所成角的大小.
若复数 (其中
(其中 为虚数单位)所对应的向量分别为
为虚数单位)所对应的向量分别为 和
和 , 则
, 则 的面积为.
的面积为.
 (其中
(其中 为虚数单位)所对应的向量分别为
为虚数单位)所对应的向量分别为 和
和 , 则
, 则 的面积为.
的面积为.
已知函数![]() .
.
(1)若函数![]() 的最小值是
的最小值是![]() ,且c=1,
,且c=1,
 求F(2)+F(-2)的值;
求F(2)+F(-2)的值;
(2)若![]() ,且
,且![]() 在区间(0,1]上恒成立,试求b的取值范围.
在区间(0,1]上恒成立,试求b的取值范围.
设函数f(x)在点x0附近有定义,且有f(x0+Δx)-f(x0)=aΔx+b(Δx)2(a,b为常数),则( )
A.f′(x)=a B.f′(x)=b
C.f′(x0)=a D.f′(x0)=b
解关于![]() 的不等式
的不等式![]()
A.
已知某地区中小学生人数和近视情况分别如图甲和图乙所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取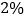 的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
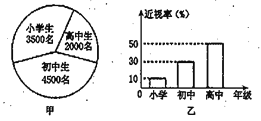
A. 100,10 B. 100,20 C. 200,10 D. 200,20

A. 100,10 B. 100,20 C. 200,10 D. 200,20
最近更新
- “调整优化经济结构,是促进经济发展、提高经济效益和质量的根本性措施之一。”这一论断蕴涵的哲理是 A.构成事物的成分在排列
- 在三棱锥P﹣ABC中,PA,PB,PC两两互相垂直,且AB=4,AC=5,则BC的取值范围是.
- 下列有关家用电器性能及使用的判断,其中正确的是 ( )A.空调机和电风扇都可以降低室内温度 B.微
- 有关四大区域农业发展制约因素的叙述,错误的是 A. 北方地区——热量 B. 南方地区——洪涝 C. 青藏地区—
- 下列有关细胞结构和功能的叙述中,正确的是( ) A.有中心体的细胞一定不会发生质壁分离现象 B.溶酶
- 电量为q的点电荷,在两个固定的等量异种电荷+Q和-Q的连线的垂直平分线上移动,则下列说法中正确的是( )
- 补写下列名篇名句中的空缺部分。(任选3题,多选则按前3题计分) ①______,不能十步;______,功在不舍。(荀子
- .若满足方程组的x、y的值相等,则k=_______.【解析】作y=x的代换,先求出x、y 的值.
- 一个物体放在水平地面上,分别受到外力F的作用时,如图所示,物体对地面的压力大于物体的重力是:
- 计算:
- 将下列集合用区间表示出来.(1){x|x≥1}=__________;(2){x|≥0}=__________;(3){
- 用橡皮筋弹出去的飞机模型仍然继续向前运动,是因为( ) A.飞机受到惯力 B.飞机受到橡皮筋的弹力 C.飞机具有惯性 D
- 17、下列各句中划线成语的使用,全都正确的一项是:( )(3分) ①现在一些大学生制作简历时,多彩色打印,铜
- The problem _______ you argued about yesterday has been solv
- 下列各项中注音有误的一项是( ) A、一幢房屋zhuàng彤云密布tóng 瞳孔tóng B、dì 瓜熟
- 已知a2+b2+4a-2b+5=0,则= .
- 下面词语中有四个错别字,请找出来并改正。(4分)别出新裁 急不遐择 娇柔造作 消声匿迹错别字 改正
- 21.(5分)水是一种重要的物质,在实验室和日常生活中有着十分重要的作用。请根据下列提示简要回答问题: (1)请列举二个
- (2011·潍坊)下列关于细胞的说法,正确的是() A.细胞体积越大,物质运输速率越高 B.有分泌功能的细胞才存在高尔基
- 物体原来静止在光滑的水平面上,现在奇数秒内由于受恒力作用做加速度为2m/s2的匀加速直线运动,偶数秒内做匀速运动,其V-



