高中 数学
(x2﹣  )8的二项展开式中x7项的系数为.
)8的二项展开式中x7项的系数为.
 )8的二项展开式中x7项的系数为.
)8的二项展开式中x7项的系数为.
已知等比数列{an}的公比为2,前4项的和是1,则前8项的和为( )
A . 15
B . 17
C . 19
D . 21
若直线l过点  ,且倾斜角为
,且倾斜角为  ,则l被圆C:
,则l被圆C:  所截得的弦长为.
所截得的弦长为.
 ,且倾斜角为
,且倾斜角为  ,则l被圆C:
,则l被圆C:  所截得的弦长为.
所截得的弦长为.
已知函数  ,且f(x)在区间(0,1]上单调递减,则m的取值范围是( )
,且f(x)在区间(0,1]上单调递减,则m的取值范围是( )
 ,且f(x)在区间(0,1]上单调递减,则m的取值范围是( )
,且f(x)在区间(0,1]上单调递减,则m的取值范围是( )
A . (﹣∞,1)∪(1,3]
B . (﹣∞,0]∪(1,3]
C . (﹣∞,0)∪(1,3)
D . (﹣∞,0)∪(1,3]
已知集合  ,集合
,集合  的所有非空子集依次记为:
的所有非空子集依次记为:  ,设
,设  分别是上述每一个子集内元素的乘积.(如果
分别是上述每一个子集内元素的乘积.(如果  的子集中只有一个元素,规定其积等于该元素本身),那么
的子集中只有一个元素,规定其积等于该元素本身),那么  .
.
 ,集合
,集合  的所有非空子集依次记为:
的所有非空子集依次记为:  ,设
,设  分别是上述每一个子集内元素的乘积.(如果
分别是上述每一个子集内元素的乘积.(如果  的子集中只有一个元素,规定其积等于该元素本身),那么
的子集中只有一个元素,规定其积等于该元素本身),那么  .
.
点M的直角坐标是 , 则点M的极坐标为( )
, 则点M的极坐标为( )
 , 则点M的极坐标为( )
, 则点M的极坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数f(x)在R上是减函数,则有( )
A . f(3)<f(5)
B . f(3)≤f(5)
C . f(3)>f(5)
D . f(3)≥f(5)
新高考改革后,某校2000名学生参加物理学考,该校学生物理成绩的频率分布直方图如图所示,若规定分数达到90分以上为A级,则该校学生物理成绩达到A级的人数是( )

A . 600
B . 300
C . 60
D . 30
函数y=lg(3﹣4x+x2)的定义域为M,当x∈M时,则f(x)=2x+2﹣3×4x的最大值为.
已知向量  ,且
,且  ∥
∥  ,则实数a=( )
,则实数a=( )
 ,且
,且  ∥
∥  ,则实数a=( )
,则实数a=( )
A . 1
B . 6
C . 2或1
D . 2
已知随机变量  ,
, 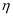 满足
满足  ,若
,若  ,
,  ,则( ).
,则( ).
 ,
, 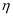 满足
满足  ,若
,若  ,
,  ,则( ).
,则( ).
A .  ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
设 ,
,  ,
,  , 则( )
, 则( )
 ,
,  ,
,  , 则( )
, 则( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知数列  的首项
的首项  的等比数列,其前
的等比数列,其前  项和
项和  中
中  ,
,
 的首项
的首项  的等比数列,其前
的等比数列,其前  项和
项和  中
中  ,
,
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 设
 ,求
,求  .
.
执行如图所示的程序框图,则输出的结果是( ) 

A . 8
B . 13
C . 21
D . 34
设点 是以原点为圆心的单位圆上的一个动点,它从初始位置
是以原点为圆心的单位圆上的一个动点,它从初始位置 出发,沿单位圆顺时针方向旋转角
出发,沿单位圆顺时针方向旋转角 后到达点
后到达点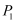 , 然后继续沿单位圆顺时针方向旋转角
, 然后继续沿单位圆顺时针方向旋转角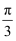 到达点
到达点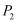 , 若点
, 若点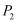 的纵坐标是
的纵坐标是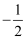 , 则点
, 则点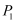 的坐标是.
的坐标是.
 是以原点为圆心的单位圆上的一个动点,它从初始位置
是以原点为圆心的单位圆上的一个动点,它从初始位置 出发,沿单位圆顺时针方向旋转角
出发,沿单位圆顺时针方向旋转角 后到达点
后到达点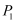 , 然后继续沿单位圆顺时针方向旋转角
, 然后继续沿单位圆顺时针方向旋转角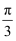 到达点
到达点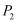 , 若点
, 若点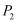 的纵坐标是
的纵坐标是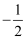 , 则点
, 则点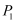 的坐标是.
的坐标是.
对任意实数  ,不等式
,不等式  恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.
 ,不等式
,不等式  恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.
曲线 在
在 处的切线斜率是1,则
处的切线斜率是1,则 .
.
 在
在 处的切线斜率是1,则
处的切线斜率是1,则 .
.

设等差数列{an}满足3a10=5a17,且a1>0,Sn为其前n项和,则数列{Sn}的最大项是( )
A.S24 B.S23 C.S26 D.S27
若关于 的方程
的方程 在区间
在区间 上仅有一个实根,则实数
上仅有一个实根,则实数 的取值范围为( )
的取值范围为( )
A. B.
B.  C.
C.  D.
D. 
A.
最近更新
- 下列物质的贮存方法,正确的是A.硅酸钠溶液和碱性溶液存放在胶塞密封的试剂瓶中B.氢氟酸盛放在棕色试剂瓶中C.液溴盛放在带
- “目贵明,耳贵聪,心贵智,以天下之目视,则无不见也;以天下之耳听,则无不闻也;以天下之心虑,则无不知也。”(春秋《管子•
- “碧玉妆成一树高,万条垂下绿丝绦”,这是大家都熟悉的歌咏春风绿柳的诗句。其实万千枝条及其绿叶,都是由什么直接发育来的(
- 下列实验能观察到明显现象的是A.硝酸银溶液滴入氯化钠溶液中 B.稀盐酸滴入氯化钠溶液中C.氢氧化钠溶
- 已知向量=(4,6),=(3,5),且⊥,∥,则向量=____________.
- 下列物质与其用途相符合的是() ①Cl2—作消毒剂 ②AgBr—制胶卷,感光纸 ③AgI—人工降雨 ④碘—预防甲状腺肿
- 现代家庭部分高清超平彩电采用LED技术,LED是发光二极管简称。在照明应用上,实验室通过实验发现下表中的LED灯和白炽灯
- burn up
- 下列观点符合我国可持续发展的是:( ) A.多子多孙多福气 B.子孙满堂,喜气洋洋 C.有子有女才
- 已知函数. (Ⅰ)关于x的不等式的解集为,且,求a的取值范围; (Ⅱ)是否存在实数,使得当时,成立.若存在给出证明,若不
- 讨论函数在处的连续性与可导性.
- — Why do peoplelike going to Pizza House?— It has themost de
- 本题包括A、B两小题,请自主选做A或B。A、B都选者以A题计分。 A.某同学用光学显微镜观察神经元涂片,图甲和图乙是他看
- 阅读下面的文字,完成各题。 人 物 【罗马尼亚】扬·伯耶舒 有许多好奇的读者曾问我,我作品中的那些人物是怎么挖掘出来的
- 哲学上的物质范畴与自然科学上的物质范畴的关系是( ) A.本质和派生的关系 B.普遍和特殊的关系 C.本质
- 动物运动的意义不包括( ) A.有利于摄取食物 B.有利于逃避敌害
- 信用卡为您带来了多种便利,其功能包括:①购物消费;②存、取款;③转账结算;④理财助手;⑤消费信用。在上述项目中如果按商业
- 军机处的设置,标志着我国君主专制主义中央集权达到顶峰。设立军机处的是()
- 完成句子 1. ——我从来没有去过新图书馆。——我也没有。 —I have to the new library.—
- 下列有关ATP的叙述中正确的是()A. ATP和ADP是同种物质的两种不同的形态 B. 植物细胞中的所有ATP都是由叶绿



