高中 数学
计算: 

已知函数  是定义在
是定义在  上的奇函数,且满足
上的奇函数,且满足  .当
.当  时,
时,  ,则
,则  ,
,  .
.
 是定义在
是定义在  上的奇函数,且满足
上的奇函数,且满足  .当
.当  时,
时,  ,则
,则  ,
,  .
.
若 , 则
, 则 的展开式中常数项为.
的展开式中常数项为.
 , 则
, 则 的展开式中常数项为.
的展开式中常数项为.
已知函数  =
=  曲线
曲线  在点
在点  处的切线方程为
处的切线方程为  .
.
 =
=  曲线
曲线  在点
在点  处的切线方程为
处的切线方程为  .
.
-
(1) 求
 的值;
的值;
-
(2) 求
 的极大值.
的极大值.
已知x是 上的一个随机的实数,则使x满足
上的一个随机的实数,则使x满足 的概率为( )
的概率为( )
 上的一个随机的实数,则使x满足
上的一个随机的实数,则使x满足 的概率为( )
的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
写出具有性质①②③的一个函数 .
.
 .
.
① ;②当
;②当 时,
时, ;③
;③ 是奇函数
是奇函数
正项等比数列  中,存在两项
中,存在两项  使得
使得  ,且
,且  ,则
,则  的最小值是( )
的最小值是( )
 中,存在两项
中,存在两项  使得
使得  ,且
,且  ,则
,则  的最小值是( )
的最小值是( )
A .  B . 2
C .
B . 2
C .  D .
D . 
用数学归纳法证明不等式1+  +
+  +…+
+…+  <2﹣
<2﹣  (n≥2,n∈N+)时,第一步应验证不等式( )
(n≥2,n∈N+)时,第一步应验证不等式( )
 +
+  +…+
+…+  <2﹣
<2﹣  (n≥2,n∈N+)时,第一步应验证不等式( )
(n≥2,n∈N+)时,第一步应验证不等式( )
A . 1+  <2﹣
<2﹣  B . 1+
B . 1+  +
+  <2﹣
<2﹣  C . 1+
C . 1+  <2﹣
<2﹣  D . 1+
D . 1+  +
+  <2﹣
<2﹣ 
 <2﹣
<2﹣  B . 1+
B . 1+  +
+  <2﹣
<2﹣  C . 1+
C . 1+  <2﹣
<2﹣  D . 1+
D . 1+  +
+  <2﹣
<2﹣ 
已知等比数列  中,
中,  ,公比
,公比  ,则
,则  ( )
( )
 中,
中,  ,公比
,公比  ,则
,则  ( )
( )
A . 1
B . -1
C . 3
D . -3
若a2+b2>1,则下列不等式成立的是( )
A . |a|>1且|b|>1
B . |a+b|>1
C . |ab|>1
D . |a|+|b|>1
在△ABC中,E为AC上一点,且 =4
=4 , P为BE上一点,且
, P为BE上一点,且 =m
=m +n
+n (m>0,n>0),则
(m>0,n>0),则 取最小值时,向量
取最小值时,向量 =(m,n)的模为( )
=(m,n)的模为( )
 =4
=4 , P为BE上一点,且
, P为BE上一点,且 =m
=m +n
+n (m>0,n>0),则
(m>0,n>0),则 取最小值时,向量
取最小值时,向量 =(m,n)的模为( )
=(m,n)的模为( )
A .  B .
B .  C .
C .  D . 2
D . 2
 B .
B .  C .
C .  D . 2
D . 2
已知  圆心在直线
圆心在直线  上,且过点
上,且过点 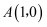 、
、  .
.
 圆心在直线
圆心在直线  上,且过点
上,且过点 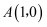 、
、  .
.
-
(1) 求
 的标准方程;
的标准方程;
-
(2) 已知过点
 的直线
的直线  被所截得的弦长为4,求直线
被所截得的弦长为4,求直线  的方程.
的方程.
![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 的面积的最大值是( )
的面积的最大值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
已知x,y满足 ,则
,则![]() 的最大值为__________.
的最大值为__________.
若直线经过![]() 两点,则直线
两点,则直线![]() 的倾斜角是( )
的倾斜角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,
,
则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
△ABC中,![]() ,则△ABC一定是 ( ) A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形
,则△ABC一定是 ( ) A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从贵阳市交通指挥中心随机选取了二环以内50个交通路段,依据交通指数数据绘制的直方图如图所示:
(1)据此直方图估算交通指数T∈[4,8)时的中位数和平均数;
(2)据此直方图求出早高峰二环以内的3个路段至少有两个严重拥堵的概率是多少?
(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严重拥堵为60分钟,求此人所用时间的数学期望.

已知![]() ,其中
,其中![]() , 若
, 若
![]() ,满足
,满足![]() ,且
,且![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
(1)求![]() 的值;
的值;
(2)若对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
已知数列 的前
的前 项和
项和 满足
满足 ,则数列
,则数列 的前10项和等于( )
的前10项和等于( )
A. 380 B. 390 C. 400 D. 410
A. 380 B. 390 C. 400 D. 410
最近更新
- 设集合,,若,则实数的取值范围是 .
- 选出下列各项中字形有误的一项( ) A星罗棋布篷筚生辉 沤心沥血 奴颜卑膝 B兴师动众 兴致勃勃 形同虚设 形形色色C形
- 七边形的外角和为 .
- 全国各地相继开展了与“红段子”内涵类似的“红言颂”、“红色短信”等活动。这些现象成为辐射全国的新红色文化品牌,开创了新时
- 生男还是生女主要取决于母亲,与父亲无关。 ( )
- Idon’t know if she ____ back .If she ____ back, I will let y
- 下图曲线表示农田中,Ⅰ:昼夜温度变化;Ⅱ:光照强度;Ⅲ:植物吸收CO2的变化,请判断下列说法中不正确的是 ()A.从时
- 根据以下要点,写一篇介绍美国残疾女作家海伦·凯勒(Helen Keller)的短文。参考词汇:the deaf-mute
- 20、有关倒平板的操作错误的是( ) A.将灭过菌的培养皿放在火焰旁的桌面上 B.使打开的锥形瓶瓶口迅速通过火焰 C
- 按下图装置进行实验,若x轴表示流入正极的电子 的物质的量,则y
- 关于锂的结构和性质的判断,错误的是(1)与水反应比钠剧烈(2)它的原子半径比钠小(3)它的氧化物暴露于空气易吸收二氧化
- 如图所示,下列器件中属于省力杠杆的是( )
- 在人体内环境中可以发生的生理过程是 A. 神经递质与突触后膜上特异性受体结合 B. 血浆蛋白和血红蛋白的合成 C. 丙
- “m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的() A.充分而不必要条件
- 下列选项中正确反映了1870~1956年中国民族资本主义发展趋势的是
- Never before______ so highly successful in his attempts to f
- 以下每组生物的细胞结构和代谢类型均相同的是 A.硝化细菌和大肠杆菌
- Thereis a boy called Bill in my gym class who has unbearable
- 下列关于文学常识的表述,不正确的一项是( ) A.朱自清是现代文学史上独树一帜的散文家。他的代表作《春》通过
- 下列各组物质,都能与水反应且生成物都能溶于水的是( ) A.NH3、Cl2 B.Na2O2、SO



