高中 数学
不等式  的解集是
的解集是  ,则
,则  的解集是( )
的解集是( )
 的解集是
的解集是  ,则
,则  的解集是( )
的解集是( )
A .  或
或  B .
B .  C .
C .  或
或  }
D .
}
D . 
 或
或  B .
B .  C .
C .  或
或  }
D .
}
D . 
设全集  ,集合
,集合  ,
,  ,则
,则  ( )
( )
 ,集合
,集合  ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,
,  与
与  的夹角为
的夹角为  ,则
,则  ( )
( )
 ,
,  与
与  的夹角为
的夹角为  ,则
,则  ( )
( )
A . 2
B . 3
C . 4
D . 5
地球的北纬45°圈上有A,B两点,它们分别在东经70°和东经160°的经线上,则A,B两点的球面距离与其在此北纬45°圈上劣弧长的比值为
现有一个侧面展开图为半圆形的圆锥,其内部放有一个小球,当小球体积最大时,该圆锥与小球的体积之比是( )
A . 9:4
B . 9:5
C . 3:2
D . 3:1
已知函数f(x)=  +
+  ,则下列命题中正确命题的序号是.
,则下列命题中正确命题的序号是.
 +
+  ,则下列命题中正确命题的序号是.
,则下列命题中正确命题的序号是. ①f(x)是偶函数;
②f(x)的值域是[  ,2];
,2];
③当x∈[0,  ]时,f(x)单调递增;
]时,f(x)单调递增;
④当且仅当x=2kπ±  (k∈Z)时,f(x)=
(k∈Z)时,f(x)=  .
.
如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°

-
(1) 若PA=AB,求PB与平面PDC所成角的正弦值;
-
(2) 当平面PBC与平面PDC垂直时,求PA的长.
四棱锥  与直四棱柱
与直四棱柱  组合而成的几何体中,四边形
组合而成的几何体中,四边形  是菱形,
是菱形,  ,
,  ,
,  ,
,  ,
,  交
交  于
于  ,
,  平面
平面 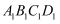 ,
,  为
为  的中点.
的中点.
 与直四棱柱
与直四棱柱  组合而成的几何体中,四边形
组合而成的几何体中,四边形  是菱形,
是菱形,  ,
,  ,
,  ,
,  ,
,  交
交  于
于  ,
,  平面
平面 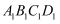 ,
,  为
为  的中点.
的中点. 
-
(1) 证明:
 平面
平面  ;
;
-
(2) 动点
 在线段
在线段  上(包括端点),若二面角
上(包括端点),若二面角  的余弦值为
的余弦值为  ,求
,求  的长度.
的长度.
已知集合  ,集合
,集合  ,集合
,集合  ,命题
,命题  ,命题
,命题  .
.
 ,集合
,集合  ,集合
,集合  ,命题
,命题  ,命题
,命题  .
.
-
(1) 若命题
 为假命题,求实数
为假命题,求实数  的取值范围;
的取值范围;
-
(2) 若命题
 为假命题,求实数
为假命题,求实数  的取值范围.
的取值范围.
已知集合  ,
,  ,则
,则  .
.
 ,
,  ,则
,则  .
.
已知双曲线的标准方程为  ,直线l:y=kx+m(k≠0,m≠0)与双曲线交于不同的两点C、D,若C、D两点在以点A(0,﹣1)为圆心的同一个圆上,则实数m的取值范围是( )
,直线l:y=kx+m(k≠0,m≠0)与双曲线交于不同的两点C、D,若C、D两点在以点A(0,﹣1)为圆心的同一个圆上,则实数m的取值范围是( )
 ,直线l:y=kx+m(k≠0,m≠0)与双曲线交于不同的两点C、D,若C、D两点在以点A(0,﹣1)为圆心的同一个圆上,则实数m的取值范围是( )
,直线l:y=kx+m(k≠0,m≠0)与双曲线交于不同的两点C、D,若C、D两点在以点A(0,﹣1)为圆心的同一个圆上,则实数m的取值范围是( )
A .  B . {m|m>4}
C . {m|0<m<4}
D .
B . {m|m>4}
C . {m|0<m<4}
D . 
 B . {m|m>4}
C . {m|0<m<4}
D .
B . {m|m>4}
C . {m|0<m<4}
D . 
过原点的一条直线与椭圆  交于A,B两点,
交于A,B两点,  为椭圆右焦点,且AB长度等于焦距长,若
为椭圆右焦点,且AB长度等于焦距长,若  ,则该椭圆离心率的取值范围为( )
,则该椭圆离心率的取值范围为( )
 交于A,B两点,
交于A,B两点,  为椭圆右焦点,且AB长度等于焦距长,若
为椭圆右焦点,且AB长度等于焦距长,若  ,则该椭圆离心率的取值范围为( )
,则该椭圆离心率的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M,N分别是AB,PC的中点.

-
(1) 求平面PCD与平面ABCD所成二面角的大小;
-
(2) 求证:MN⊥平面PCD;
-
(3) 当AB的长度变化时,求异面直线PC与AD所成角的可能范围.
已知f(x)的定义域是(0,1),则f[( )x]的定义域为( )
)x]的定义域为( )
 )x]的定义域为( )
)x]的定义域为( )
A . (0,1)
B . ( , 1)
C . (-∞,0)
D . (0,+ ∞)
, 1)
C . (-∞,0)
D . (0,+ ∞)
 , 1)
C . (-∞,0)
D . (0,+ ∞)
, 1)
C . (-∞,0)
D . (0,+ ∞)
在  上定义运算
上定义运算  :
:  .若不等式
.若不等式  对任意实数
对任意实数  成立,则实数
成立,则实数  的取值范围是.
的取值范围是.
 上定义运算
上定义运算  :
:  .若不等式
.若不等式  对任意实数
对任意实数  成立,则实数
成立,则实数  的取值范围是.
的取值范围是.
如图,在四棱锥  中,底面
中,底面  是边长为2的正方形,
是边长为2的正方形,  .
.
 中,底面
中,底面  是边长为2的正方形,
是边长为2的正方形,  .
. 
-
(1) 证明:
 平面
平面  ;
;
-
(2) 若
 ,求二面角
,求二面角  的正弦值.
的正弦值.
在数列{an}中,a1=1,an•an﹣1=an﹣1+(﹣1)n(n≥2,n∈N*),则a3的值是( )
A .  B .
B .  C .
C .  D . 1
D . 1
 B .
B .  C .
C .  D . 1
D . 1
已知函数 是奇函数,且最小正周期为
是奇函数,且最小正周期为 , 则
, 则 (写出符合的一个答案即可).
(写出符合的一个答案即可).
 是奇函数,且最小正周期为
是奇函数,且最小正周期为 , 则
, 则 (写出符合的一个答案即可).
(写出符合的一个答案即可).
按如图所示的流程图运算,若输出k=2,则输入x的取值范围是________.

等差数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,则
,则 ( )
( )
A. 30 B. 35 C. 42 D. 56
A. 30 B. 35 C. 42 D. 56
最近更新
- 下列现象能体现地球公转的是 A.在地球上看太阳升落是“东升西落” B.昼夜交替现象的形成 C.温带地区有明
- 升降机中装一只单摆,当升降机作匀速运动时,单摆的周期为T,现升降机作变速运动,设加速度的绝对值小于g,则下列说法正确的是
- 人类活动对演替的影响是() A. 人类活动加快演替的速度 B. 人类活动减缓演替的进行
- (2011年山东泰安,1题)“2H”表示的意义是A、2个氢元素 B、2个氢原子
- 下列物质中常用于保护食物,以免被微生物侵蚀的是( ) A.酒精 B.食盐
- Kids will often ignore your requests for them to shut of
- 读下图,完成8~9题。8.目前我国所处的区域发展阶段是() A.以传统农业为主体的发展阶段 B.工业化阶段 C.高效益的
- 若某星球的质量和半径均为地球的一半,那么质量为50kg的宇航员在该星球上的重力大约是地球上重力的 A.1/4
- 已知25℃、101kPa下,石墨、金刚石燃烧的热化学方程式分别为 ( ) C(石墨) + O2(g)
- 小强和几位同学在实验室用下列几种装置制取几种气体 (1)写出图中有标号a、b的仪器的名称:① ② (2)
- People use their mouths for many things. They eat, talk, sho
- 以下四种微生物都参与豆腐的发酵,从代谢类型上考虑哪一项与其他三项有明显区别() A.青霉
- (12分)已知反应: (R、R’可表示烃基或官能团)A可进行如下反应(方框内物质均为有机物,部分无机产物已略去)。(
- 一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长
- 下列国家,其煤、铁、石油储量都很丰富的是 A.美国、俄罗斯 B.英国、
- — What question did the teacher ask just now? — She asked ho
- 下列各句中,没有语病的一句是( ) A.当前股民应该果断回避股价被大幅炒高的“题材股”,而且要尽量回避受加息影响比较大
- 下列词语中加点的字的读音完全相同的一组是( ) A.奇数 通缉 放荡不羁 掎角之势 B.按捺纳税刚毅
- 如图,某电场的一条电场线与Ox轴重合,取O点电势为零,Ox方向上各点电势φ随x变化的规律如图所示.若在O点由静止释放一电
- 原子序数为83的元素位于:①第5周期;②第6周期;③ⅣA族;④ⅤA族;⑤ⅡB族.其中正确的组合是() A. ①④



