高中 数学
在直角坐标系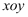 中,抛物线
中,抛物线 与直线
与直线 交于P,Q两点,且
交于P,Q两点,且 .抛物线C的准线与x轴点交于点M,G是以M为圆心,
.抛物线C的准线与x轴点交于点M,G是以M为圆心, 为半径的圆上的一点(非原点),过点G作抛物线C的两条切线,切点分别为A,B.
为半径的圆上的一点(非原点),过点G作抛物线C的两条切线,切点分别为A,B.
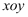 中,抛物线
中,抛物线 与直线
与直线 交于P,Q两点,且
交于P,Q两点,且 .抛物线C的准线与x轴点交于点M,G是以M为圆心,
.抛物线C的准线与x轴点交于点M,G是以M为圆心, 为半径的圆上的一点(非原点),过点G作抛物线C的两条切线,切点分别为A,B.
为半径的圆上的一点(非原点),过点G作抛物线C的两条切线,切点分别为A,B.
-
(1) 求抛物线C的方程;
-
(2) 求
 面积的取值范围.
面积的取值范围.
若 是定义在
是定义在 上的奇函数,且在
上的奇函数,且在 上是增函数,
上是增函数, , 则
, 则 解集是( )
解集是( )
 是定义在
是定义在 上的奇函数,且在
上的奇函数,且在 上是增函数,
上是增函数, , 则
, 则 解集是( )
解集是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知 , 则
, 则 =( )
=( )
 , 则
, 则 =( )
=( )
A . 1
B . 2
C . 3
D . 4
已知函数  ,
,  ,其中e为自然对数的底数.
,其中e为自然对数的底数.
 ,
,  ,其中e为自然对数的底数.
,其中e为自然对数的底数.
-
(1) 求函数
 在x
在x  1处的切线方程;
1处的切线方程;
-
(2) 若存在

 ,使得
,使得  成立,其中
成立,其中  为常数,
为常数,求证:
 ;
; -
(3) 若对任意的
 ,不等式
,不等式  恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
为了得到函数  的图象,只需把函数
的图象,只需把函数  的图象( )
的图象( )
 的图象,只需把函数
的图象,只需把函数  的图象( )
的图象( )
A . 向左平移  个单位长度
B . 向左平移
个单位长度
B . 向左平移  个单位长度
C . 向右平移
个单位长度
C . 向右平移  个单位长度
D . 向右平移
个单位长度
D . 向右平移  个单位长度
个单位长度
 个单位长度
B . 向左平移
个单位长度
B . 向左平移  个单位长度
C . 向右平移
个单位长度
C . 向右平移  个单位长度
D . 向右平移
个单位长度
D . 向右平移  个单位长度
个单位长度
安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A . 12种
B . 18种
C . 24种
D . 36种
已知  ,点
,点  在直线
在直线  上,则当
上,则当  ,
,  的最小值为
的最小值为
 ,点
,点  在直线
在直线  上,则当
上,则当  ,
,  的最小值为
的最小值为
函数f(x)=x3+lnx﹣2零点所在的大致区间是( )
A . (0,1)
B . (1,2)
C . (2,3)
D . (3,4)
已知集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知△ABC,AB=AC=4,BC=2,点D为AB延长线上一点,BD=2,连结CD,则△BDC的面积是,cos∠BDC=.
已知函数f(x)=  ,则f(log23)=.
,则f(log23)=.
 ,则f(log23)=.
,则f(log23)=.
已知  ,
,  ,
,  ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )
 ,
,  ,
,  ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
现代集合论的创始人是( )
A . 高斯
B . 戴德金
C . 维尔斯特拉斯
D . 康托尔
函数 在区间
在区间 的图象大致为( )
的图象大致为( )
 在区间
在区间 的图象大致为( )
的图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  ,若函数
,若函数  无零点,则实数
无零点,则实数  的取值范围为( )
的取值范围为( )
 ,若函数
,若函数  无零点,则实数
无零点,则实数  的取值范围为( )
的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知复数Z满足|Z|=  ,Z2的虚部是2.设Z,Z2 , Z﹣Z2在复平面上的对应点分别为A,B,C,则△ABC的面积为.
,Z2的虚部是2.设Z,Z2 , Z﹣Z2在复平面上的对应点分别为A,B,C,则△ABC的面积为.
 ,Z2的虚部是2.设Z,Z2 , Z﹣Z2在复平面上的对应点分别为A,B,C,则△ABC的面积为.
,Z2的虚部是2.设Z,Z2 , Z﹣Z2在复平面上的对应点分别为A,B,C,则△ABC的面积为.
设复数![]() ,
,![]() 满足
满足![]() ,
,![]() ,则
,则![]() =__________.
=__________.
方程![]() 表示的曲线是( )
表示的曲线是( )
A. 一个圆和一条直线 B. 一个圆和一条射线
C. 一条直线 D. 一个圆
在等差数列![]() 中,
中,![]() 为其前
为其前![]() 项和,若
项和,若![]() ,则
,则![]() ( )
( )
A.60 B.75 C.90 D.105
设命题![]() :方程
:方程![]() 的两根符号不同;命题
的两根符号不同;命题![]() :方程
:方程![]() 的两根之和为3,判断命题“
的两根之和为3,判断命题“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”为假命题的个数为 ( )
”为假命题的个数为 ( )
A.0 B.1 C.2 D.3
最近更新
- 对绿色植物光合作用最有效的一组光是 …() A.红光和黄绿光 B.黄光和蓝紫光 C.红光和橙光 D.红橙光和蓝
- 下图A、B、C及对应面积代表某草原生态系统中的三种生物成分及其在某一年同化的能量。请回答以下问题:(1)三者之间不能建立
- 下列各种现象中,主要由内力作用形成的是() A.北美五大湖 B.长江三角洲 C.云南路南石林 D.夏威夷群岛
- 如图4-5-4所示,长木板平放在地面上,用F=10 N的力拉动木板上的小木块使其匀速前进,但木板静止,则木板的受力个数为
- 人口自然增长率的大小取决于( ) A.经济发达程度 B.
- 把Ba(OH)2溶液滴入到明矾溶液中,使SO42-全部转化成BaSO4沉淀,此时铝元素主要存在形式是( ) A.A l
- 读图,完成1~2题。该图的比例尺大约为 ( ) A.图中 1厘米代表实地距离22 200 000千米
- 在位于坐标原点的波源 S产生一列沿x轴正方向传播的简谐横波,波速 v=300m/s,已知 t=0时,波刚好传播到 x=3
- 我国饮用矿泉水的基本类别是碳酸水、硅酸水和锶水。此外还有锌、锂、溴、碘及硒矿泉水等,这里的锌、锂、溴、碘、硒是指 A
- “水的煮沸”和“水的分解”有什么本质区别?( ) A.前者发生化学变化,后者发生物理变化 B.前者得到纯净物,后
- 在探究串联电路中电压规律的实验中,小红同学将电阻R1、R2串联后接到电源上,如图(a)所示 ① 小红依照图
- 甲、乙两车从同一地点同向行驶,但是甲车做匀速直线运动,其速度为=20米/秒,乙车在甲车行驶至距离出发地125米处时开始以
- 下列大肠杆菌某基因的碱基序列的变化,对其所控制合成的多肽的氨基酸序列影响最大的是(不考虑终止密码子)A.第6位的C被替换
- 读“我国部分省区某年人口出生率、人口自然增长率和人口总数的统计图”,回答1~2题。 1.下列判断正确的是( ) A、
- 中国外汇交易中心公布,2013年1月31日,银行间外汇市场人民币汇率中间价为1美元对人民币6.2795元;2013年9月
- 下列图形中,既是轴对称图形又是中心对称图形的是A B C D
- 近亲结婚会增加后代遗传病的发病率,主要原因在于( ) A.近亲结婚容易使后代产生新的致病基因 B.近亲结婚的双方携带
- 用容量瓶配制一定物质的量浓度的溶液,该容量瓶必须是( ) A.干燥的 B.瓶塞不漏水的 C.用欲配制的溶
- 一质量为m的质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的。今把质点从O点
- 2015年5月,浙江网商银行获批开业,至此首批5家试点民营银行已全部获批开业。民营银行属于私营经济。下列对于私营经济认识



