高中 数学
 中,内角A,B,C的对边分别是a,b,c,且
中,内角A,B,C的对边分别是a,b,c,且  .
.
-
(1) 求
 的值;
的值;
-
(2) 若
 ,求
,求  的面积.
的面积.
附表:
P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
则作出“这种血清能起到预防感冒的作用”出错的可能性不超过( )
 .
.
 (
(  为虚数单位),则复数
为虚数单位),则复数  在复平面上对应的点位于( )
在复平面上对应的点位于( )
 B . y=log2|x|
C . y=1﹣x2
D . y=x3﹣1
B . y=log2|x|
C . y=1﹣x2
D . y=x3﹣1
 、
、  和向量
和向量  、
、  ,下列结论中正确的是( )
,下列结论中正确的是( )
 B .
B .  C . 若
C . 若  ,则
,则  D . 若
D . 若  ,则
,则 
 的焦点为F , 过点F的直线交C于A , B两点,以AB为直径的圆交x轴于M , N , 且当
的焦点为F , 过点F的直线交C于A , B两点,以AB为直径的圆交x轴于M , N , 且当  轴时,
轴时,  .
. 
-
(1) 求抛物线C的方程;
-
(2) 若直线AN , AM分别交抛物线C于G , H(不同于A),直线AB交GH于点P , 且直线AB的斜率大于0,证明:存在唯一这样的直线AB使得B , H , P , M四点共圆.
 中,
中,  ,
,  ,则该椭圆标准方程为
,则该椭圆标准方程为 

 B .
B .  C .
C .  D .
D . 
 (其中
(其中  的值为( )
的值为( )
 B .
B .  C .
C .  D .
D . 如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0 , y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1 , l2 , l1与l2相交于点M.
(Ⅰ)求p的值;
(Ⅱ)求动点M的轨迹方程.

 ,
,  . 若实数a,b(a,b均大于1)满足
. 若实数a,b(a,b均大于1)满足
 , 则下列说法正确的是( )
, 则下列说法正确的是( )
 在
在 上单调递减
B . 函数
上单调递减
B . 函数 的图像关于
的图像关于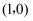 中心对称
C .
中心对称
C .  D .
D . 
 B .
B .  C .
C .  或-1
D .
或-1
D .  或
或
 的前
的前  项和为
项和为  ,若已知
,若已知  ,则( )
,则( )
 B .
B .  C .
C .  D .
D . 
 .则
.则  的最大值为.
的最大值为.
 , 集合
, 集合 , 则
, 则 ( )
( )
 B .
B .  C .
C .  D .
D . 
若平面![]() 和直线
和直线![]() ,
,![]() 满足
满足![]() ,
,![]() ,则
,则![]() 与
与![]() 的位置关系一定是( )
的位置关系一定是( )
A.相交 B.平行 C.异面 D.相交或异面
如图,设椭圆![]() 长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是
长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是![]() .
.

(1)求椭圆C1的标准方程;
(2)过F作直线l交抛物线C2于A,B两点,过F且与直线l垂直的直线交椭圆C1于另一点C,求△ABC面积的最小值,以及取到最小值时直线l的方程.
学校将甲、乙、丙、丁4名教师分配到A、B、C、D四个课外活动小组开展活动,每个小组安排1人,由于工作需要,教师甲不能到A组,教师乙不能到B组,那么不同的分配方案共有
A.20种 B.18种 C.14种 D.12种
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶的图表示,则甲、乙两名运动员得分的中位数分别

A.19、13 B.13、19 C.20、18 D.18、20
- 对李贽主张的评述,正确的是 A.认为君主专制是“天下之大害” B.否定孔子是“天生圣人” C.反对以孔子的“是非”为是非
- 下面句子中对“厥”解释错误的一项是( ) ①思厥先祖父。/厥父母勤劳稼穑 (代词 他的、他
- 研究发现,冬小麦在秋冬受低温袭击时,呼吸速率先升高后减低;持续的冷害使根生长迟缓,吸收能力下降,但细胞内可溶性糖的含量有
- 下列实验过程中,始终无明显现象的是() A.CO2通入饱和Na2CO3溶液中 B.SO2通入CaCl2溶液中 C.NH3
- 写作: 呵护孩子,让孩子健康成长,是父母的责任;孝敬父母,让父母安享天伦之乐,是儿女的责任;因材施教,教书育人,是教师的
- 木炭还原氧化铜和一氧化碳还原氧化铜的实验装置如图K6-11所示。下列说法正确的是()图K6-11 A.木炭、一氧化碳与氧
- 17-18世纪,英美法资产阶级革命爆发的相同原因是( ) A.殖民统治激起了人民的反抗
- 在2A+B==3C+4D反应中,表示该反应速率最快的是 ( ) A.v(A)=0.5mol·L-1·s-1 B.v
- 红、黄、蓝三束单色光,在某介质内以相同的入射角射入真空中,下列说法中正确的是A在该介质中传播时蓝光速度最大 B光从该介质
- “夫天生一人,自有一人之用,不待取给孔子而后足也。若必待取足于孔子,则千古以前无孔子,终不得为人乎?”其核心思想是(
- —Listen! Somebody is coming. —No, _____ is coming. I can’t
- 下列关于科学家及相关事实错误的是 A
- 如图所示,倾角θ=37°的斜面底端B平滑连接着半径r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块,从距地面
- 26.以下关于T细胞作用的叙述最完整的一组是 ①处理抗原②传递抗原③识别抗原 ④分化成记忆细胞⑤分化成效应T细胞 A.①
- In front of our house ______ we used to swim. A. a river
- 在“测定金属丝的电阻率”的实验中,某同学进行了如下测量: (1)用毫米刻度尺测量接入电路中的被测金属丝的有效长度.测量
- (1)如图,画出磁极间磁感线方向。 (2)如图,小明沿水平方向用200N的力推一辆车匀速向左运动。用力的示意图表示车
- 在一个标准大气压下冰水混合物的温度是 0C,沸水的温度是 0C.
- 抓住历史事件相关联的因素,有助于梳理知识,加深理解。以下关联不正确的是 A.明治维新——《大日本帝国宪法》——日本走上发
- More people all over the world get to know Shanghai after t



