高中 数学
 .
.
-
(1) 直接写出此函数的定义域与值域(用区间表示);
-
(2) 证明:对于任意的
 ,都有
,都有  ;
;
-
(3) 用单调性定义证明
 在
在  上是减函数.
上是减函数.
 ,则
,则  .
.
 , 则与
, 则与 垂直的单位向量的坐标是( )
垂直的单位向量的坐标是( )
 或
或 C . (-1,1)
D .
C . (-1,1)
D . 
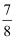 B .
B .  C .
C .  D .
D . 
 的左、右焦点分别为
的左、右焦点分别为  ,
,  ,则能使双曲线C的方程为
,则能使双曲线C的方程为  的是( )
的是( )
 B . 双曲线过点
B . 双曲线过点  C . 渐近线方程为
C . 渐近线方程为  D . 实轴长为4
D . 实轴长为4
 为圆周率,
为圆周率, 为自然对数的底数,则( )
为自然对数的底数,则( )
 B .
B .  C .
C .  D .
D . 
 sin θ(
sin θ(  ∈R),z1=z2 , 则θ等于( )
∈R),z1=z2 , 则θ等于( )
 (k∈Z)
C . 2kπ±
(k∈Z)
C . 2kπ±  (k∈Z)
D . 2kπ+
(k∈Z)
D . 2kπ+  (k∈Z)
(k∈Z)
-
(1) 若{an}是等比数列,S3=35,求{an}的通项公式;
-
(2) 若{an}是等差数列,S5=S6 , 求Sn的最大值.
 满足
满足  ,设
,设  ,且
,且  ,则数列
,则数列  的首项
的首项  的值为( )
的值为( )
 B . 1
C .
B . 1
C .  D . 2
D . 2
 ,则甲队以四比一战胜乙队的概率为( )
,则甲队以四比一战胜乙队的概率为( )
 B .
B . 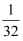 C .
C . 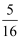 D .
D . 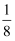
 的前
的前  项和
项和  ,则
,则  ,
,  的最大值为.
的最大值为.
如图,空间四边形 中,
中, ,
,  ,
,  , 点M在线段OA上,且OM=2MA,点N为BC的中点,则
, 点M在线段OA上,且OM=2MA,点N为BC的中点,则 ( )
( )
 B .
B .  C .
C .  D .
D . 
 的长度为
的长度为 , 则该勒洛三角形的面积为.
, 则该勒洛三角形的面积为.
.在平面直角坐标系xOy中,已知曲线C1:![]() (t为参数),C2:
(t为参数),C2: (m为参数).
(m为参数).
(1)将C1,C2的方程化为普通方程,并说明它们分别表示什么曲线;
(2)设曲线C1与C2的交点分别为A,B,O为坐标原点,求△OAB的面积的最小值.
设α,β为两个平面,则α∥β的充要条件是
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
设函数![]() ,对任意实数t都有
,对任意实数t都有![]() 成立,则函数值
成立,则函数值![]() 中,最小的一个不可能是
中,最小的一个不可能是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知奇函数![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
“![]() ”是“
”是“![]() ”的( )条件
”的( )条件
A.充分不必要 B.充要 C. 必要不充分 D.既不充分也不必要
已知 F 1 ,F 2 是椭圆 C: ![]() 的两个焦点,点 M在C 上,则|MF 1 |·|MF 2 |的最大值为
的两个焦点,点 M在C 上,则|MF 1 |·|MF 2 |的最大值为
A.13 B.12 C.9 D.6
- 如图2,直线=+2与双曲线=在第二象限有两个交点,那么m的取值范围在数轴上表示为
- 化学就在我们身边,它与我们的生产、生活息息相关. (1)现有以下几种常见的物质:a.CO2b.小苏打(NaHCO3)c.
- 用如图所示的实验装置测动滑轮的机械效率。滑轮下面挂着的钩码所受重力是1N,向上拉弹簧测力计,使钩码从甲图中的A位置匀速上
- 下列实验操作图示正确的是 A.向酒精灯内填加酒精 B.熄灭酒精灯 C.倾倒液体
- 19世纪中期爆发的具有影响的局部性国际战争是 A.三次英荷战争 B.克里米亚战争 C.英法七年战争
- 做下列实验时,应将温度计水银球插入反应混合液中的是( )A.制蒸馏水 B.制乙烯
- 商品的价值量只能由________决定() A.使用价值
- (10分)用图示装置制取少量乙酸乙酯(酒精灯、铁架台等在图中均已略去),请填空:(1)写出试管a中发生反应的化学方程式
- 面对金融危机的冲击,我国财政部、国家税务总局提高了劳动密集型产品出口退税率。这样做( ) A.有利于增加我国的财政收
- 下列各句中不含通假字的一项是 A.独窦婴争之,由此与错有卻。 B.居无何,而朔妇免身,生男。 C.公子与侯生决,至军,侯
- ________ twice, the postman refused to deliver our letters u
- (一)文言文阅读(19分) 阅读下面的文字,完成10-13题。 祭肜①字次孙,早孤,以至孝见称。
- 下列关于细胞免疫的叙述错误的是( )A.它与体液免疫各自有其独特的作用,又可以相互配合,缺一不可B.效应T细胞产生
- 从石墨中分离出来的石墨烯是最薄、最坚硬、几乎透明的物质,可制成电阻率最小的纳米材料,其结构如图所示。下列关于石墨烯的说法
- 在水平地面上,用20N的水平拉力拉重为50N的小车,使小车沿水平方向前进了10m,此过程中拉力所做的功是() A.200
- 下列属于商品的是 ( )①自产自销的粮食产品 ②赠送同学的礼物 ③向地震灾区空投的援
- 中国近代史上第一个不平等条约是( ) A、《南京条约》 B、《北京条约》 C、《马关条约
- 如图,已知双曲线与直线相交于,两点,过点作轴的垂线 与过点作轴的垂线相交于点,若△的面积为8,则的值为 .
- 阅读下面的文字,回答12――14题。(共15分)诗文中的清明节张巨龄清明,是中华民族的传统节日之一。相传其俗起于西周时期
- 古诗文默写。(8分) ________________,以观沧海。水何澹澹,__________________。《观沧



