高中 数学
已知两条直线l1:x+3y﹣12=0,l2:3tx﹣2y﹣2=0与两坐标轴围成的四边形有外接圆,则此外接圆的方程是
下列关于命题的说法正确的是( )
A . 命题“若 , 则
, 则 ”的逆否命题为真命题
B . “
”的逆否命题为真命题
B . “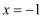 ”是“
”是“ ”的必要不充分条件
C . 命题“
”的必要不充分条件
C . 命题“ ,
,  都是有理数”的否定是“
都是有理数”的否定是“ ,
,  都不是有理数”
D . 命题“若
都不是有理数”
D . 命题“若 , 则
, 则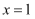 ”的否命题为:“若
”的否命题为:“若 , 则
, 则 ”
”
 , 则
, 则 ”的逆否命题为真命题
B . “
”的逆否命题为真命题
B . “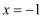 ”是“
”是“ ”的必要不充分条件
C . 命题“
”的必要不充分条件
C . 命题“ ,
,  都是有理数”的否定是“
都是有理数”的否定是“ ,
,  都不是有理数”
D . 命题“若
都不是有理数”
D . 命题“若 , 则
, 则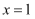 ”的否命题为:“若
”的否命题为:“若 , 则
, 则 ”
”
阅读右边的程序框图,运行相应的程序,当输入的值为10时,输出S的值为( )

A . 45
B . 49
C . 52
D . 54
已知函数 , 若
, 若 , 且
, 且 , 则
, 则 的取值范围是.
的取值范围是.
 , 若
, 若 , 且
, 且 , 则
, 则 的取值范围是.
的取值范围是.
若双曲线C:  的一条渐近线被圆
的一条渐近线被圆  所截得的弦长为2,则C的离心率为( )
所截得的弦长为2,则C的离心率为( )
 的一条渐近线被圆
的一条渐近线被圆  所截得的弦长为2,则C的离心率为( )
所截得的弦长为2,则C的离心率为( )
A . 2
B . 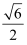 C .
C .  D .
D . 
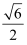 C .
C .  D .
D . 
如图,在平面四边形 中,
中, ,
,  ,
,  .
.
 中,
中, ,
,  ,
,  .
.
-
(1) 当
 ,
,  时,求
时,求 的面积;
的面积;
-
(2) 当
 ,
,  时,求
时,求 .
.
已知M(4,3,-1),记M到x轴的距离为a , M到y轴的距离为b , M到z轴的距离为c , 则( )
A . a>b>c
B . c>b>a
C . c>a>b
D . b>c>a
若  ,
,  ,
,  ,则a,b,c大小关系为( )
,则a,b,c大小关系为( )
 ,
,  ,
,  ,则a,b,c大小关系为( )
,则a,b,c大小关系为( )
A . a>b>c
B . a>c>b
C . c>b>a
D . b>a>c
设随机变量X等可能取值1,2,3,…,n,如果P(X<4)=0.3,那么( )
A . n=3
B . n=4
C . n=10
D . n=9
下列四个命题中的真命题是
A . 经过定点  的直线都可以用方程
的直线都可以用方程  表示;
B . 经过任意两不同点
表示;
B . 经过任意两不同点  、
、  的直线都可以用方程
的直线都可以用方程  表示;
C . 不经过原点的直线都可以用方程
表示;
C . 不经过原点的直线都可以用方程  表示;
D . 斜率存在且不为0,过点
表示;
D . 斜率存在且不为0,过点  的直线都可以用方程
的直线都可以用方程  表示
表示
 的直线都可以用方程
的直线都可以用方程  表示;
B . 经过任意两不同点
表示;
B . 经过任意两不同点  、
、  的直线都可以用方程
的直线都可以用方程  表示;
C . 不经过原点的直线都可以用方程
表示;
C . 不经过原点的直线都可以用方程  表示;
D . 斜率存在且不为0,过点
表示;
D . 斜率存在且不为0,过点  的直线都可以用方程
的直线都可以用方程  表示
表示
已知空间四边形  中,
中,  分别是
分别是  的中点,则下列判断正确的是( )
的中点,则下列判断正确的是( )
 中,
中,  分别是
分别是  的中点,则下列判断正确的是( )
的中点,则下列判断正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知i为虚数单位,复数z=(2﹣i)的模|z|=( )
A . 1
B .  C .
C . 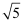 D . 3
D . 3
 C .
C . 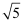 D . 3
D . 3
如果点P在平面区域  上,点Q在曲线x2+(y+2)2=1上,那么|PQ|的最小值为( )
上,点Q在曲线x2+(y+2)2=1上,那么|PQ|的最小值为( )
 上,点Q在曲线x2+(y+2)2=1上,那么|PQ|的最小值为( )
上,点Q在曲线x2+(y+2)2=1上,那么|PQ|的最小值为( )
A .  B .
B .  C .
C .  D .
D . 
已知数列  的前
的前  项和为
项和为  ,
,  ,若存在两项
,若存在两项  ,
,  ,使得
,使得  ,则
,则  的最小值为( )
的最小值为( )
 的前
的前  项和为
项和为  ,
,  ,若存在两项
,若存在两项  ,
,  ,使得
,使得  ,则
,则  的最小值为( )
的最小值为( )
A . 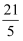 B .
B .  C .
C . 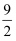 D .
D . 
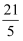 B .
B .  C .
C . 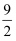 D .
D . 
光线从点A(﹣2, )射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2
)射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2 ),则光线BC所在直线的倾斜角为( )
),则光线BC所在直线的倾斜角为( )
 )射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2
)射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2 ),则光线BC所在直线的倾斜角为( )
),则光线BC所在直线的倾斜角为( )
A .  B .
B . 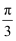 C .
C .  D .
D . 
 B .
B . 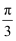 C .
C .  D .
D . 
关于x,y的不等式组  ,表示的区域为D,若区域D内存在满足t≤3x﹣y的点,则实数t的取值范围为( )
,表示的区域为D,若区域D内存在满足t≤3x﹣y的点,则实数t的取值范围为( )
 ,表示的区域为D,若区域D内存在满足t≤3x﹣y的点,则实数t的取值范围为( )
,表示的区域为D,若区域D内存在满足t≤3x﹣y的点,则实数t的取值范围为( )
A . (﹣∞,1]
B . [1,+∞)
C . (﹣∞,5]
D . [5,+∞)
已知函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,则
,则![]() 的取值范围是_____;若不等式
的取值范围是_____;若不等式![]() 有解,则
有解,则![]() 的取值范围是______.
的取值范围是______.
已知点![]() 、
、![]() 是椭圆
是椭圆![]() 的焦点,若点P是椭圆上的一个动点,则
的焦点,若点P是椭圆上的一个动点,则![]() 的最小值是( )
的最小值是( )
A 0 B 1 C 2 D ![]()
如图,正方形![]() 与直角梯形
与直角梯形![]() 所
所
在平面互相垂直,![]() ,
,![]() ,
,![]() .
.
(Ⅰ) 求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求平面![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.

最近更新
- ......
- 下列说法正确的是 A.CH3COOH与NaOH在相同条件下电离程度相等 B.NaCl溶液能导电是因为溶液中有Na+和Cl
- 读“我国某地等压线和河流分布示意图”,回答下列各题。 图中最大的山脉走向大致为 A.东北一西南走向 B.西北一东南走
- 在人类历史发展过程中,每个民族都面临着自身传统文化与外来文化的碰撞。阅读下列材料: 材料一:汉唐虽然也有边患,但魄力究竟
- 下图中“”表示碳原子,“”表示氧原子。 A B C D 其中表示混合物的是________(填图的编
- 在国际单位制中,力学的基本单位是:( ) A.N、m、s B.kg、m、s C.N、kg、
- (2016·深圳第一次调研)(6分)把两根轻质弹簧串联起来测量它们各自的劲度系数,如图甲所示。(1)未挂钩码之前,指针B
- 北宋时对词的发展有突出贡献的词人是( ) A.苏轼 B.辛弃疾 C.李清照
- 函数的最小正周期是 ( ) A.
- 蝴蝶的发育属于完全变态,该过程是( ) A.卵→若虫→成虫 B.卵→蛹→成虫 C.卵→
- 我国青藏地区的居民“身穿绵羊皮缝制的藏袍,白天束带为衣,夜间解带当被”所反映出的自然环境特征是() ①气候寒冷,昼夜温差
- 一定温度下的难溶电解质AmBn在水溶液中达到沉淀溶解平衡时,其Ksp=cm(An+)×cn(Bm-),称为难溶电解质的溶
- 右图中阴影为某农作物分布区,黑粗实线为较大范围的大陆轮廓,下列有关该种植业特点的叙述,错误的是A.科技水平高
- 俄罗斯加入世界贸易组织,根本目的在于 A.为了利用俄罗斯的先进技术为世界的发展作出应有的贡献B.参与规则的制定,实现贸易
- 【2016·山东省济南卷】 下列句子中加点成语使用恰当的一项是( ) A. “趵突腾空”为“济南八景”之首,泉水日夜
- 2005年7月,我国辽宁沈阳市新民市大民屯镇突发炭疽病疫情。炭疽热病是由炭疽芽孢杆菌引起的一种人畜共患的传染病,它可引起
- Howbeautiful Catherine sings! I have never heard a ____ voi
- 观察分析下列数据,寻找规律: 0,,,3,2,,3,……那么第10个数据应是 .
- 下列句子中,没有语病的一句是 () A. 我的皮包里装有
- 1某研究性学习小组欲利用下列装置进行相关气体制取的探究,请你分析并填空。(1)写出图中仪器a、b的名称 a



