高中 数学
已知△ABC的顶点A(2,3),且三条中线交于点G(4,1),则BC边上的中点坐标为( )
A . (5,0)
B . (6,﹣1)
C . (5,﹣3)
D . (6,﹣3)
已知等差数列{an}中,公差d=2,an=11,Sn=35,则a1=( )
A . 5或7
B . 3或5
C . 7或﹣1
D . 3或﹣1
已知抛物线y2=4x,其焦点坐标是( )
A . (1,0)
B . (0,1)
C . (-1,0)
D . (0,-1)
如果点(n,an)(n∈N*)都在直线3x-y-24=0上,那么在数列{an}中有( )
A . a7+a9>0
B . a7+a9<0
C . a7+a9=0
D . a7a9=0
已知二次函数  满足下表所给对应关系:
满足下表所给对应关系:
 满足下表所给对应关系:
满足下表所给对应关系: | | 1 | 2 | 4 |
| | 0 | | 0 |
则不等式  的解集为.
的解集为.
若动点  分别在直线
分别在直线  和
和  上,则
上,则  的中点
的中点  到坐标原点的距离的最小值为( )
到坐标原点的距离的最小值为( )
 分别在直线
分别在直线  和
和  上,则
上,则  的中点
的中点  到坐标原点的距离的最小值为( )
到坐标原点的距离的最小值为( )
A .  B .
B .  C .
C . 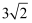 D .
D . 
 B .
B .  C .
C . 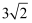 D .
D . 
如图,已知在三棱柱 中,
中, ,
,  , F是线段BC的中点,点O在线段AF上,
, F是线段BC的中点,点O在线段AF上, , D是侧棱
, D是侧棱 中点,
中点, .
.
 中,
中, ,
,  , F是线段BC的中点,点O在线段AF上,
, F是线段BC的中点,点O在线段AF上, , D是侧棱
, D是侧棱 中点,
中点, .
.
-
(1) 证明:

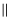 平面
平面 ;
;
-
(2) 若
 , 点
, 点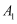 在平面ABC内的射影为O,求直线OE与平面
在平面ABC内的射影为O,求直线OE与平面 所成角的正弦值.
所成角的正弦值.
已知抛物线  的焦点为
的焦点为  ,
,  为该抛物线上一点,若以
为该抛物线上一点,若以  为圆心的圆与
为圆心的圆与  的准线相切于点
的准线相切于点  ,
,  ,过
,过  且与
且与  轴垂直的直线
轴垂直的直线  与
与  交于
交于  ,
,  两点,
两点, 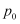 为
为  的准线上的一点,则
的准线上的一点,则  的面积为( )
的面积为( )
 的焦点为
的焦点为  ,
,  为该抛物线上一点,若以
为该抛物线上一点,若以  为圆心的圆与
为圆心的圆与  的准线相切于点
的准线相切于点  ,
,  ,过
,过  且与
且与  轴垂直的直线
轴垂直的直线  与
与  交于
交于  ,
,  两点,
两点, 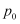 为
为  的准线上的一点,则
的准线上的一点,则  的面积为( )
的面积为( )
A . 1
B . 2
C . 4
D . 8
若扇形的圆心角为 , 半径为6,则该扇形的面积为.
, 半径为6,则该扇形的面积为.
 , 半径为6,则该扇形的面积为.
, 半径为6,则该扇形的面积为.
执行如图所示的程序框图,输入x=﹣1,n=5,则输出s=( )

A . ﹣2
B . ﹣3
C . 4
D . 3
已知i是虚数单位,  =2i,则|z|等于( )
=2i,则|z|等于( )
 =2i,则|z|等于( )
=2i,则|z|等于( )
A . 1
B .  C .
C .  D .
D . 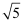
 C .
C .  D .
D . 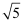
复数 (i是虚数单位)的共轭复数是( )
(i是虚数单位)的共轭复数是( )
 (i是虚数单位)的共轭复数是( )
(i是虚数单位)的共轭复数是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知数列  的通项公式是
的通项公式是  ,前
,前  项和为
项和为  ,则数列
,则数列  的前11项和为( )
的前11项和为( )
 的通项公式是
的通项公式是  ,前
,前  项和为
项和为  ,则数列
,则数列  的前11项和为( )
的前11项和为( )
A . -45
B . -50
C . -55
D . -66
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥PABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥PABC的四个顶点都在球O的球面上,则球O的表面积为( )

A . 8π
B . 12π
C . 20π
D . 24π
如果球的大圆周长为C,则这个球的表面积是( )
A .  B .
B .  C .
C .  D .
D . 
 展开式中
展开式中 的系数为.
的系数为.
已知向量![]()
![]()
![]()
![]() ,
, ![]()
![]() 分别为△ABC的三边
分别为△ABC的三边![]() 所对的角.
所对的角.
(Ⅰ)求角C的大小;
(Ⅱ)若sinA, sinC, sinB成等比数列, 且![]() , 求c的值
, 求c的值
直线l:y=k(x-![]() )与曲线x2-y2=1(x>0)相交于A,B两点,则直线l的倾斜角的取值范围是________________.
)与曲线x2-y2=1(x>0)相交于A,B两点,则直线l的倾斜角的取值范围是________________.
在锐角![]() 中,
中,![]() ,则
,则![]() 的取值范围是 。
的取值范围是 。
若函数 



A . 

C . 

最近更新
- 有一道竞赛题,甲解出它的概率为,乙解出它的概率为,丙解出它的概率为,则甲、乙、丙三人独立解答此题,只有1人解出的概率是(
- 关于意识的本质问题,唯心主义的错误在于 A. 否认意识对物质的决定作用 B. 夸大物质决定意识的作用 C. 否认意识对物
- 已知sinθ=,cosθ=,其中θ∈[],则下列结论正确的是()A. m∈[3,9] B. m∈(﹣∞,5)∪[3,+∞
- In a time of social reform, people’s state of mind tends to
- 对下列句中加点词的解释不正确的一项是 A.长不满七尺,滑稽多辩 滑稽:形容口齿流利,圆转自如。B.先生少之乎
- 在直角坐标系中,已知△ABC三个顶点的坐标分别是 A(0,),B(-1,0),C(1,0),则∠ABC的度数为 °
- 把方程化成的形式,则m、n的值是( ) A、4,13 B、-4,19 C、-4,1
- 2010年6月11日﹣﹣7月11日举行的南非世界杯给无数的球迷留下多个充满激情的时刻.下列关于足球运动所包含的生物学知识
- Barefoot Traveler is a tour operator that specialises in div
- 石家庄市形成和发展的区位因素是( ) ①铁路运输的发展 ②河流干流
- 2009年8月14日起,公安部在全国全面开展整治酒后驾驶交通违法行为专项行动。醉酒驾车者的做法①是尊重他人的行为②是对自
- 20. 某学校生物兴趣小组用伊乐藻进行光合作用的实验,将一枝伊乐藻侵在加有适宜培养液的大试管中,以白炽灯作为光源,移动白
- 14.阅读下面的文字,根据要求作文。 作为一种道德修养,“慎独”最早见于《礼记》,它说:“莫显乎微,故君子慎独也。”东汉
- (江苏省黄桥中学2010届高三上学期期中考试)下列各句中,没有语病的一句是 A.面对席卷全球的金融危机,中国政府紧紧围绕
- 下列关于实验基本操作的叙述中,正确的是 A.胶头滴管加液结束时后,不能倒置,也不能平放于桌面上 B.加热试管里的药品时,
- 唐卡是藏族文化中独具特色的绘画艺术形成,题材内容涉及藏族的历史、政治、文化和社会生活等诸多领域,堪称藏民族的百科全书。它
- 近年来,我国“悟空”暗物质探测卫星、“墨子”量子实验卫星、“慧眼”硬X射线调制望远镜、“太极一号”空间引力波探测卫星等,
- — Catherine, I have cleaned the room for you.— Thanks. You
- 如图所示是银杏树上结的“白果”,对白果是银杏种子的描述正确的是A.成熟时果皮脱落 B.没有果皮包
- ,雪上空留马行处。




