高中 数学
已知函数f(x)=x2﹣6x+7,x∈[1,4],

-
(1) 在给定直角坐标系中画出函数的大致图象;(每个小正方形边长为一个单位长度)
-
(2) 由图象指出函数f(x)的单调递增区间(不要求证明);
-
(3) 由图象指出函数f(x)的值域(不要求证明).
与向量 平行的一个向量的坐标是 ( )
平行的一个向量的坐标是 ( )
 平行的一个向量的坐标是 ( )
平行的一个向量的坐标是 ( )
A . ( ,1,1)
B . (-1,-3,2)
C . (-
,1,1)
B . (-1,-3,2)
C . (- ,
, ,-1)
D . (
,-1)
D . ( ,-3,-2
,-3,-2 )
)
 ,1,1)
B . (-1,-3,2)
C . (-
,1,1)
B . (-1,-3,2)
C . (- ,
, ,-1)
D . (
,-1)
D . ( ,-3,-2
,-3,-2 )
)
某正弦交流电的电压v(单位V)随时间t(单位:s)变化的函数关系是v=120  sin(100πt﹣
sin(100πt﹣  ),t∈[0,+∞).
),t∈[0,+∞).
 sin(100πt﹣
sin(100πt﹣  ),t∈[0,+∞).
),t∈[0,+∞).
-
(1) 求该正弦交流电电压v的周期、频率、振幅;
-
(2) 若加在霓虹灯管两端电压大于84V时灯管才发光,求在半个周期内霓虹灯管点亮的时间?( 取
 ≈1.4)
≈1.4)
等比数列  的前
的前  项和为
项和为  ,若
,若  ,
,  ,
,  ,
,  ,则
,则  ( )
( )
 的前
的前  项和为
项和为  ,若
,若  ,
,  ,
,  ,
,  ,则
,则  ( )
( )
A .  B .
B . 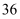 C .
C .  D .
D . 
 B .
B . 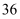 C .
C .  D .
D . 
求两条垂直的直线2x+y+2=0与ax﹣y﹣2=0的交点坐标.
已知集合  ,
,  ,
,  ,则
,则  ( ).
( ).
 ,
,  ,
,  ,则
,则  ( ).
( ).
A . {-1}
B . {1}
C .  D .
D . 
 D .
D . 
已知椭圆C:  =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 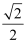 ,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为
,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为  +1
+1
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 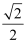 ,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为
,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为  +1
+1 (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线L的斜率为k,且过左焦点F1 , 与椭圆C相交于P、Q两点,若△PQF2的面积为  ,试求k的值及直线L的方程.
,试求k的值及直线L的方程.
设集合M={x|x=3k,k∈Z},P={x|x=3k+1,k∈Z},Q={x|x=3k-1,k∈Z},若a∈M,b∈P,c∈Q,则a+b-c∈.
如果偶函数  在区间
在区间  上有最大值M , 那么
上有最大值M , 那么  在区间
在区间  上( )
上( )
 在区间
在区间  上有最大值M , 那么
上有最大值M , 那么  在区间
在区间  上( )
上( )
A . 有最小值M
B . 没有最小值
C . 有最大值M
D . 没有最大值
已知两点  到直线l的距离等于a,且这样的直线l可作4条,则a的取值范围是.
到直线l的距离等于a,且这样的直线l可作4条,则a的取值范围是.
 到直线l的距离等于a,且这样的直线l可作4条,则a的取值范围是.
到直线l的距离等于a,且这样的直线l可作4条,则a的取值范围是.
已知正方体  的棱长为2,
的棱长为2,  为棱
为棱  的中点,截面
的中点,截面  交棱
交棱  于点
于点  ,则四面体
,则四面体  的外接球表面积为( )
的外接球表面积为( )
 的棱长为2,
的棱长为2,  为棱
为棱  的中点,截面
的中点,截面  交棱
交棱  于点
于点  ,则四面体
,则四面体  的外接球表面积为( )
的外接球表面积为( )
A .  B .
B .  C . 12π
D .
C . 12π
D . 
 B .
B .  C . 12π
D .
C . 12π
D . 
从2020年元月份以来,全世界的经济都受到了新冠病毒的严重影响,我国抗疫战斗取得了重大的胜利,全国上下齐心协力复工复产,抓经济建设;某公司为了提升市场的占有率,准备对一项产品实施科技改造,经过充分的市场调研与模拟,得到  ,
,  之间的五组数据如下表:
之间的五组数据如下表:
 ,
,  之间的五组数据如下表:
之间的五组数据如下表:
|
|
2 |
3 |
5 |
7 |
8 |
|
|
5 |
8 |
12 |
14 |
16 |
其中,  (单位:百万元)是科技改造的总投入,
(单位:百万元)是科技改造的总投入,  (单位:百万元)是改造后的额外收益;设
(单位:百万元)是改造后的额外收益;设  是对当地生产总值增长的贡献值.
是对当地生产总值增长的贡献值.
附:对于一组数据  ,其拟合直线方程
,其拟合直线方程  的残差平方和为
的残差平方和为  ,
,  越小拟合效果越好.
越小拟合效果越好.
-
(1) 若从五组数据中任取两组,求恰有一组满足
 的概率;
的概率;
-
(2) 记
 为
为  时的任意两组数据对应的贡献值的和,求随机变量
时的任意两组数据对应的贡献值的和,求随机变量  的分布列和数学期望;
的分布列和数学期望;
-
(3) 利用表中数据,甲、乙两个调研小组给出的拟合直线方程分别为甲组:
 ,乙组:
,乙组:  ,试用最小二乘法判断哪条直线的拟合效果更好?
,试用最小二乘法判断哪条直线的拟合效果更好?
等差数列  的前
的前  项和记为
项和记为  ,若
,若  ,则
,则  ( )
( )
 的前
的前  项和记为
项和记为  ,若
,若  ,则
,则  ( )
( )
A . 6:1
B . 1:5
C . 1:6
D . 5:1
某大学志愿者协会有6名男同学,4名女同学,在这10名同学中,3名同学来自数学学院,其余7名同学来自物理﹑化学等其他互不相同的七个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
-
(1) 求选出的3名同学是来自互不相同学院的概率;
-
(2) 设
 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量  的分布列.
的分布列.
已知cosθ=﹣  ,θ∈(π,
,θ∈(π,  ),求tan(θ﹣
),求tan(θ﹣  )的值.
)的值.
 ,θ∈(π,
,θ∈(π,  ),求tan(θ﹣
),求tan(θ﹣  )的值.
)的值.
复数  在复平面内对应的点为
在复平面内对应的点为  ,则
,则  ( )
( )
 在复平面内对应的点为
在复平面内对应的点为  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在三棱锥S―ABC中,△ABC是边长为4的正三角形,SB=![]() ,SA=SC=
,SA=SC=![]() ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(I)证明:平面SAC⊥平面ABC;
(II)求MN与平面SBC所成角的正弦值。

在△ABC中,点E满足![]() ,且
,且![]() ,则m﹣n=( )
,则m﹣n=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知椭圆![]() F1、F2为焦点,Q为椭圆上任意一点,过F2作∠F1QF2补角平分线的垂线,垂足为N,(如图)则Q点在椭圆上运动时,点N的运动轨迹
F1、F2为焦点,Q为椭圆上任意一点,过F2作∠F1QF2补角平分线的垂线,垂足为N,(如图)则Q点在椭圆上运动时,点N的运动轨迹

20080528
A.线段 B.圆 C.椭圆 D.双曲线
等差数列![]() ,
,![]() ,
,![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 达到最大值.
达到最大值.
A.8 B.7 C. 6 D. 9
最近更新
- 阅读理解 阅读下面的短文,根据短文内容,从每题所给的A、B、C、D四个选项中选出最佳答案。 Studying in gr
- 在由水电离产生的H浓度为l×10mol・L的溶液中,一定能大量共存的离子组是( ) ①K、Cl、NO、S ②K、
- 在进行光学实验的探究过程中:(1)小明同学用如上图所示的装置,研究光的反射规律,其中用到了一个可折转的光屏,这个光屏在实
- 武则天于684年下令:凡官吏所在地区,“田畴垦辟,家有余粮”者升官。这体现了武则天 A.严惩贪官污吏 B
- 阅读下面一首宋词,然后回答问题。 蝶恋花 欧阳修 庭院深深深几许?杨柳堆烟,帘幕无重数。玉勒雕鞍游冶处,楼高不见章台路。
- 甲、乙两人对同一目标各射击一次,甲命中目标的概率为,乙命中目标的概率为,若命中目标的人数为,则__________.
- Lucy and Lily are twin sisters.But Lucy is ______ than Lily.
- 生活在高原上的人们,血液中的红细胞数量较多,出现此生理现象的主要原因是下列哪种生态因素造成的( ) A.空气
- 常见的河流堆积地貌有 A.河流阶地、大峡谷 B.河口三角洲、冲积扇 C.喀斯特地貌、陡崖 D.角峰、U型冰川谷
- 下列各数中,3.14159,,0.131131113……,-π,,,无理数的个数有 .1个 .2个 .
- 下表为19世纪50年代初中国与美国、印度钢和发电(人均)产量方面的比较表为能使中国自立于世界民族之林,我国采取的相应措施
- 下列物质中的少量杂质(括号内为杂质),只需适量NaOH的固体或溶液就能除去的是( ) A.CO2 (H2O
- A、B、C、D四个完全相同的小球等间距地分布在一条竖直直线上,相邻两球的距离等于A球到地面的距离.现让四球以相同的水平速
- 2.下列各项中,没有语病的一项是 A.全球最快的轿车车型问世!奔驰官方改装商Brabus声称,其基于奔驰顶级轿车S级打造
- 现代服务业具有智力型、技术型、知识产权化和高附加值的特征。据统计,服务业每万元增加值的用电量、占有资本分配约为工业的15
- 一个边长为L,匝数为n的正方形线圈,在匀强磁场中从中性面开始绕中心轴匀速转动,角速度为ω,磁场的磁感强度为B,这个线圈中
- 如图所示, (1)写出图中装置的仪器名称:a b (2)若用此发生装置制取氧气时,往a中加入适量的 溶液至使a
- Along with the letter was his promise ________ he would visi
- 古诗“花气袭人知骤暖”, 从花的芳香气味变浓可以知道周边的气温突然升高。从物理学的角度分析,这是因为温度越高,
- 请以“那段日子,我们一起走过”为题写一篇文章。 要求:1、题材不限(诗歌除外),不少于600字 2、文中不得



