高中 数学
-
(1) 计算
 ;
;
-
(2) 在复数范围内解关于x的方程:
 .
.
下列选项中,错误的是( )
A . 若p为真,则¬(¬p)也为真
B . 若“p∧q为真”,则“p∨q为真”为真命题
C . ∃x∈R,使得tanx=2017
D . “2x>  ”是“log
”是“log  x<0”的充分不必要条件
x<0”的充分不必要条件
 ”是“log
”是“log  x<0”的充分不必要条件
x<0”的充分不必要条件
在平面直角坐标系  中,双曲线
中,双曲线  的渐近线方程是( )
的渐近线方程是( )
 中,双曲线
中,双曲线  的渐近线方程是( )
的渐近线方程是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某市出租车收费标准如下:起步价8元,起步里程为3km(不超过3km按起步价付费);超过3km但不超过8km时,超过部分按每千米2.15元收费;超过8km时,超过部分按每千米2.85元收费;另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费31.15元,则此次出租车行驶了km.
已知函数 的导函数
的导函数 , 且满足
, 且满足 , 求
, 求 =( )
=( )
 的导函数
的导函数 , 且满足
, 且满足 , 求
, 求 =( )
=( )
A . 1
B . -1
C . - D .
D . 
 D .
D . 
已知函数  .
.
 .
.
-
(1) 求曲线
 在点
在点  ,
,  处的切线方程;
处的切线方程;
-
(2) 求
 在
在  ,
,  上的最大值和最小值.
上的最大值和最小值.
已知点  ,
,  是抛物线
是抛物线  的焦点,
的焦点,  是抛物线上的动点,当
是抛物线上的动点,当  最小时,
最小时,  点坐标是.
点坐标是.
 ,
,  是抛物线
是抛物线  的焦点,
的焦点,  是抛物线上的动点,当
是抛物线上的动点,当  最小时,
最小时,  点坐标是.
点坐标是.
已知函数 的图象和直线
的图象和直线 有三个交点,则
有三个交点,则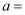 .
.
 的图象和直线
的图象和直线 有三个交点,则
有三个交点,则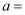 .
.
与cos50°cos20°+sin50°sin20°相等的是( )
A . cos30°
B . sin30°
C . cos70°
D . sin70°
已知 
 为椭圆
为椭圆  上一点,
上一点,  分别为
分别为  关于
关于  轴,原点,
轴,原点,  轴的对称点,
轴的对称点,

 为椭圆
为椭圆  上一点,
上一点,  分别为
分别为  关于
关于  轴,原点,
轴,原点,  轴的对称点,
轴的对称点,
-
(1) 求四边形
 面积的最大值;
面积的最大值;
-
(2) 当四边形
 最大时,在线段
最大时,在线段  上任取一点
上任取一点  ,若过
,若过  的直线与椭圆相交于
的直线与椭圆相交于  两点,且
两点,且  中点恰为
中点恰为  ,求直线
,求直线  斜率
斜率  的取值范围.
的取值范围.
如图,直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AB=2,BC=1,D为AB中点,则异面直线CD与A1C1所成的角的大小为( )

A . 90°
B . 60°
C . 45°
D . 30°
已知点  是角
是角  终边上一点,则
终边上一点,则  的值为( )
的值为( )
 是角
是角  终边上一点,则
终边上一点,则  的值为( )
的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设P是不等式组  表示的平面区域内的任意一点,向量
表示的平面区域内的任意一点,向量  =(1,1),
=(1,1),  =(2,1),若
=(2,1),若  =λ
=λ  +μ
+μ  (λ,μ为实数),则λ﹣μ的最大值为( )
(λ,μ为实数),则λ﹣μ的最大值为( )
 表示的平面区域内的任意一点,向量
表示的平面区域内的任意一点,向量  =(1,1),
=(1,1),  =(2,1),若
=(2,1),若  =λ
=λ  +μ
+μ  (λ,μ为实数),则λ﹣μ的最大值为( )
(λ,μ为实数),则λ﹣μ的最大值为( )
A . 4
B . 3
C . ﹣1
D . ﹣2
若将整个样本空间想象成一个1×1的正方形,任何事件都对应样本空间的一个子集,且事件发生的概率对应子集的面积.则如图所示的涂色部分的面积表示( )

A . 事件A发生的概率
B . 事件B发生的概率
C . 事件B不发生条件下事件A发生的概率
D . 事件A、B同时发生的概率
在锐角  中,角
中,角  、
、  、
、  所对的边分别为
所对的边分别为  、
、  、
、  ,已知
,已知  .
.
 中,角
中,角  、
、  、
、  所对的边分别为
所对的边分别为  、
、  、
、  ,已知
,已知  .
. (Ⅰ)求证  ;
;
(Ⅱ)求  的取值范围.
的取值范围.
已知函数  ,若函数
,若函数  恰有三个零点,则实数
恰有三个零点,则实数  的取值范围是.
的取值范围是.
 ,若函数
,若函数  恰有三个零点,则实数
恰有三个零点,则实数  的取值范围是.
的取值范围是.
命题:  的否定是.
的否定是.
 的否定是.
的否定是.
直线 被圆
被圆 所截的弦长为.
所截的弦长为.
 被圆
被圆 所截的弦长为.
所截的弦长为.
已知全集U=Z,A={-1,0,1,2},B={x|x2=x},则A![]() (CUB)=_____________.
(CUB)=_____________.
命题P:“若![]() ,则a、b、c成等比数列”,则命题P的否命题是 (填“真”或“假”之一)命题.
,则a、b、c成等比数列”,则命题P的否命题是 (填“真”或“假”之一)命题.
最近更新
- 20℃时硫酸的密度和溶质质量分数对照表:密度(克/厘米3) 1.07 1.14 1.30 1.50 1.73 1.84
- 用NA表示阿伏加德罗常数的数值,下列说法中不正确的是() A.常温下,1 L pH=3的硫酸中,SO的数目约为5×10-
- 23.在下面一段文字横线处补写恰当的语句,使整段文字语意完整连贯,内容贴切,逻辑严密。每处不超过12个字。 今天为什么还
- 已知f(x)=sinx+cosx(x∈R),函数y=f(x+φ)的图象关于直线x=0对称,则φ的值可以是() (A)
- 阅读材料,回答问题。 材料一: 材料二:据统计,占人口10%的最高收入群体和收入最低的10%群体的收入差距已从1988年
- 下列叙述不正确的是() A.太阳能蓄电池只是将太阳能直接转化为电能的装置 B.燃料电池是将化学能直接转化为电能的装置,所
- 活的细胞,细胞膜能够让有用的物质进入细胞,把其他物质挡在细胞外,同时,还能把细胞内产生的废物排出体外,而又不让细胞内有用
- 下列各句中,加点词语能被括号中的词语替换且符合句意的一项是( ) A.针对个别干部违规驾驶公车发生交通事故的现象
- —Let's _________ volleyball. —_____________. A.playing;That
- (10分)室常用的实验装置,回答问题: (1)写出带有标号仪器的名称:① ;② 。(2
- Recently Iexperienced a wonderful lesson in how little thing
- 下列事实一定能说明HF是弱酸的是( ) ①常温下NaF溶液的pH大于7; ②用HF溶液做导电性实验,灯泡很暗;
- 在研究光照强度对某种鸟鸣叫次数的影响中,下列设计不符合研究要求的是 A.记录一天内不同时间同一地点该种鸟鸣叫次数 B.记
- 蒹葭苍苍, 。(《诗经·蒹葭》)
- 下面一段话画线的句子中六句有语病,请选出四句加以修改。 ①节食和强制限食,并非与肥胖做斗争的好办法,②重要的是选择科学的
- 6.如图5所示,描述不正确的是:
- 为了预防碘缺乏病,国家规定每千克食盐中应含有40—50 mg的碘酸钾。为检验某种食盐是否为加碘的合格食盐,某同学取食盐样
- Li Hua's house is very far.She ______ the subway to school e
- 阅读下面一首唐诗,然后回答问题。 宿甘露寺 曾公亮 枕中云气千峰近,床底松声万壑哀。 要看银海拍天浪,开窗放入大江来。
- 浠州县为了改善全县中、小学办学条件,计划集中采购一批电子白板和投影机,已知购买2块电子白板比购买3台投影机多4000元,



