高中 数学
求下列各式x的取值范围.
-
(1) log(x﹣1)(x+2);
-
(2) log(x+3)(x+3).
已知函数  的定义域是一切实数,则
的定义域是一切实数,则  的取值范围是( )
的取值范围是( )
 的定义域是一切实数,则
的定义域是一切实数,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
两个半径都是  的球
的球 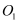 和球
和球  相切,且均与直二面角
相切,且均与直二面角  的两个半平面都相切,另有一个半径为1的小球
的两个半平面都相切,另有一个半径为1的小球  与这二面角的两个半平面也都相切,同时与球
与这二面角的两个半平面也都相切,同时与球 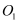 和球
和球  都外切,则
都外切,则  的值为
的值为 

 的球
的球 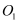 和球
和球  相切,且均与直二面角
相切,且均与直二面角  的两个半平面都相切,另有一个半径为1的小球
的两个半平面都相切,另有一个半径为1的小球  与这二面角的两个半平面也都相切,同时与球
与这二面角的两个半平面也都相切,同时与球 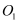 和球
和球  都外切,则
都外切,则  的值为
的值为 

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某几何体的三视图如图所示(单位: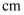 ),则该几何正视图体的表面积(单位:
),则该几何正视图体的表面积(单位: )是( )
)是( )
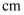 ),则该几何正视图体的表面积(单位:
),则该几何正视图体的表面积(单位: )是( )
)是( )
A . 17
B . 18
C . 19
D . 20
数列{an}的前n项和Sn满足Sn=  +An,若a2=2,则A=,数列
+An,若a2=2,则A=,数列  的前n项和Tn=.
的前n项和Tn=.
 +An,若a2=2,则A=,数列
+An,若a2=2,则A=,数列  的前n项和Tn=.
的前n项和Tn=.
椭圆C: , (a>b>0)的离心率
, (a>b>0)的离心率 , 点(2,
, 点(2, )在C上.
)在C上.
 , (a>b>0)的离心率
, (a>b>0)的离心率 , 点(2,
, 点(2, )在C上.
)在C上.(1)求椭圆C的方程;
(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与l的斜率的乘积为定值.
已知倾斜角为  的直线l的斜率等于双曲线
的直线l的斜率等于双曲线  的离心率,则
的离心率,则  =.
=.
 的直线l的斜率等于双曲线
的直线l的斜率等于双曲线  的离心率,则
的离心率,则  =.
=.
已知集合  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知物体的运动方程是 (
( 表示时间,
表示时间, 表示位移),则瞬时速度为0的时刻是( )
表示位移),则瞬时速度为0的时刻是( )
 (
( 表示时间,
表示时间, 表示位移),则瞬时速度为0的时刻是( )
表示位移),则瞬时速度为0的时刻是( )
A . 0秒、2秒或4秒
B . 0秒、2秒或16秒
C . 2秒、8秒或16秒
D . 0秒、4秒或8秒
等比数列  的前
的前  项和为
项和为  ,若
,若  ,则
,则  的值为( )
的值为( )
 的前
的前  项和为
项和为  ,若
,若  ,则
,则  的值为( )
的值为( )
A . -3
B . -1
C . 1
D . 3
已知椭圆 
 ,
,  、
、  为
为  的左、右焦点.
的左、右焦点.

 ,
,  、
、  为
为  的左、右焦点.
的左、右焦点.
-
(1) 求椭圆
 的焦距;
的焦距;
-
(2) 点
 为椭圆
为椭圆  一点,与
一点,与  平行的直线
平行的直线  与椭圆
与椭圆  交于两点A、B,若
交于两点A、B,若  面积为
面积为  ,求直线
,求直线  的方程;
的方程;
-
(3) 已知椭圆
 与双曲线
与双曲线  在第一象限的交点为
在第一象限的交点为  ,椭圆
,椭圆  和双曲线
和双曲线  上满足
上满足  的所有点
的所有点  组成曲线
组成曲线  .若点
.若点  是曲线
是曲线  上一动点,求
上一动点,求  的取值范围.
的取值范围.
已知全集A={x∈N|x<2},B={0,1,2},则A∩B=( )
A . {1,2}
B . {0,1,2}
C . {1}
D . {0,1}
若实数 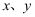 满足
满足  ,则
,则  的最大值为。
的最大值为。
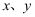 满足
满足  ,则
,则  的最大值为。
的最大值为。
在锐角三角形 中,角
中,角 ,
,  ,
,  的对边分别为
的对边分别为 ,
,  ,
,  , 若
, 若 , 则
, 则 的取值范围是( )
的取值范围是( )
 中,角
中,角 ,
,  ,
,  的对边分别为
的对边分别为 ,
,  ,
,  , 若
, 若 , 则
, 则 的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PAL底面ABCD,且PA=AB.

-
(1) 求证:BD⊥平面PAC;
-
(2) 求异面直线BC与PD所成的角.
若向量 ,
,  , 下列结论正确的是( )
, 下列结论正确的是( )
 ,
,  , 下列结论正确的是( )
, 下列结论正确的是( )
A . 若 同向,则
同向,则 B . 与
B . 与 垂直的单位向量一定是
垂直的单位向量一定是 C . 若
C . 若 在
在 上的投影向量为
上的投影向量为 (
( 是与向量
是与向量 同向的单位向量),则
同向的单位向量),则 D . 若
D . 若 与
与 所成角为锐角,则n的取值范围是
所成角为锐角,则n的取值范围是
 同向,则
同向,则 B . 与
B . 与 垂直的单位向量一定是
垂直的单位向量一定是 C . 若
C . 若 在
在 上的投影向量为
上的投影向量为 (
( 是与向量
是与向量 同向的单位向量),则
同向的单位向量),则 D . 若
D . 若 与
与 所成角为锐角,则n的取值范围是
所成角为锐角,则n的取值范围是
在平面直角坐标系内,已知![]() ,
,![]() ,
,![]() ;
;
(1)当![]() 时,求直线
时,求直线![]() 的倾斜角
的倾斜角![]() 的取值范围;
的取值范围;
(2)当![]() 时,求
时,求![]() 的
的![]() 边上的高
边上的高![]() 所在直线方程.
所在直线方程.
设数列{![]() }的前n项和
}的前n项和![]() 满足:
满足:![]() =n
=n![]() -2n(n-1).等比数列{
-2n(n-1).等比数列{![]() }的前n项和为
}的前n项和为![]() ,公比为
,公比为![]() ,且
,且![]() =
=![]() +2
+2![]() .
.
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设数列{![]() }的前n项和为
}的前n项和为![]() ,求证:
,求证:![]() ≤
≤![]() <
<![]() .
.
若不等式![]() 对于一切非零实数x均成立,则实数
对于一切非零实数x均成立,则实数![]() 的取值范围是
的取值范围是
A. [-1,1] B. ![]() C. (-2,2) D.[-2,2]
C. (-2,2) D.[-2,2]
已知α是第二象限角,tan(π-α)= ![]() ,则tanα=______ __.
,则tanα=______ __.
最近更新
- 下列地理现象按其因果关系排列,正确的是() A.工业联系→工业地域→工业集聚→工业城市 B.工业集聚→工业地域→工业
- Na2CO3水溶液中存在CO2-3+H2OHCO-3+OH-平衡。下列说法不正确的是( ) A.稀释溶液,增大
- .命题“存在,为假命题”是命题“”的( ) A.充要条件 B.必要不
- 促使一战迅速结束的主要原因是( ) A.俄国发生“二月革命”和“十月革命”退出帝国主义战争 B.美国参加对德作战
- 已知函数,且,那么等于( ) A 10 B.-10 C.-18 D.-26
- (07年湖南卷理)函数在区间上的最小值是 .
- 重铬酸钾是工业生产和实验室的重要氧化剂,工业上常用铬铁矿(主要成分为FeO·Cr2O3,杂质为SiO2、Al2O3)为原
- 截至2010年3月29日,国务院已经正式批准25个城市建设地铁。按照规划,2010至2015年地铁建设投资额将达11 5
- (本题满分16分) 设函数. (Ⅰ) 判断在区间上的增减性并证明之; (Ⅱ) 若不等式≤≤对恒成立, 求实数的取值范围M
- 关于振动和波的关系下列叙述中正确的是 ( )A.有机械振动,就一定能形成机械波B.有机械波
- 在完全显性的条件下,AaBbCc与aaBbcc的个体杂交(符合独立分配规律),其子代表现型不同于双亲的个体占子代的(
- 下列卤代烃既属于芳香族卤代烃,又属于二卤代烃的是( )
- 3.依次填入下面一段文字横线处的语句,衔接最恰当的一组是(3分) 物的崇拜从来是与富贵、炫耀和时尚密切关联的。_____
- 下列各句中,加点的成语使用恰当的一项是(3分) ( ) A.12月2日,湖南茶业博览会在省展览馆举行。这次博览会
- 下列化学用语表达正确的是( ) A. 3个钠离子-- B. 2个氧原子--O2 C.
- 图中画出手对扳手的动力F的力臂,井用字母L表示.
- TODAY, Friday, November 12JAZZ with the Mike Thomas Jazz Ban
- 对于“9.11”恐怖事件,国际有关专家认为:“美国政府宁愿用100万美元的导弹轰炸不值十美元一顶的帐篷,坚持出兵阿富汗,
- 海水淡化可采用膜分离技术.如图所示,对淡化膜右侧的海水加压,水分子可以透过淡化膜进入淡水池,而海水中的各种溶质不能通过淡
- 先阅读短文,掌握其大意。然后从方框中所给的词中选出恰当的10个,并用其适当形式填空,每个词限用一次。(每小题1分) st



