高中 数学
为了让居民了解垃圾分类,养成垃圾分类的习惯,让绿色环保理念深入人心.某市将垃圾分为四类可回收物,餐厨垃圾,有害垃圾和其他垃圾.某班按此四类由9位同学组成四个宣传小组,其中可回收物宣传小组有3位同学,餐厨垃圾、有害垃圾和其他垃圾宣传小组各有2位同学.现从这9位同学中选派5人到某小区进行宣传活动,则每个宣传小组至少选派1人的概率为( )
A . 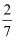 B .
B . 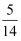 C .
C . 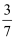 D .
D . 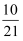
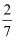 B .
B . 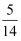 C .
C . 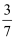 D .
D . 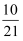
设△ABC的内角A,B,C所对的边分别为a,b,c,若acosB+bcosA=csinC,则△ABC的形状为( )
A . 锐角三角形
B . 等腰直角三角形
C . 钝角三角形
D . 直角三角形
已知函数  是定义在
是定义在  上的奇函数,且当
上的奇函数,且当  时,
时,  ;
;
 是定义在
是定义在  上的奇函数,且当
上的奇函数,且当  时,
时,  ;
;
-
(1) 求函数
 在
在  上的解析式;
上的解析式;
-
(2) 是否存在非负实数
 ,使得当
,使得当  时,函
时,函  的值域为
的值域为  ?若存在,求出所有
?若存在,求出所有  的值;若不存在,说明理由.
的值;若不存在,说明理由.
《算数书》是我国现存最早的系统性数学典籍,其中记载有求“困盖”的术:置如其周,令相乘也,又以高乘之,三十六成一,该术相当于给出了由圆锥的底面周长  与高
与高  ,计算其体积
,计算其体积 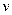 的近似公式
的近似公式 
 ,用该术可求得圆周率
,用该术可求得圆周率  的近似值.现用该术求得
的近似值.现用该术求得  的近似值,并计算得一个底面直径和母线长相等的圆锥的表面积的近似值为9,则该圆锥体积的近似值为( )
的近似值,并计算得一个底面直径和母线长相等的圆锥的表面积的近似值为9,则该圆锥体积的近似值为( )
 与高
与高  ,计算其体积
,计算其体积 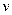 的近似公式
的近似公式 
 ,用该术可求得圆周率
,用该术可求得圆周率  的近似值.现用该术求得
的近似值.现用该术求得  的近似值,并计算得一个底面直径和母线长相等的圆锥的表面积的近似值为9,则该圆锥体积的近似值为( )
的近似值,并计算得一个底面直径和母线长相等的圆锥的表面积的近似值为9,则该圆锥体积的近似值为( )
A .  B . 2
B . 2  C . 3
C . 3  D . 3
D . 3
 B . 2
B . 2  C . 3
C . 3  D . 3
D . 3
等差数列 和
和 的前n项和分别为
的前n项和分别为 和
和 , 且
, 且 , 则
, 则 ( )
( )
 和
和 的前n项和分别为
的前n项和分别为 和
和 , 且
, 且 , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,已知 是抛物线
是抛物线 的焦点,点
的焦点,点 是抛物线
是抛物线 上一动点,点
上一动点,点 ,
,  的最小值为
的最小值为 .
.
 是抛物线
是抛物线 的焦点,点
的焦点,点 是抛物线
是抛物线 上一动点,点
上一动点,点 ,
,  的最小值为
的最小值为 .
.
-
(1) 求抛物线
 的标准方程;
的标准方程;
-
(2) 过直线
 上一动点
上一动点 作抛物线
作抛物线 的两条切线
的两条切线 、
、 , 切点分别为
, 切点分别为 、
、 , 证明:直线
, 证明:直线 过定点.
过定点.
已知函数  的图象在
的图象在 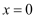 和
和  处的切线互相垂直,则
处的切线互相垂直,则  .
.
 的图象在
的图象在 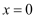 和
和  处的切线互相垂直,则
处的切线互相垂直,则  .
.
命题“  ,
,  ”的否定是
”的否定是 

 ,
,  ”的否定是
”的否定是 

A . 不存在  ,
,  B . 存在
B . 存在  ,
,  C . 对任意的
C . 对任意的  ,
,  D .
D .  ,
, 
 ,
,  B . 存在
B . 存在  ,
,  C . 对任意的
C . 对任意的  ,
,  D .
D .  ,
, 
某个总体由编号为001,002,…,799,800的800个个体组成,利用下面的随机数表选取50个个体,选取方法是从随机数表第2行的第4列数字开始由左到右依次选取,每行结束后紧接下一行,则选出来的第4个个体的编号为( )
0977931982749480040445073166493326168045
3362468628083154463253941338472707360751
0503272483728944056035803994881355385859
1256859926969668273105037293155712101427
A . 133
B . 325
C . 394
D . 603
椭圆 的焦距为( )
的焦距为( )
 的焦距为( )
的焦距为( )
A . 10
B . 5
C .  D .
D . 
 D .
D . 
已知函数

-
(1) 当
 时,求
时,求 极值.
极值.
-
(2) 设
 为
为 的极值点,证明:
的极值点,证明: .
.
设是各项为正数的无穷数列,Ai是边长为ai , ai+1的矩形面积(i=1,2,...),则{An}为等比数列的充要条件为( )
A . {an}是等比数列。
B . a1 , a3 , ...,a2n-1 , ...或a2 , a4 , ...,a2n , ...是等比数列。
C . a1 , a3 , ...,a2n-1 , ...和a2 , a4 , ...,a2n , ...均是等比数列。
D . a1 , a3 , ...,a2n-1 , ...和a2 , a4 , ...,a2n , ...均是等比数列,且公比相同。
已知函数f(x)的定义域为R,且  ,则不等式
,则不等式  解集为( )
解集为( )
 ,则不等式
,则不等式  解集为( )
解集为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数  的定义域是
的定义域是 

 的定义域是
的定义域是 

A .  B .
B .  C .
C .  D .
D . 
已知函数 的定义域均为R,且
的定义域均为R,且 , 则( )
, 则( )
 的定义域均为R,且
的定义域均为R,且 , 则( )
, 则( )
A . 函数 的图像关于点
的图像关于点 对称
B . 函数
对称
B . 函数 的图像关于点
的图像关于点 对称
C . 函数
对称
C . 函数 的图像关于直线
的图像关于直线 对称
D . 函数
对称
D . 函数 的图像关于直线
的图像关于直线 对称
对称
 的图像关于点
的图像关于点 对称
B . 函数
对称
B . 函数 的图像关于点
的图像关于点 对称
C . 函数
对称
C . 函数 的图像关于直线
的图像关于直线 对称
D . 函数
对称
D . 函数 的图像关于直线
的图像关于直线 对称
对称
函数 在区间
在区间 上的图象为( )
上的图象为( )
 在区间
在区间 上的图象为( )
上的图象为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.
某工厂生产一种机器的固定成本 (即固定投入) ![]() 万元,而每生产一台机器还需要增加可变成本(即工人工资、以及其它消耗等)
万元,而每生产一台机器还需要增加可变成本(即工人工资、以及其它消耗等)![]() 万元,市场对此机器的需求量为500台,销售收入函数为
万元,市场对此机器的需求量为500台,销售收入函数为![]() (单位:万元),其中
(单位:万元),其中![]() 为产品售出的数量(单位:百台)
为产品售出的数量(单位:百台)
(I)写出利润![]() (单位:万元)关于年产量
(单位:万元)关于年产量![]() (单位:百台,
(单位:百台,![]() )的函数关系式;
)的函数关系式;
(II)求年产量为多少时,工厂利润最大,并求出最大值.
已知![]() ,求
,求![]() 的值.
的值.
设 ,则
,则 ( )
( )
A. B. 2 C.
B. 2 C.  D.
D. 
A.
最近更新
- 下列字形全部正确的一项 A.出奇制胜 闲情逸志 莫衷一是 蜕化变质B.名门望族 化为乌有 头昏目眩
- 关于内环境稳态的叙述,不正确的是 A.正常机体通过调节作用,使各个器官、系统协调活动,共同维持内环境的相对稳定状态
- In order to attend the meeting, I think youhad better
- 某星球的半径R′是地球半径R的0.5倍(即R′=0.5R),该星球的质量m′是地球质量m的4倍(即m′=4m),已知在
- 实验室需要 0.1mol/L的 H2SO4溶液980mL,欲用 98%、密度为1.84g/cm3的浓硫酸配制.(1)所需
- (4分)将1 mol I2(g)和2 mol H2置于2L密闭容器中,在一定温度下发生反应: I2(g) + H2(g)
- Lin Qiao is a student of GradeEight. She always works hard
- Prices of daily goods _____ through a computer can be lower
- 14.下列句子中,没.有.语病的一句是 (3 分) A.此次会议发言要求每人五分钟,可轮到王老师,他足足讲了十分钟,罗列
- “今日幸颐和,明日幸北海,何日再幸古长安?……五十割交趾,六十割台湾,七十更割辽东地……”这是革命家章炳麟先生讽刺慈禧
- 太阳表面温度约为6000K,主要发出可见光,人体温度约为310K,主要发出红外线,宇宙间的温度约为3K,所发出的辐射称
- 如图,在直三棱柱中, AB=1,,∠ABC=60. (Ⅰ)证明:; (Ⅱ)求二面角A——B的大小。
- 下列句子中划线的词语使用不正确的一项是(2分)A.近期,把教育界搅得沸沸扬扬的话题,莫过于“中国狼爸”萧百佑了。B.他一
- 在数列中, ,,则数列的通项______.
- 5.下列句子,从特殊句式的角度考虑,不同于其他三项的一项是( ) A.譬若以肉投馁虎,何功之有哉? B.太子及宾客知
- 点P(-3,1)在椭圆=1(a>b>0)的左准线上,过点P且方向为a=(2,-5)的光线经直线y=-2反射后通过椭圆的左
- 有一包不纯的CaCO3样品,其中只含有一种杂质,现取该样品5g与足量稀盐酸反应生成2.3gCO2,则所混杂质可能是(
- 图11漫画《今日武松》体现的哲理是A.实践是认识的目的 B.能指导人们行动的价值观才是正确的C.自然规律不是
- 如图所示,定滑轮的质量和摩擦都可忽略不计,轻绳绕过定滑轮连接着 A、B两个物体,物体A在水平桌面上保持静止,已知A的质量
- All cases children are dealt with in a special children’s c



