高中 数学
为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是( )
 ,θ∈(π,2π),则sinθ=,tan
,θ∈(π,2π),则sinθ=,tan  .
.
 ,
, .
.-
(1) (I)求
 的单调区间和极值;
的单调区间和极值;
-
(2) (II)证明:若
 存在零点,则
存在零点,则 的区间(1,
的区间(1, ]上仅有一个零点。
]上仅有一个零点。

如图所示的小木块中,上面7层为高尔顿板,最下面一层为改造的高尔顿板,小球从通道口落下,第一次与第2层中间的小木块碰撞,以  的概率向左或向右滚下,依次经过7次与小木块碰撞,最后掉入编号为1,2…,6的球槽内.例如小球要掉入3号球槽,则在前6次碰撞中有2次向右4次向左滚到第7层的第3个空隙处,再以
的概率向左或向右滚下,依次经过7次与小木块碰撞,最后掉入编号为1,2…,6的球槽内.例如小球要掉入3号球槽,则在前6次碰撞中有2次向右4次向左滚到第7层的第3个空隙处,再以  的概率向右滚下,或在前6次碰撞中有3次向右3次向左滚到第7层的第4个空隙处,再以
的概率向右滚下,或在前6次碰撞中有3次向右3次向左滚到第7层的第4个空隙处,再以  的概率向左滚下.
的概率向左滚下.
-
(1) 若进行一次高尔顿板试验,求小球落入第7层第6个空隙处的概率;
-
(2) 小明同学在研究了高尔顿板后,利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动,8元可以玩一次高尔顿板游戏,小球掉入
 号球槽得到的奖金为
号球槽得到的奖金为  元,其中
元,其中  .
. ①求
 的分布列:
的分布列:②高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小明同学能盈利吗?
 的左、右焦点,A是椭圆上一动点,圆C与F1A的延长线、F1F2的延长线以及线段AF2相切,若M(t,0)为一个切点,则( )
的左、右焦点,A是椭圆上一动点,圆C与F1A的延长线、F1F2的延长线以及线段AF2相切,若M(t,0)为一个切点,则( )
 和矩形
和矩形 所在平面互相垂直,
所在平面互相垂直, ,
,  ,
,  是线段
是线段 的中点.
的中点.
-
(1) 求证:
 平面
平面 ;
;
-
(2) 试在线段
 上确定一点
上确定一点 , 使
, 使 与
与 所成角是60°.
所成角是60°.
 , 则f(f(10))的值为 .
, 则f(f(10))的值为 .
|
付款方式 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
|
频数 |
35 |
25 |
| 10 | |
已知分3期付款的频率为 ![]() ,请以此100人作为样本,以此来估计消费人群总体,并解决以下问题:
,请以此100人作为样本,以此来估计消费人群总体,并解决以下问题:
(Ⅰ)从消费人群总体中随机抽选3人,求“这3人中(每人仅购买一部手机)恰好有1人分4期付款”的概率;
(Ⅱ)若销售一部苹果6S手机,顾客分1期付款(即全款),其利润为1000元;分2期或3期付款,其利润为1500元;分4期或5期付款,其利润为2000元。用X表示销售一部苹果6S手机的利润,求X的分布列及数学期望.

 时有害垃圾错误分类的重量加速增长
B . 当
时有害垃圾错误分类的重量加速增长
B . 当  时有害垃圾错误分类的重量匀速增长
C . 当
时有害垃圾错误分类的重量匀速增长
C . 当  时有害垃圾错误分类的重量相对于当
时有害垃圾错误分类的重量相对于当  时增长了30%
D . 当
时增长了30%
D . 当  时有害垃圾错误分类的重量相对于当
时有害垃圾错误分类的重量相对于当  时减少了1.8吨
时减少了1.8吨

 B .
B .  C .
C .  D .
D . 
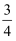 ,此椭圆的标准方程为( )
,此椭圆的标准方程为( )
 B .
B .  或
或  C .
C .  D .
D .  或
或 
.已知![]() 的值为 ( )
的值为 ( )
A.-2 B.2 C.![]() D.-
D.-![]()
已知f(x)是定义在[﹣1,1]上的增函数,且f(x﹣1)<f(1﹣3x),则x的取值范围是( )
A. B. C. D.
.设等差数列![]() 的前n项和为
的前n项和为![]() ,并且存在一个大于2的自然数k,使
,并且存在一个大于2的自然数k,使![]() 则( )
则( )
A.![]() 递增,
递增,![]() 有最小值 B.
有最小值 B.![]() 递增,
递增,![]() 有最大值
有最大值
C.![]() 递减,
递减,![]() 有最小值 D.
有最小值 D.![]() 递减,
递减,![]() 有最大值
有最大值
关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 是奇函数 B. 在区间![]() 上单调递增
上单调递增
C. ![]() 为其图象的一个对称中心 D. 最小正周期为
为其图象的一个对称中心 D. 最小正周期为![]()
- 下列条约中,使清政府完全变成“洋人的朝廷”的是 A.《南京条约》 B.《北京条约》 C.《马关条约》
- 在果实的发育过程中,子房壁发育成,子房中的胚珠发育成,胚珠里面的受精卵发育成,最终雌蕊的子房发育成.
- 徐州汉邦公司开辟了一条新疆旅游线路,丝绸之路是这条线路的主要旅游内容,导游在向游客介绍丝绸之路时,通常最先说起的中国朝代
- Expanding populations and steadily improving communicationsb
- 能正确表示我国长江流域梅雨天气成因的是:( ) A.副极地低压 B.反气旋 C.气旋 D.准静
- 如图所示,细线的一端系一质量为m的小球,另一端固定在倾角为θ的光滑斜面体顶端,细线与斜面平行,在斜面体以加速度a水平向右
- 1832年议会改革使英国的选民数从48.8万增加到80.8万,从人口总数的大约2%增加到3.3%。这些新获得选举权的人大
- -11的绝对值是A.11B.-11C.D.-
- 下图表示一种中枢神经元的联系方式,若在图中箭头处施一强刺激,则图中a、b、c、d、e能检测到兴奋的有几处…()A.2处
- 已知f(x)、g(x)都是定义域内的非奇非偶函数,而f(x)·g(x)是偶函数,写出满足条件的一组函数为:f(x)=__
- 已知0.1mol·L-1的二元酸H2A溶液的pH=4.0,则下列说法正确的是() A.在Na2A、NaHA两溶液中,离子
- 下列图形中,是正方体表面展开图的是() A. B C. D.
- 右面的乡村民居多出现在我国的_区,反映了该地区降水_ ( ) A.青藏地区,降水
- )如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.
- 仿照下面的画线句子,续写两句话,组成语意连贯的一段话。 现如今,个性早已成为新新人类的代名词。“你真有个性”成为一种语言
- 关于曲线运动,下列说法中正确的是:A、 在曲线运动中,质点速度的方向时刻改变,质点在某一点的速度方向是曲线在这一点的切线
- 美国“冷战”政策最基本的特征是
- “除犯有罪行等待交付罚款者外,不得拘留任何人或施以镣铐枷锁,债务人应以物品而不以人身作为借款之抵押品。”根据所学知识判
- 如图所示,斜面体B静置于水平桌面上,一质量为的木块A从斜面底端开始以初速度沿斜面上滑,然后又返回出发点,此时速度为,且。
- 一个物体由多个完全相同的小正方体组成,的三视图如图所示,那么组成这个物体的小正方体的个数为




