高中 数学
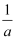 )<0的解是( )
)<0的解是( )
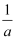 B .
B . 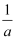 <x<a
C . x>
<x<a
C . x> 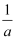 或x<a
D . x<
或x<a
D . x< 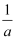 或x>a
或x>a
 (t是参数)和
(t是参数)和  (φ为参数).以原点O为极点,x轴的正半轴为极轴建立坐标系.
(φ为参数).以原点O为极点,x轴的正半轴为极轴建立坐标系.(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;
(Ⅱ)射线OM:θ=α(α∈[  ,
,  ])与曲线C1的交点为O,P,与曲线C2的交点为O,Q,求|OP|•|OQ|的最大值.
])与曲线C1的交点为O,P,与曲线C2的交点为O,Q,求|OP|•|OQ|的最大值.
①  ;
;
②  ;
;
③  ﹣
﹣ 
④ 
其结果是为零向量的个数是( )
 ,
,  ,则
,则  ( )
( )
 B .
B .  C .
C .  D .
D . 
 若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是.
若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是.
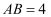 ,点D为线段AO的中点,点C为圆O上的一点,且
,点D为线段AO的中点,点C为圆O上的一点,且  ,
,  平面ABC,
平面ABC,  .
. 
-
(1) 求证:
 平面PAB.
平面PAB.
-
(2) 求二面角
 的余弦值.
的余弦值.
 ,满足
,满足 
-
(1) 求证:
 是奇函数;
是奇函数;
-
(2) 如果
 ,并且
,并且  ,试求
,试求  在区间
在区间  的最值.
的最值.
 三个入口,每个入口需要分配不少于2个且不多于3个志愿者,每名志愿者都要被分配,则3名女志愿者被分在同一个入口的概率为,每个入口都有女志愿者的分配方案共有种.
三个入口,每个入口需要分配不少于2个且不多于3个志愿者,每名志愿者都要被分配,则3名女志愿者被分在同一个入口的概率为,每个入口都有女志愿者的分配方案共有种.
 , 若方程f(x)+x=0有且仅有两个解,则实数a的取值范围是
, 若方程f(x)+x=0有且仅有两个解,则实数a的取值范围是
 与
与  夹角的大小为.
夹角的大小为.
 中,
中, 、
、 分别为棱
分别为棱 、
、 的中点,则直线
的中点,则直线 与平面
与平面 所成角的余弦值为( )
所成角的余弦值为( )
 B .
B .  C .
C .  D .
D . 
已知点![]() 表示
表示![]() 除以
除以![]() 余
余![]() ,
,
例如![]() ,
,![]() ,则如图所示的程序框图
,则如图所示的程序框图
的功能是( )
A. 求被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的最小正整数
的最小正整数
B. 求被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的最小正整数
的最小正整数
C. 求被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的最小正奇数
的最小正奇数
D. 求被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的最小正奇数
的最小正奇数

\
若两个平面α,β的法向量分别是n=(1,0,1),ν=(-1,1,0).则这两个平面所成的锐二面角的度数是________.
已知函数![]()
![]() ,在同一周期内, 当
,在同一周期内, 当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;当
;当![]()
![]() 时,
时,![]() 取得最
取得最![]() 小值
小值![]() .
.
(Ⅰ)求函数![]() 的解析式
的解析式![]() ;
;
(Ⅱ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅲ)若![]() 时,函数
时,函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
已知![]() 的三个内角A,B,C所对的三边分别是a,b,c,平面向量
的三个内角A,B,C所对的三边分别是a,b,c,平面向量![]() ,平面向量
,平面向量![]()
(1)如果![]() ,且
,且![]() 的面积
的面积![]() ,求a的值;
,求a的值;
(2)若![]() ,请判断
,请判断![]() 的形状.
的形状.
已知![]() 为实数,若复数
为实数,若复数![]() 为纯虚数,则
为纯虚数,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
某班级要从5名男生和2名女生中选出3人参加公益活动,则在选出的3人中男、女生均有的概率为 (结果用最简分数表示)
已知等差数列![]() 满足
满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,设正项等比数列
,设正项等比数列![]() 满足
满足![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和.
项和.
已知一个面积为24的正方体,内有一个与每条棱都相切的球,则此球的体积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知![]() (
(![]() )的图像关于坐标原点对称。
)的图像关于坐标原点对称。
(1)求![]() 的值,并求出函数
的值,并求出函数![]() 的零点;
的零点;
(2)若函数![]() 在
在![]() 内存在零点,求实数
内存在零点,求实数![]() 的取值范围;
的取值范围;
- 英国科学家达尔文的墓志铭是:“他把世界翻了一个个,虽然并不完全。”其中,“他把世界翻了—个个”是指达尔文( )A.发
- 1943年的德黑兰会议上,英国首相丘吉尔曾说:“我的一边坐着把一条腿搭在另一条腿上的巨大的俄国熊,另一边是巨大的北美野牛
- 生物世界广泛存在着变异,人们研究并利用变异可以培育高产、优质的作物新品种。下列能产生新基因的育种方式是 () A.“杂交
- 随着生活水平的提高与新产品的推广,电脑等废旧产品也加入了城市垃圾的行列。这主要反映了城市垃圾的什么特点?
- 广西是太平天国运动的发祥地之一,当地流传着这样的歌谣:“不怕清妖兵马足,天军引他到山麓,好比红薯堆进灶,大大小小一窝熟”
- 为除去下列物质中所含的少量杂质,括号中为杂质,写出所用试剂和反应的离子方程式: (1)FeSO4[Fe2(SO4)3]试
- 为推动社会主义文化的繁荣与发展,我国高度重视文化典籍的整理工作。这是基于 ①文化典籍是中华文化一脉相传的重要见证 ②优秀
- 电流做功的过程是将电能转化 能的过程.电流通过电动机做功,电能转化为 能;电流通过电热器做功,电能转化为
- (本小题满分12分) 在一次篮球练习课中,规定每人最多投篮5次,若投中2次就称为“通过”,若投中3次就称为“优秀”并停止
- 如图,在△ABC中,D是AB的中点,DE∥BC,若△ADE的面积为3,则△ABC的面积为()A.3 B.6
- 科学饮食是健康的保证,下列说法正确的是() ⑴维生素和无机盐都是人体必须的营养素 ⑵豆腐是富含蛋白质的食品 ⑶锌、硒等元
- 中草药秦皮中含有的七叶树内酯结构是,具有抗菌作用。若各取1 mol分别与浓溴水和NaOH溶液完全反应,则消耗Br2和Na
- 什么是力量?地震可以摧毁我们温馨的家园,摧毁我们美丽的山川,摧毁我们脆弱的生命,却摧毁不了我们自强的脊梁、空前的凝聚、缔
- 在某温度下反应ClF(气)+F2(气) ClF3(气)+268千焦在密闭容器中达到平衡.下列说法正确的是() A.温度不
- 下列叙述错误的是A.组成金属的粒子是原子B.金属晶体内部都有自由电子C.金属晶体内自由电子分布不均匀,专属于某个特定的金
- 下列动物不属于鱼类的是( )。 A、鲸鱼 B、鲨鱼 C、带鱼 D、
- 有一不纯的铁5.60g与足量的稀硫酸反应,放出0.21g氢气,则铁片中可能含有一种金属杂质为() A.Mg B.Zn
- 戊戌变法的失败表明 ①资产阶级改良道路在中国行不通 ②中国近代化的道路是漫长而坎坷的 ③封建顽固势力比较强大 ④资产阶级
- 下列词语没有错别字的一项是( ) A.执著追求 风餐露宿 开国元勋 为富不人 B.崭露头角 消声匿迹 节衣宿食 支掌门户
- 如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 .(任意添加一个符合题意的条件即可)



