高中 数学
已知实数  且
且  ,则在同一直角坐标系中,函数
,则在同一直角坐标系中,函数  的图象可能是( )
的图象可能是( )
 且
且  ,则在同一直角坐标系中,函数
,则在同一直角坐标系中,函数  的图象可能是( )
的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数f(x)是R上的偶函数,且在[0,+∞)上单调递增,则下列各式成立的是( )
A . f(﹣2)>f(0)>f(1)
B . f(﹣2)>f(﹣1)>f(0)
C . f(1)>f(0)>f(﹣2)
D . f(1)>f(﹣2)>f(0)
设  为实数,命题甲:
为实数,命题甲:  ,命题乙:
,命题乙:  ,则甲是乙的( )
,则甲是乙的( )
 为实数,命题甲:
为实数,命题甲:  ,命题乙:
,命题乙:  ,则甲是乙的( )
,则甲是乙的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
下列图象中,可以表示函数  的图象的是( )
的图象的是( )
 的图象的是( )
的图象的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的( )
A .  B .
B .  C .
C . 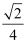 D .
D . 
 B .
B .  C .
C . 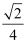 D .
D . 
已知点  ,点
,点  的坐标满足约束条件
的坐标满足约束条件  ,则
,则  的最小值为( )
的最小值为( )
 ,点
,点  的坐标满足约束条件
的坐标满足约束条件  ,则
,则  的最小值为( )
的最小值为( )
A .  B .
B .  C . 1
D .
C . 1
D . 
 B .
B .  C . 1
D .
C . 1
D . 
正方体ABCD﹣A'B'C'D'的棱长为a,连接A'C',A'D,A'B,BD,BC',C'D,得到一个三棱锥A'﹣BC'D.求:

-
(1) 求异面直线A'D与C'D′所成的角;
-
(2) 三棱锥A'﹣BC'D的体积.
对于两个变量的回归分析,下列说法正确的是( )
A . 两个随机变量线性相关性越强,相关系数 越接近1
B . 若由样本数据得到回归直线
越接近1
B . 若由样本数据得到回归直线 , 则其必过点
, 则其必过点 C . 线性回归方程
C . 线性回归方程 , 则当样本数据中
, 则当样本数据中 时,必有相应样本数据
时,必有相应样本数据 D . 残差平方和越小的模型,拟合的效果越好
D . 残差平方和越小的模型,拟合的效果越好
 越接近1
B . 若由样本数据得到回归直线
越接近1
B . 若由样本数据得到回归直线 , 则其必过点
, 则其必过点 C . 线性回归方程
C . 线性回归方程 , 则当样本数据中
, 则当样本数据中 时,必有相应样本数据
时,必有相应样本数据 D . 残差平方和越小的模型,拟合的效果越好
D . 残差平方和越小的模型,拟合的效果越好
已知菱形 的边长为2,
的边长为2, , 则
, 则 的值为( )
的值为( )
 的边长为2,
的边长为2, , 则
, 则 的值为( )
的值为( )
A . 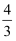 B .
B .  C .
C .  D .
D . 
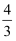 B .
B .  C .
C .  D .
D . 
银行定期储蓄存单的密码由6个数字组成,每个数字均是0~9中的一个,小王去银行取一笔到期的存款时,忘记了密码中某一位上的数字,他决定不重复地随机进行尝试,则不超过2次就按对密码的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,若
,若  ,则
,则  的值是( )
的值是( )
 ,若
,若  ,则
,则  的值是( )
的值是( )
A .  B .
B .  或
或  C .
C .  D .
D .  或
或 
 B .
B .  或
或  C .
C .  D .
D .  或
或 
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位建立坐标系,已知直线l的极坐标方程为2ρcosθ+ρsinθ=3,曲线C的参数方程为  (α为参数).
(α为参数).
 (α为参数).
(α为参数).
-
(1) 求曲线C的普通方程和直线l的直角坐标方程;
-
(2) P(1,1),设直线l与曲线C相交于A、B两点,求|PA|•|PB|的值.
如图给出的是计算  的值的一个程序框图,其中判断框内应填入的条件是( ).
的值的一个程序框图,其中判断框内应填入的条件是( ).
 的值的一个程序框图,其中判断框内应填入的条件是( ).
的值的一个程序框图,其中判断框内应填入的条件是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
执行下列程序后,输出的i的值是( )

A . 5
B . 6
C . 10
D . 11
函数  的图象可以由函数
的图象可以由函数  的图象经过( )
的图象经过( )
 的图象可以由函数
的图象可以由函数  的图象经过( )
的图象经过( )
A . 向右平移  个单位长度得到
B . 向右平移
个单位长度得到
B . 向右平移  个单位长度得到
C . 向左平移
个单位长度得到
C . 向左平移  个单位长度得到
D . 向左平移
个单位长度得到
D . 向左平移  个单位长度得到
个单位长度得到
 个单位长度得到
B . 向右平移
个单位长度得到
B . 向右平移  个单位长度得到
C . 向左平移
个单位长度得到
C . 向左平移  个单位长度得到
D . 向左平移
个单位长度得到
D . 向左平移  个单位长度得到
个单位长度得到
如图,PA与圆O相切于点A,PCB为圆O的割线,并且不过圆心,已知∠BPA=30°,PA=2![]() ,PC=1,则圆O的半径等于________.
,PC=1,则圆O的半径等于________.

如图,在斜三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求证:
,求证:![]() .
.
计算![]() ;
;
如图,已知平行四边形ABCD,点![]() 和
和![]() 分别将线段BC和DC
分别将线段BC和DC![]() 等分
等分![]() ,
,
若![]() ,则
,则![]()
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()

如图所示,定义域为![]() 上的函数
上的函数![]() 是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.
是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.

(1)求![]() 的解析式;
的解析式;
(2)若![]() 关于的方程
关于的方程![]() 有三个不同解,求
有三个不同解,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的取值集合.
的取值集合.
最近更新
- 我国饮用矿泉水的基本类别是碳酸水、硅酸水和锶水。此外还有锌、锂、溴、碘及硒矿泉水等,这里的锌、锂、溴、碘、硒是指 A
- “水的煮沸”和“水的分解”有什么本质区别?( ) A.前者发生化学变化,后者发生物理变化 B.前者得到纯净物,后
- 在探究串联电路中电压规律的实验中,小红同学将电阻R1、R2串联后接到电源上,如图(a)所示 ① 小红依照图
- 甲、乙两车从同一地点同向行驶,但是甲车做匀速直线运动,其速度为=20米/秒,乙车在甲车行驶至距离出发地125米处时开始以
- 下列大肠杆菌某基因的碱基序列的变化,对其所控制合成的多肽的氨基酸序列影响最大的是(不考虑终止密码子)A.第6位的C被替换
- 读“我国部分省区某年人口出生率、人口自然增长率和人口总数的统计图”,回答1~2题。 1.下列判断正确的是( ) A、
- 中国外汇交易中心公布,2013年1月31日,银行间外汇市场人民币汇率中间价为1美元对人民币6.2795元;2013年9月
- 下列图形中,既是轴对称图形又是中心对称图形的是A B C D
- 近亲结婚会增加后代遗传病的发病率,主要原因在于( ) A.近亲结婚容易使后代产生新的致病基因 B.近亲结婚的双方携带
- 用容量瓶配制一定物质的量浓度的溶液,该容量瓶必须是( ) A.干燥的 B.瓶塞不漏水的 C.用欲配制的溶
- 一质量为m的质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的。今把质点从O点
- 2015年5月,浙江网商银行获批开业,至此首批5家试点民营银行已全部获批开业。民营银行属于私营经济。下列对于私营经济认识
- 已知函数f(x)=x2-(a-1)x+5在区间上为增函数,那么f(2)的取值范围是________.
- 下列实例中,目的是为了减小摩擦的是() A.足球守门员戴有防滑手套 B.骑自行车的人刹车时用力捏闸 C.给自行车轴承中加
- 8.向下列溶液中通入过量CO2,最终出现浑浊的是()A.氢氧化钙饱和溶液
- 下列有关细胞的叙述中,不正确的一项是 A.植物体内,分生组织的细胞能分化形成其他组织 B.草履虫体内,物质的运输依靠的是
- Not until _______ 18 years old _______ a right to vote. A
- 下列叙述正确的是( ) A.2 mol NaOH的摩尔质量为80g/mol B.NH4+的摩尔质量为17 g/mo
- 第二节书面表达(满分25分) 自行车是公认的绿色交通工具,也是我过最普通的交通工具。但随着中国汽车拥有量的不断增加,自行
- 设直线kx-y+1=0被圆O:所截弦的中点的轨迹为C,则曲线C与直线x+y-1=0的位置关系为: A.相离



