高中 数学
给定四个函数:①  ;②
;②  ;③
;③  ;④
;④  .其中是奇函数的有.(填序号)
.其中是奇函数的有.(填序号)
 ;②
;②  ;③
;③  ;④
;④  .其中是奇函数的有.(填序号)
.其中是奇函数的有.(填序号)
- 已知
 ,若存在实数
,若存在实数 ,使函数
,使函数 有两个零点,则
有两个零点,则 的取值范围是 。
的取值范围是 。
设全集  ,集合
,集合  ,
,  ,则
,则  的值是( )
的值是( )
 ,集合
,集合  ,
,  ,则
,则  的值是( )
的值是( )
A . 2
B . -2
C . 8
D . -8
函数f(x)=3sin(πx)﹣  ,x∈[﹣3,5]的所有零点之和为.
,x∈[﹣3,5]的所有零点之和为.
 ,x∈[﹣3,5]的所有零点之和为.
,x∈[﹣3,5]的所有零点之和为.
已知函数  ,若对任意
,若对任意  ,总存在
,总存在  ,使得
,使得  ,则
,则  的取值范围是( )
的取值范围是( )
 ,若对任意
,若对任意  ,总存在
,总存在  ,使得
,使得  ,则
,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
我们知道,任何一个正整数N可以表示成N=a×10n(1≤a<10,n∈Z),此时lgN=n+lga(0≤lga<1).当n≥0时,N是一个n+1位数.已知lg5≈0.69897,则5100是( )位数.
A . 71
B . 70
C . 69
D . 68
已知α﹣β=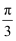 , cosα+cosβ=
, cosα+cosβ=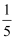 , 则cos
, 则cos =
=
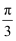 , cosα+cosβ=
, cosα+cosβ=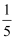 , 则cos
, 则cos =
=
若存在实数a,b,对任意实数x∈[0,4],使不等式  ﹣m≤ax+b≤
﹣m≤ax+b≤  +m恒成立,则m的取值范围为( )
+m恒成立,则m的取值范围为( )
 ﹣m≤ax+b≤
﹣m≤ax+b≤  +m恒成立,则m的取值范围为( )
+m恒成立,则m的取值范围为( )
A . m≥1
B . m≤1
C . m≤  D . m≥
D . m≥ 
 D . m≥
D . m≥ 
已知经过椭圆  的右焦点
的右焦点  的直线交椭圆于A,B两点,
的直线交椭圆于A,B两点,  是椭圆的左焦点,则
是椭圆的左焦点,则  的周长为( )
的周长为( )
 的右焦点
的右焦点  的直线交椭圆于A,B两点,
的直线交椭圆于A,B两点,  是椭圆的左焦点,则
是椭圆的左焦点,则  的周长为( )
的周长为( )
A . 10
B . 20
C . 30
D . 40
直线y=k(x-2)+4与曲线y=1+ 有两个不同的交点,则实数k的取值范围是( )
有两个不同的交点,则实数k的取值范围是( )
 有两个不同的交点,则实数k的取值范围是( )
有两个不同的交点,则实数k的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到下表数据:
|
单价 | | | | | |
| 销量 | | | | | |
且  ,
,  ,
,
-
(1) 已知
 与
与  具有线性相关关系,求出
具有线性相关关系,求出  关于
关于  回归直线方程;
回归直线方程;
-
(2) 解释回归直线方程中
 的含义并预测当单价为12元时其销量为多少?
的含义并预测当单价为12元时其销量为多少?
已知  且
且  则向量
则向量  在
在  方向上的投影为( )
方向上的投影为( )
 且
且  则向量
则向量  在
在  方向上的投影为( )
方向上的投影为( )
A .  B .
B .  C .
C .  D .
D . 
用秦九韶算法求函数 , 当
, 当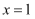 时的值时,
时的值时, .
.
 , 当
, 当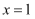 时的值时,
时的值时, .
.
直线  与曲线
与曲线  相切也与曲线
相切也与曲线  相切,则称直线
相切,则称直线  为曲线
为曲线  和曲线
和曲线  的公切线,已知
的公切线,已知  ,
,  ,直线
,直线  是
是  与
与  的公切线,则直线
的公切线,则直线  的方程为( )
的方程为( )
 与曲线
与曲线  相切也与曲线
相切也与曲线  相切,则称直线
相切,则称直线  为曲线
为曲线  和曲线
和曲线  的公切线,已知
的公切线,已知  ,
,  ,直线
,直线  是
是  与
与  的公切线,则直线
的公切线,则直线  的方程为( )
的方程为( )
A .  或
或 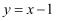 B .
B .  或
或  C .
C .  或
或  D .
D .  或
或 
 或
或 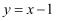 B .
B .  或
或  C .
C .  或
或  D .
D .  或
或 
函数 的部分图象大致为( )
的部分图象大致为( )
 的部分图象大致为( )
的部分图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元,求:
-
(1) 仓库顶部面积S的最大允许值是多少?
-
(2) 为使S达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
已知函数 . 若存在实数k使得函数f(x)的值域为[﹣1,1],则实数a的取值范围是( )
. 若存在实数k使得函数f(x)的值域为[﹣1,1],则实数a的取值范围是( )
 . 若存在实数k使得函数f(x)的值域为[﹣1,1],则实数a的取值范围是( )
. 若存在实数k使得函数f(x)的值域为[﹣1,1],则实数a的取值范围是( )
A . [ ,
,  ]
B . [2,
]
B . [2, ]
C . [1,3]
D . [2,3]
]
C . [1,3]
D . [2,3]
 ,
,  ]
B . [2,
]
B . [2, ]
C . [1,3]
D . [2,3]
]
C . [1,3]
D . [2,3]
图中阴影部分表示的集合是( )

A . ∁U(A∩B)
B . A∩(∁UB)
C . B∩(∁UA)
D . ∁U(A∪B)
在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共
A.56个 B.57个 C.58个 D.60个
如图,某校有一块形如直角三角形![]() 的空地,其中
的空地,其中![]() 为直角,
为直角,![]() 长
长![]() 米,
米, ![]() 长
长![]() 米,现欲在此空地上建造一间健身房,其占地形状为矩形,且
米,现欲在此空地上建造一间健身房,其占地形状为矩形,且![]() 为矩形的一个顶点,求该健身房的最大占地面积.
为矩形的一个顶点,求该健身房的最大占地面积.


最近更新
- 下列仪器使用时不允许用酒精灯加热的是() A. 量筒 B.
- 下列有关能量的判断或表示方法正确的是 A.从C(石墨)=C(金刚石) ΔH=1.9 kJ·mol-1,可知金刚石比石墨
- 关于“北京时间”错误的是( ) A.北京的地方时 B.东八区的区时 C.我国采用的标准时间 D.东经120°
- 下面是对日常生活中一些物体的质量和长度的估测,其中最接近实际的是:( )A.一袋方便面的质量约为500gB.一位中学
- 设,若,则( ) A. B. C. D.
- 第二节 完形填空(共20小题,每小题1.5分,满分30分) 阅读下面短文,掌握其大意,然后从36—55各题所给的A、B、
- 读下图,回答(1)图中所示的三大综合工业中心是 A.武汉、鄂州、黄石 B.武汉、麻城、黄石 C.武穴、鄂州、黄石
- 15.在下面一段文字的横线处补写恰当的语句,使整段文字语意完整连贯,内容贴切,逻辑严密。每处不超过15个字。(6分) 《
- 《中国大百科全书》中写道:“中国古代社会中凭借血缘关系对族人进行管辖和处置的制度与中国古代社会中的宗族组织相配合,是统治
- 32.关于植物激素作用的叙述,正确的是( ) A.生长素可用于果实催熟 B.脱落酸能够促进种子萌发 C.赤霉素能
- 阅读下面的文字,完成5~7题。上世纪六十年代,在山东出土了一件龙山文化时期的空足白陶。它的基本器型特点是,有一个从颈部向
- 如图为神经递质合成酶基因复制、表达的有关过程。下列相关分析中错误的是 ()。A.①过程需要模板、原料、酶和能
- 如图,在△ABC中,∠B=90°,AB=6㎝,BC=8㎝。点P从A开始沿AB边向点B以1㎝∕s的速度移动,点Q从点B开始
- 在如下图所示的电路图中,“开关A的闭合”是“灯泡B亮”的 条件.( ) A.充分不必要B.必要不充分C
- 关于化学反应速率、化学平衡的说法中错误的是( ) A.其它条件不变时,升高温度化学反应速率加快 B.
- 我国是社会主义国家,必须坚持马克思主义的指导地位,坚持马克思主义又是与发展马克思主义相统一的,不发展马克思主义就谈不上坚
- PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大。2012年
- 下列各组物质的晶体中,化学键类型相同、晶体类型也相同的是:() A.SO2和SiO2 B.CCl4和KCl
- 下图为我国部分地区某时刻的地面天气形势图。读图回答29~30题。29.甲、乙、丙、丁四地中风速最大的是 () A.甲
- (本小题满分12分)已知椭圆方程为,它的一个顶点为,离心率.(1)求椭圆的方程;(2)设直线与椭圆交于A,B两点,坐标