高中 数学
设点P到点(﹣1,0)、(1,0)距离之差为2m,到x、y轴的距离之比为2,求m的取值范围
已知椭圆C1和双曲线C2焦点相同,且离心率互为倒数,F1 , F2它们的公共焦点,P是椭圆和双曲线在第一象限的交点,当∠F1PF2=60°时,则椭圆C1的离心率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在  中,内角
中,内角 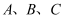 的对边分别为
的对边分别为 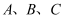 ,且
,且  .
.
 中,内角
中,内角 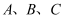 的对边分别为
的对边分别为 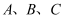 ,且
,且  .
. (Ⅰ)求角  的大小;
的大小;
(Ⅱ)若  ,
,  的面积为
的面积为  ,求
,求  的值.
的值.
命题“∃x∈R,ex>x”的否定是 .
若不等式x2﹣ax+b<0的解集为(1,2),则不等式  <
<  的解集为( )
的解集为( )
 <
<  的解集为( )
的解集为( )
A . ( 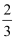 ,+∞)
B . (﹣∞,0)∪(
,+∞)
B . (﹣∞,0)∪(  ,+∞)
C . (
,+∞)
C . (  ,+∞)
D . (﹣∞,0)∪(
,+∞)
D . (﹣∞,0)∪( 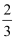 ,+∞)
,+∞)
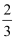 ,+∞)
B . (﹣∞,0)∪(
,+∞)
B . (﹣∞,0)∪(  ,+∞)
C . (
,+∞)
C . (  ,+∞)
D . (﹣∞,0)∪(
,+∞)
D . (﹣∞,0)∪( 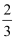 ,+∞)
,+∞)
若点P(sinα,tanα)在第三象限,则角α是( )
A . 第一象限角
B . 第二象限角
C . 第三象限角
D . 第四象限角
已知函数  ,
,  .
.
 ,
,  .
.
-
(1) 讨论函数
 的单调性;
的单调性;
-
(2) 若
 对
对  恒成立,求实数
恒成立,求实数  的取值范围.
的取值范围.
设x,y满足约束条件 , 若目标函数z=ax+by(a>0, b>0)的最大值为8,点P为曲线
, 若目标函数z=ax+by(a>0, b>0)的最大值为8,点P为曲线 上动点,则点P到点(a,b)的最小距离为( )
上动点,则点P到点(a,b)的最小距离为( )
 , 若目标函数z=ax+by(a>0, b>0)的最大值为8,点P为曲线
, 若目标函数z=ax+by(a>0, b>0)的最大值为8,点P为曲线 上动点,则点P到点(a,b)的最小距离为( )
上动点,则点P到点(a,b)的最小距离为( )
A .  B . 0
C .
B . 0
C .  D . 1
D . 1
 B . 0
C .
B . 0
C .  D . 1
D . 1
已知非空集合S={x|﹣ ≤x≤m}满足:当k∈S时,有x2∈S,则实数m的取值范围是
≤x≤m}满足:当k∈S时,有x2∈S,则实数m的取值范围是
 ≤x≤m}满足:当k∈S时,有x2∈S,则实数m的取值范围是
≤x≤m}满足:当k∈S时,有x2∈S,则实数m的取值范围是
已知集合  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知

-
(1) 若
 , 求
, 求 的最小值;
的最小值;
-
(2) 当
 时,
时, , 求a的取值范围
, 求a的取值范围
过双曲线 的左焦点F作圆
的左焦点F作圆 的两条切线,切点分别为A、B,双曲线左顶点为M,若
的两条切线,切点分别为A、B,双曲线左顶点为M,若 , 则该双曲线的离心率为 ( )
, 则该双曲线的离心率为 ( )
 的左焦点F作圆
的左焦点F作圆 的两条切线,切点分别为A、B,双曲线左顶点为M,若
的两条切线,切点分别为A、B,双曲线左顶点为M,若 , 则该双曲线的离心率为 ( )
, 则该双曲线的离心率为 ( )
A .  B .
B .  C . 3
D . 2
C . 3
D . 2
 B .
B .  C . 3
D . 2
C . 3
D . 2
由与圆心距离相等的两条弦长相等,想到与球心距离相等的两个截面圆的面积相等,用的是( )
A . 三段论推理
B . 类比推理
C . 归纳推理
D . 传递性关系推理
向量 经矩阵
经矩阵 变化后得到的矩阵为 .
变化后得到的矩阵为 .
 经矩阵
经矩阵 变化后得到的矩阵为 .
变化后得到的矩阵为 .
设  ,将
,将  表示成指数幂的形式,其结果是( )
表示成指数幂的形式,其结果是( )
 ,将
,将  表示成指数幂的形式,其结果是( )
表示成指数幂的形式,其结果是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
复数![]() 满足
满足![]() ,则在复平面内复数
,则在复平面内复数![]() 所对应的点位于
所对应的点位于
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
根据统计,某机械零件加工厂的一名工人组装第![]() (
(![]() )件产品所用的时间(单
)件产品所用的时间(单![]() 位:分钟)为
位:分钟)为 (
(![]() 为常数).已知该工人组装第
为常数).已知该工人组装第![]() 件产品用时
件产品用时![]() 小时.
小时.
(1)求![]() 的值;
的值;
(2)试问该工人组装第![]() 件产品比组装第
件产品比组装第![]() 件产品少用多少时间?
件产品少用多少时间?
等腰三角形一腰上的高是![]() ,这条高与底边的夹角为
,这条高与底边的夹角为![]() ,则底边长=( )
,则底边长=( )
A.2 B.![]() C.3 D.
C.3 D.![]()
已知![]() (
(![]() 为虚数单位),则“
为虚数单位),则“![]() ”是“
”是“![]() 为纯虚数”的 ()
为纯虚数”的 ()
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )

A. 3,5 B. 5,5 C. 3,7 D. 5,7
最近更新
- 70.(2016·四川乐山二模·32)17世纪自然神论创始人赫尔伯特说:“神造了世界却不照管护理这个世界,任其发展”。认
- 下列各词中,没有语病的一句是( ) A.这位曾经驰骋乒坛的名将已经回到了祖国,现就任于北京大学医学部教授
- 因式分解:3x﹣12x3
- 图甲表示水稻的叶肉细胞在光照强度分别为a、b、c、d时,单位时间内CO2释放量和O2产生总量的变化。图乙表示蓝藻光合作用
- 在美国,无论是总统选举还是议会选举,民主党和共和党都要竭力为本党争取尽可能多的职位,这主要是因为 A. 他们热爱自己的党
- 班超投笔从戎,立功西域,被封为定远侯,他在西域的主要活动是( ) ①派甘英出使大秦 ②出使大宛、大月氏
- 下图漫画《精简前后》主要是告诫政府,在机构改革中必须()精简前后 A.把握住事物发展的方向,相信改革前景是光明的 B.树
- (NH4)2SO4在强热条件下发生分解,生成NH3、SO2、N2和H2O。该反应的生成物中氧化产物和还原产物的物质的量之
- 完形填空 Who did this? Mrs. Green asked with a piece of broken
- 阅读文言文,按要求回答问题(每题3分,共9分) 爱 莲 说 周敦颐 水陆草木之花,可爱者甚蕃。晋陶渊明独
- 《“十三五”规划建议》提出:实行脱贫工作责任制,强化脱贫工作责任考核,对贫困县重点考核脱贫成效,促进定点扶贫和精准扶贫。
- 如图所示,质量为m=50g,长l=10cm的铜棒,用长度相等的两根轻软导线悬吊在竖直向上的匀强磁场中,导线跟铜棒的接触良
- 溶质的质量分数为14%的KOH溶液,经加热蒸发去100 g水后,质量分数变成28%,体积为80 mL,则此时溶液的物质的
- 已知一直角三角形,两直角边的平方和是100cm2,则其斜边上的中线长为__________cm.
- 以农产品为主的生活必需品价格上涨,加重了城乡居民特别是中低收入群体的生活负担,引起了政府的高度重视。稳定物价,政府可以
- ---How do you study for a test?---________.A.For listening t
- 蛋白质分子能被肽酶降解,至于哪一个肽键被断裂则决定于肽酶的类型。肽酶P能断裂带有 侧链R4 的氨基酸和相邻氨基酸的羧基基
- 下列句中加点的成语,运用恰当的一项是( ) A.处处以保护人权自居的美国在南联盟投下的一枚枚炸弹,使他们的人权嘴脸
- 下图是质谱仪的工作原理示意图,带电粒子被加速电场加速后,进入速度选择器。速度选择器内互相垂直的匀强磁场和匀强电场的强度分
- 四支试管分别充满O2、NO2、Cl2、NH3四种气体,把它们分别倒立于盛有下列各种液体的水槽中,产生的现象如下图所示,其



