高中 数学
三角形ABC中,  ,
,  边上的高等于
边上的高等于  ,则
,则  ( )
( )
 ,
,  边上的高等于
边上的高等于  ,则
,则  ( )
( )
A .  B .
B .  C . 2
D . -2
C . 2
D . -2
 B .
B .  C . 2
D . -2
C . 2
D . -2
如图,在单位圆  中,
中,  为圆上的一个定点,
为圆上的一个定点,  为圆上的一个动点,
为圆上的一个动点,  的取值范围为.
的取值范围为.
 中,
中,  为圆上的一个定点,
为圆上的一个定点,  为圆上的一个动点,
为圆上的一个动点,  的取值范围为.
的取值范围为. 
在  的展开式中
的展开式中  的系数为( )
的系数为( )
 的展开式中
的展开式中  的系数为( )
的系数为( )
A . 168
B . 84
C . -42
D . -84
最小正周期为 的函数有( )
的函数有( )
 的函数有( )
的函数有( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知三棱锥S﹣ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为( )
A .  B .
B .  C .
C .  D .
D . 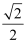
 B .
B .  C .
C .  D .
D . 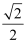
对于函数 (
( 且
且 ),
), , 在同一直角坐标系下的图象可能为( )
, 在同一直角坐标系下的图象可能为( )
 (
( 且
且 ),
), , 在同一直角坐标系下的图象可能为( )
, 在同一直角坐标系下的图象可能为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若复数z满足  其中i为虚数单位,则z=( )
其中i为虚数单位,则z=( )
 其中i为虚数单位,则z=( )
其中i为虚数单位,则z=( )
A . 1+2i
B . 1  2i
C .
2i
C .  D .
D . 
函数f(x)=sin(ωx+ 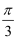 )(ω>0)的图象的相邻两条对称轴间的距离是
)(ω>0)的图象的相邻两条对称轴间的距离是  .若将函数f(x)的图象向右平移
.若将函数f(x)的图象向右平移  个单位,再把图象上每个点的横坐标缩小为原来的一半,得到g(x),则g(x)的解析式为( )
个单位,再把图象上每个点的横坐标缩小为原来的一半,得到g(x),则g(x)的解析式为( )
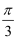 )(ω>0)的图象的相邻两条对称轴间的距离是
)(ω>0)的图象的相邻两条对称轴间的距离是  .若将函数f(x)的图象向右平移
.若将函数f(x)的图象向右平移  个单位,再把图象上每个点的横坐标缩小为原来的一半,得到g(x),则g(x)的解析式为( )
个单位,再把图象上每个点的横坐标缩小为原来的一半,得到g(x),则g(x)的解析式为( )
A . g(x)=sin(4x+  )
B . g(x)=sin(8x﹣
)
B . g(x)=sin(8x﹣ 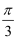 )
C . g(x)=sin(x+
)
C . g(x)=sin(x+  )
D . g(x)=sin4x
)
D . g(x)=sin4x
 )
B . g(x)=sin(8x﹣
)
B . g(x)=sin(8x﹣ 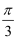 )
C . g(x)=sin(x+
)
C . g(x)=sin(x+  )
D . g(x)=sin4x
)
D . g(x)=sin4x
已知函数f(x)的定义域为[﹣1,2],则函数g(x)=f(2x﹣  )的定义域为( )
)的定义域为( )
 )的定义域为( )
)的定义域为( )
A . [  ,
,  ]
B . [1,
]
B . [1,  ]
C . [﹣1,
]
C . [﹣1,  ]
D . [﹣1,
]
D . [﹣1,  ]
]
 ,
,  ]
B . [1,
]
B . [1,  ]
C . [﹣1,
]
C . [﹣1,  ]
D . [﹣1,
]
D . [﹣1,  ]
]
设向量  =(cos25°,sin25°),
=(cos25°,sin25°),  =(cos25°,sin155°),则
=(cos25°,sin155°),则  的值为( )
的值为( )
 =(cos25°,sin25°),
=(cos25°,sin25°),  =(cos25°,sin155°),则
=(cos25°,sin155°),则  的值为( )
的值为( )
A .  B . 1
C .
B . 1
C .  D .
D . 
 B . 1
C .
B . 1
C .  D .
D . 
设向量  =(1,﹣3),
=(1,﹣3),  =(﹣2,4),
=(﹣2,4),  =(﹣1,﹣2),若表示向量4
=(﹣1,﹣2),若表示向量4  ,4
,4  ﹣2
﹣2  ,2(
,2(  ﹣
﹣  ),
),  的有向线段首尾相连能构成四边形,则向量
的有向线段首尾相连能构成四边形,则向量  为( )
为( )
 =(1,﹣3),
=(1,﹣3),  =(﹣2,4),
=(﹣2,4),  =(﹣1,﹣2),若表示向量4
=(﹣1,﹣2),若表示向量4  ,4
,4  ﹣2
﹣2  ,2(
,2(  ﹣
﹣  ),
),  的有向线段首尾相连能构成四边形,则向量
的有向线段首尾相连能构成四边形,则向量  为( )
为( )
A . (2,6)
B . (﹣2,6)
C . (2,﹣6)
D . (﹣2,﹣6)
已知命题p:x2+2x-3>0,命题q:  >1,若p∧(¬q)为真命题,则x的取值范围是.
>1,若p∧(¬q)为真命题,则x的取值范围是.
 >1,若p∧(¬q)为真命题,则x的取值范围是.
>1,若p∧(¬q)为真命题,则x的取值范围是.
已知集合  ,若
,若  ,则实数
,则实数  的取值范围是( )
的取值范围是( )
 ,若
,若  ,则实数
,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(﹣x)+x的解集为( )

A . {x|﹣ <x<0或
<x<0或 <x≤2}
B . {x|﹣2≤x<﹣
<x≤2}
B . {x|﹣2≤x<﹣ 或
或 <x≤2}
C . {x|﹣2≤x<﹣
<x≤2}
C . {x|﹣2≤x<﹣ 或
或 <x≤2}
D . {x|﹣
<x≤2}
D . {x|﹣ <x<
<x< , 且x≠0}
, 且x≠0}
 <x<0或
<x<0或 <x≤2}
B . {x|﹣2≤x<﹣
<x≤2}
B . {x|﹣2≤x<﹣ 或
或 <x≤2}
C . {x|﹣2≤x<﹣
<x≤2}
C . {x|﹣2≤x<﹣ 或
或 <x≤2}
D . {x|﹣
<x≤2}
D . {x|﹣ <x<
<x< , 且x≠0}
, 且x≠0}
已知集合 ,
,  , 则
, 则 ( )
( )
 ,
,  , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
(1-i)2·i等于( )
A . 2-2i
B . 2+2i
C . -2
D . 2
如图,四边形ABCD中,∠ABC=∠C=120°,AB=4,BC=CD=2,则该四边形的面积是.

已知集合![]() ,求实数m的取值范围.
,求实数m的取值范围.
某校1 000名学生的某次数学考试成绩X服从正态分布,其密度函数
![]() 曲线如图所示,正态变量X在区间
曲线如图所示,正态变量X在区间![]() ,
,![]() ,
,![]() 内取值的概率分别是
内取值的概率分别是![]() ,
,![]() ,
,![]() ,则成绩X位于区间(52,68]的人数大约是( )
,则成绩X位于区间(52,68]的人数大约是( )

A. 997
B. 954
C. 683
D. 341
已知数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}中bn>0(n∈N*),且b1+b2+b3=15,又a1+b1、a2+b2、a3+b3成等比数列.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)求数列{an•bn}的前n项和Tn.
最近更新
- Reading without stop is a ______ piece of work.A. tire B.
- 阅读下面选文,完成20—24题。(15分) 改变命运的一分 ①办公室只剩下秦老师一个人的时候,门被推开了一条缝,
- 2009年10月31日,中国航天科技事业的先驱和杰出代表,被誉为“中国航天之父”和“火箭之王”的科学巨星 在
- 结合下述材料,探讨有关问题。 材料一 2001年我国流动人口的有关数据(1)2001年我国跨省流动人口的主要流向是
- 《咏史》:郁郁涧底松,离离山上苗。以彼径寸茎,荫此百尺条。世胄蹑高位,英俊沉下僚。地势使之然,由来非一朝。材料反映了 A
- 廉洁文化是中华优秀传统文化的组成部分,是宝贵的道德教育资源。《楚辞》有“朕幼清以廉洁兮”之语,东汉王逸有“不受曰廉,不污
- 我国航天人发扬“特别能吃苦,特别能战斗,特别能攻关,特别能奉献”的航天精神,将中国人的飞天梦想变成了现实。这里的航天精神
- Asthe saying goes,“No news ________ good news.” A.are
- 下列针对绿色植物植株、花、果实和种子示意图的叙述,不正确的是()A.图甲植株根吸收的水分通过根、茎、叶中的导管运输到植株
- 指数函数在R上是增函数,则的取值范围是( )A. B. C. D.
- “物以类聚,人以群分”,所以,我们只能和那些表现好的同学交往。(1)判断:( )(2)理由:
- 将1cm3的油酸溶于酒精,制成200cm3的油酸酒精溶液,已知1cm3溶液有50滴,现将1滴溶液滴到水面上,随着酒精溶于
- 如图1,把边长为4的正三角形各边分成四等分,连结各分点得到16个小正三角形.1.如图2,连结小正三角形的顶点得到一个正六
- 在△ABC中,(a+b+c)(a+b-c)=3ab,2cosAsinB=sinC,试判断△ABC的形状.
- The former Olympic champion was ______ in the quarterfinals
- (1)计算:(2)已知:,求的值.
- (9分)环丙烷可作为全身麻醉剂,环己烷是重要的有机溶剂。下面是部分环烷烃及烷烃衍生物的结构简式、键线式和某些有机化合物的
- (辨析)村民自治的目标是村民自主管理村里的日常事务。
- 金属镍及其化合物能发生如下反应: ①Ni+2HClNiCl2+H2↑ ②NiO+2HClNiCl2+H2O
- “德意志民族曾经号称‘思想家和诗人的民族’,也涌现出了一流的科学家和艺术家。……但是,这个伟大的民族曾经在一个狂人的操纵



