高中 数学
 .
.
给出8个函数:①y=2x , ②y=(  )x , ③y=log2x,④y=log0.5x,⑤y=x2 , ⑥y=
)x , ③y=log2x,④y=log0.5x,⑤y=x2 , ⑥y=  ,⑦y=sinx,⑧y=tanx.下列说法正确的是( )
,⑦y=sinx,⑧y=tanx.下列说法正确的是( )
 )x , ③y=log2x,④y=log0.5x,⑤y=x2 , ⑥y=
)x , ③y=log2x,④y=log0.5x,⑤y=x2 , ⑥y=  ,⑦y=sinx,⑧y=tanx.下列说法正确的是( )
,⑦y=sinx,⑧y=tanx.下列说法正确的是( )
A . 定义域是R的函数共有6个
B . 偶函数只有1个
C . 图象都不经过第三象限的函数共有6个
D . 满足f(x+2π)=f(x)的函数只有2个
过两点  和
和  的直线在
的直线在  轴上的截距是.
轴上的截距是.
 和
和  的直线在
的直线在  轴上的截距是.
轴上的截距是.
在  中,内角A , B , C的对边分别为a , b , c , 若
中,内角A , B , C的对边分别为a , b , c , 若  ,
,  ,
,  ,则c的值等于( )
,则c的值等于( )
 中,内角A , B , C的对边分别为a , b , c , 若
中,内角A , B , C的对边分别为a , b , c , 若  ,
,  ,
,  ,则c的值等于( )
,则c的值等于( )
A .  B .
B . 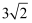 C .
C .  D .
D . 
 B .
B . 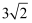 C .
C .  D .
D . 
已知椭圆的中心在原点,焦点在  轴上,离心率为
轴上,离心率为  ,且经过点
,且经过点  ,直线
,直线  交椭圆于不同的两点
交椭圆于不同的两点  ,
,  .
.
 轴上,离心率为
轴上,离心率为  ,且经过点
,且经过点  ,直线
,直线  交椭圆于不同的两点
交椭圆于不同的两点  ,
,  .
.
-
(1) 求椭圆的方程;
-
(2) 求
 的取值范围;
的取值范围;
-
(3) 若直线
 不过点
不过点  ,试问直线
,试问直线  ,
,  的斜率之和是否为定值,若是定值求出定值,若不是定值说明理由.
的斜率之和是否为定值,若是定值求出定值,若不是定值说明理由.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=π/2,AB=BC=2AD=4,E,F分别是AB,CD上的点,EF∥BC,AE=x,G是BC的中点,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
-
(1) 当x=2时,①求证:BD⊥EG;②求二面角D﹣BF﹣C的余弦值;
-
(2) 三棱锥D﹣FBC的体积是否可能等于几何体ABE﹣FDC体积的一半?并说明理由.
设数列{an}的前n项和为Sn , 对任意的正整数n,都有an=5Sn+1成立,bn=﹣1﹣log2|an|,数列{bn}的前n项和为Tn , cn=  .
.
 .
.
-
(1) 求数列{an}的通项公式与数列{cn}前n项和An;
-
(2) 对任意正整数m、k,是否存在数列{an}中的项an , 使得|Sm﹣Sk|≤32an成立?若存在,请求出正整数n的取值集合,若不存在,请说明理由.
小华、小明、小李小章去A,B,C三个工厂参加社会实践,要求每个工厂都有人去,且这四人都在这三个工厂实践,则小华和小李都没去B工厂的概率是.
数列  是等差数列,且
是等差数列,且  ,
,  ,那么
,那么  ( )
( )
 是等差数列,且
是等差数列,且  ,
,  ,那么
,那么  ( )
( )
A .  B .
B .  C . 5
D . -5
C . 5
D . -5
 B .
B .  C . 5
D . -5
C . 5
D . -5
已知函数 ,
,  , 如图所示,则图象对应的解析式可能是( ).
, 如图所示,则图象对应的解析式可能是( ).
 ,
,  , 如图所示,则图象对应的解析式可能是( ).
, 如图所示,则图象对应的解析式可能是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
cos45°sin15°﹣sin45°cos15°的值为.
已知函数  满足对任意的
满足对任意的  ,都有
,都有  恒成立,那么实数
恒成立,那么实数  的取值范围是
的取值范围是
 满足对任意的
满足对任意的  ,都有
,都有  恒成立,那么实数
恒成立,那么实数  的取值范围是
的取值范围是
气象意义上从春季进入夏季的标志为:“连续5天的日平均温度均不低于22 ℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
① 甲地:5个数据的中位数为24,众数为22;
② 乙地:5个数据的中位数为27,总体均值为24;
③ 丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区有 ( )
① 甲地:5个数据的中位数为24,众数为22;
② 乙地:5个数据的中位数为27,总体均值为24;
③ 丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区有 ( )
A . 3个
B . 2个
C . 1个
D . 0个
设全集为R,函数  的定义域为M,则
的定义域为M,则  =( )
=( )
 的定义域为M,则
的定义域为M,则  =( )
=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数f(x)= ﹣1的图象大致是( )
﹣1的图象大致是( )
 ﹣1的图象大致是( )
﹣1的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有种不同的排法.(用数字作答)
假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知 ,
, .
.
 ,
,![]()
(1)求![]() ,
,![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
,
设直线![]() 相交于A、B两个不同的点,与x轴相交于点F。
相交于A、B两个不同的点,与x轴相交于点F。
(1)证明:![]() ;
;
(2)若F是椭圆的一个焦点,且以AB为直径的圆过原点,求a2。
已知集合![]() ,则下列式子表示正确的有( )
,则下列式子表示正确的有( )
①![]() ②
②![]() ③
③![]() ④
④![]()
A.1个 B.2个 C.3个 D.4个
若函数f(x)=2|x﹣a|(a∈R)满足f(2+x)=f(2﹣x),且f(x)在[m,+∞)上单调递增,则实数m的最小值为 .
最近更新
- —Are those ______shoes ? — No,they’re not ______
- 根据下面材料,在你了解了人物的心事后,请你以同学的身份,写一句有分寸的宽慰、鼓励对方的短信。(4分) 晓敏时常表现得与
- What he regrets is that more than a chance .A.were
- 16.有一个学习小组在探究某种淀粉酶的最适温度时,设计了如下实验步骤: 1 取10支试管分成5组,编号,向每组的1支试管
- 关于城市化的错误叙述是 A.城市化过程是农村人口向城市集聚 B.城市化是社会经济发展的必然结果 C.城市化水平体现
- 下列关于力的说法中,正确的是( )A.只有直接接触的物体之间才可能有力的作用B.力可以脱离物体而单独存在C.只施力
- 函数的值域是( ) A. B. C. D.
- (二)文言文阅读(15分) 阅读下面的文言文,完成2—5题。 先生金姓,采名,若采字,吴县诸生也。为人倜傥
- Everyone had a form in his hand, but no one knew which offic
- 下列关于反射弧和兴奋传导的叙述,不正确的是() A.神经受刺激的部位膜外先变为正电位,接着又恢复负电位,形成电信号在神经
- 黄宗羲认为:“秦变封建而为郡县,以郡县得私于我也;汉建庶孽(指诸侯王国),以其可以藩屏于我也;宋解方镇之兵,以方镇之不利
- During the ten-day vacation, they traveled to France their o
- 石灰石是我省的主要矿产之一.学校研究性学习小组为了测定当地矿山石灰石中碳酸钙的质量分数,取来了一些矿石样品,并取稀盐酸2
- 下列是扬州瘦西湖风景区的几幅图片,关于图片的说法正确的是A.雾是液化现象,吸热B.霜是凝华现象,放热C.雪是凝华现象,吸
- 甲、乙、丙三辆赛车同时从起点出发,做匀速直线运动,最先到达终点的是丙车.甲、乙两车的路程和时间的s—t图像如图所示,下列
- 某芳香烃A有如下转化关系: 按要求填空:(1)写出反应②和⑤的反应条件:②___________________;⑤__
- 演示自感现象的实验电路如图所示,L是电感线圈,A1、A2是规格相同的灯泡,R的阻值与L的直流电阻值相同.当开关S由断开到
- 西周统治末期,所面临的矛盾有( ) ①阶级矛盾 ②民族盾 ③统治
- 云南某地梯田规模巨大,级数最多的达5000级,现已成为中外闻名的观光景点。当初修建梯田的主要目的是 A.保持水土
- Scientistsfrom the United States say they have found fish an



