高中 数学
已知函数f(x-1)=x2-3,则f(2)的值为( )
A . -2
B . 6
C . 1
D . 0
已知复数  的共轭复数
的共轭复数  ,且
,且  .
.
 的共轭复数
的共轭复数  ,且
,且  .
.
-
(1) 求
 的值;
的值;
-
(2) 若过点
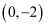 的直线
的直线  的斜率为
的斜率为  ,求直线
,求直线  与曲线
与曲线  以及
以及  轴所围成的图形的面积.
轴所围成的图形的面积.
已知圆  上存在两点
上存在两点  ,
,  关于直线
关于直线  对称,则
对称,则  的最小值是( )
的最小值是( )
 上存在两点
上存在两点  ,
,  关于直线
关于直线  对称,则
对称,则  的最小值是( )
的最小值是( )
A . 1
B . 8
C . 2
D . 4
设集合A={(x,y)| },则区域A的面积为
},则区域A的面积为
 },则区域A的面积为
},则区域A的面积为
设a,b,c∈R,对任意满足|x|≤1的实数x,都有|ax2+bx+c|≤1,则|a|+|b|+|c|的最大可能值为
若  ,则
,则  的取值范围是( )
的取值范围是( )
 ,则
,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,则
,则  的值为.
的值为.
 ,则
,则  的值为.
的值为.
已知函数 , 若
, 若 对
对 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
 , 若
, 若 对
对 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设函数  的最大值为M,最小正周期为T.
的最大值为M,最小正周期为T.
 的最大值为M,最小正周期为T.
的最大值为M,最小正周期为T. (Ⅰ)求M、T;
(Ⅱ)若有10个互不相等的正数xi满足f(xi)=M,且xi<10π(i=1,2,…,10),求x1+x2+…+x10的值.
在等比数列 中,
中, , 则
, 则 的公比q=.
的公比q=.
 中,
中, , 则
, 则 的公比q=.
的公比q=.
已知函数  则下列判断正确的有( )
则下列判断正确的有( )
 则下列判断正确的有( )
则下列判断正确的有( )
A . 方程  的所有解之和为
的所有解之和为  B . 若直线
B . 若直线  与
与  的图象有且仅有两个公共点,则
的图象有且仅有两个公共点,则  C . 若方程
C . 若方程  恰有四解
恰有四解  ,则
,则 
 D . 若
D . 若  有两正根
有两正根  ,则
,则 
 的所有解之和为
的所有解之和为  B . 若直线
B . 若直线  与
与  的图象有且仅有两个公共点,则
的图象有且仅有两个公共点,则  C . 若方程
C . 若方程  恰有四解
恰有四解  ,则
,则 
 D . 若
D . 若  有两正根
有两正根  ,则
,则 
设向量  =(x﹣1,2),
=(x﹣1,2),  =(1,x),且
=(1,x),且  ⊥
⊥  ,则x=.
,则x=.
 =(x﹣1,2),
=(x﹣1,2),  =(1,x),且
=(1,x),且  ⊥
⊥  ,则x=.
,则x=.
“ab<0”是“方程ax2+by2=c表示双曲线”的( )
A . 充分非必要条件
B . 必要非充分条件
C . 充要条件
D . 既不充分也不必要条件
若  ,
,  ,
,  ,则
,则  的大小关系为( )
的大小关系为( )
 ,
,  ,
,  ,则
,则  的大小关系为( )
的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设 ,
,  ,
,  , 则a,b,c的大小关系为( )
, 则a,b,c的大小关系为( )
 ,
,  ,
,  , 则a,b,c的大小关系为( )
, 则a,b,c的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在 中,三个内角A、B、C所对的边分别为a、b、c,向量
中,三个内角A、B、C所对的边分别为a、b、c,向量 与向量
与向量 夹角的余弦值为
夹角的余弦值为 , 且
, 且 , 则
, 则 的取值范围是.
的取值范围是.
 中,三个内角A、B、C所对的边分别为a、b、c,向量
中,三个内角A、B、C所对的边分别为a、b、c,向量 与向量
与向量 夹角的余弦值为
夹角的余弦值为 , 且
, 且 , 则
, 则 的取值范围是.
的取值范围是.
已知等比数列![]() 的各项均为正数,且
的各项均为正数,且![]() ,
,![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
已知![]() ,且
,且![]() ,若
,若![]() 恒成立,则实数
恒成立,则实数![]() 的值取值范围是( )
的值取值范围是( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]()
已知函数![]() ,对任意的两个实数
,对任意的两个实数![]() ,都有
,都有![]() 成立,且
成立,且![]() ,则
,则![]()
![]() 的值是
的值是
A. 0 B. 1 C. 2006 D. 20062
在![]() 中,
中,![]() 分别为角
分别为角![]() 所对的边,且
所对的边,且![]() ,若
,若![]() ,则
,则![]() __
__
最近更新
- Animals suffered at the hands of Man ___ they were destroyed
- Washing machines made by China have won ______worldwide atte
- 生物兴趣小组的同学们要调查一个池塘中青蛙近几年的个体数量变化情况。他们研究的是生命系统的( ) A.个体水平
- 14.0 g铜银合金与足量某浓度的硝酸反应,将放出的气体与1.12 L(标准状况)氧气混合,通入水中恰好完全吸收,则合金
- “为了适应社会主义改造和社会主义建设的新形势,目前在国家工作中的一个重要任务,是进一步扩大民主生活,开展反对官僚主义的斗
- 在CuO和Fe粉的混合物中,加入一定量的稀硫酸,并微热,当反应停止后,滤出不溶物,并向滤液中插入一枚铁钉,发现铁钉并无任
- 卢梭在《民约论》中说:“立法权是国家的心脏,行政权是国家的大脑,大脑使各个部分运动起。大脑可能陷于麻痹,而人依然活着。一
- 阅读下面的文字,完成问题。 不容忽视的微细尘埃 尘埃无处不有,虽然它们的个体很小,但汇聚起来的威力却不小。据记载,北美大
- (贵州省贵阳二中2010届高三第一学期11月月考) D When I was 16 years old, I made
- “范氏之亡者,百姓有得钟者,欲负而走,则钟大不可负;以椎毁之,钟况然有音,恐人闻之而夺已也,遽掩其耳。恶人闻之,可也;
- 如图所示的几何体的俯视图是() A. B.C. D.
- 据最新报道,科学家发现了如下反应:O2+PtF6 = O2(PtF6),已知O2(PtF6)为离子化合物,其中Pt为+5
- 下列大洲中,既是人口稠密的洲,又是人口增长缓慢的大洲是 A.亚洲 B.大洋洲
- There ________ a sports meeting next week.A.hasB.is going to
- 在当今世界的跨国并购中,产品品牌的变更、兴衰,品牌控制权的转移,新兴品牌的崛起,外国品牌在本土的扩张等,构成了全球经济竞
- — I’d like to go to the cinema with you, Dad. — Sorry, my da
- 在《闯关东》中,从山东龙口港到大连是一条重要的闯关东路线.假设有甲、乙两船同时从.龙口港口出发,甲船路线是龙口—旅顺—大
- 一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示,在A点,物体开始与弹簧接触,到B点时,物体速度为零,然后被
- 一位年轻旅行者叙述自己的生活经验:“小时候,每天走过一个广场上学,可以看到马克思与列宁的铜像,后来铜像拆了,国歌换了,就
- 如图,点A、B、C都在⊙O上,( ) A.40° B.50° C.80°



