高中 数学
若方程x2﹣mx+3=0的两根满足一根大于1,一根小于1,则m的取值范围是( )
A . (2,+∞)
B . (0,2)
C . (4,+∞)
D . (0,4)
已知f(x)=  ,则关于m的不等式f(
,则关于m的不等式f(  )<ln
)<ln  的解集为( )
的解集为( )
 ,则关于m的不等式f(
,则关于m的不等式f(  )<ln
)<ln  的解集为( )
的解集为( )
A . (0,  )
B . (0,2)
C . (﹣
)
B . (0,2)
C . (﹣  ,0)∪(0,
,0)∪(0,  )
D . (﹣2,0)∪(0,2)
)
D . (﹣2,0)∪(0,2)
 )
B . (0,2)
C . (﹣
)
B . (0,2)
C . (﹣  ,0)∪(0,
,0)∪(0,  )
D . (﹣2,0)∪(0,2)
)
D . (﹣2,0)∪(0,2)
设  ,
,  ,
,  ,
,  ,则
,则  ,
,  ,
,  ,
,  的大小关系为( )
的大小关系为( )
 ,
,  ,
,  ,
,  ,则
,则  ,
,  ,
,  ,
,  的大小关系为( )
的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若椭圆C的焦点和顶点分别是双曲线  的顶点和焦点,则椭圆C的方程是.
的顶点和焦点,则椭圆C的方程是.
 的顶点和焦点,则椭圆C的方程是.
的顶点和焦点,则椭圆C的方程是.
如图,四棱锥 中,
中,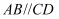 ,
,  ,
,  , 侧面
, 侧面 底面ABCD,E为PC的中点.
底面ABCD,E为PC的中点.
 中,
中,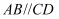 ,
,  ,
,  , 侧面
, 侧面 底面ABCD,E为PC的中点.
底面ABCD,E为PC的中点.
-
(1) 求证:
 平面PCD;
平面PCD;
-
(2) 若
 , 求二面角
, 求二面角 的余弦值.
的余弦值.
执行如图所示的程序框图,若m=4,则输出的结果为( )

A . 1
B .  C . 2
D .
C . 2
D . 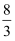
 C . 2
D .
C . 2
D . 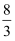
已知全集  ,
,  ,
,  ,则图中阴影部分表示的集合是( )
,则图中阴影部分表示的集合是( )
 ,
,  ,
,  ,则图中阴影部分表示的集合是( )
,则图中阴影部分表示的集合是( ) 
A .  B .
B .  C .
C .  D .
D . 
某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
-
(1)
在给定的坐标系中画出表中数据的散点图;

-
(2) 求出y关于x的线性回归方程;
-
(3) 试预测加工10个零件需要多少时间?(注:
 =
=  ,
,  =
=  ﹣
﹣  )
)
已知向量  ,
,  ,若
,若  ,则实数k的值为( )
,则实数k的值为( )
 ,
,  ,若
,若  ,则实数k的值为( )
,则实数k的值为( )
A . 2
B .  C . 3
D .
C . 3
D . 
 C . 3
D .
C . 3
D . 
过点P(1,2)且倾斜角为45°的直线方程为
如图,在长方形  中,
中, 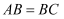 ,E,F分别是
,E,F分别是  ,
,  的中点
的中点  有下列结论:
有下列结论:
 中,
中, 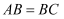 ,E,F分别是
,E,F分别是  ,
,  的中点
的中点  有下列结论:
有下列结论:  ;
;  平面
平面 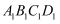 ;
;  与
与  所成角为
所成角为  ;
;  平面
平面  .其中不成立的是
.其中不成立的是 


A .  B .
B .  C .
C .  D .
D . 
已知二面角α-l-β的大小为60°,m,n为异面直线,且m⊥α,n⊥β,则m,n所成的角为( )
A . 30°
B . 60°
C . 90°
D . 120°
已知函数f(x),对任意的x∈[1,+∞),恒有f(2x)=2f(x)成立,且当x∈[1,2)时,f(x)=2﹣x.则方程 在区间[1,100]上所有根的和为 .
在区间[1,100]上所有根的和为 .
 在区间[1,100]上所有根的和为 .
在区间[1,100]上所有根的和为 .
如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.

-
(1) 求证:平面BC1D⊥平面ACC1A1;
-
(2) 求三棱锥C﹣BC1D的体积.
函数f(x)=log3(x2﹣2x﹣3)的单调增区间为
在正方体ABCD﹣A1B1C1D1中,E是棱A1B1的中点,则A1B与D1E所成角的余弦值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知不等式 对任意
对任意 都成立,则实数m的取值范围是( )
都成立,则实数m的取值范围是( )
 对任意
对任意 都成立,则实数m的取值范围是( )
都成立,则实数m的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
有A,B,C,D四个城市,它们各有一个著名的旅游景点,依次记为a,b,c,d,把A,B,C,D和a,b,c,d分别写成左右两列,现在一名旅游爱好者随机用4条线把左、右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分。
(1)求该爱好者得分的分布列;
(2)求所得分的数学期望。
在△![]() 中,若
中,若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
若函![]() 数
数![]() 为奇函数,则
为奇函数,则![]() .
.
最近更新
- 在一定条件下,氯气与碘单质以等物质的量进行反应,可得到一种红棕色液体ICl,ICl有很强的氧化性,ICl跟Zn、H2O反
- 如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取
- 小明发现野营篝火的火焰很小,便将木柴架空火焰就大了,他这样做主要是为了 A.降低木柴的着火点
- 下列方程中有两个不相等实数根的方程是() A.x2﹣2x+2=0 B. =﹣1 C.x2﹣3x+
- 镓元素的单质是半导体材料。下列有关说法错误的是( ) A.镓的核电荷数是31 B. 镓原子核外电子数是31
- 《论语》十二章(节选) ①子曰:“学而时习之,不亦说乎?有朋自远方来,不亦乐乎?人不知而不愠,不亦君子乎?” ②曾子曰:
- 臭氧层保护是当今全球最重要的环保议题之一。图2反映了9月份30°S~80°S平流层臭氧总量多年变化状况。读图2回答第1-
- 图9是安装在列车车厢之间的摩擦缓冲器结构图,图中①和②为楔块,③和④为垫块,楔块与弹簧盒、垫块间均有摩擦,在车厢相互撞击
- 小明从眼镜上取下一块镜片,透过镜片观看邮票上的文字(如图所示).小明用的镜片是_______透镜,所成的是_______
- Thebig desk toomuch room. Please take it away.
- 下列加线字与“函封之”中的“函”用法不同的一项是 () A.君为我呼入,吾得兄事之 B.秦伯说,与郑人盟 C.项伯亦拔剑
- 已知实数x,y满足的图象与坐标轴所围成的封闭图形的内部的概率为 A.
- 关于运动的性质,以下说法中正确的是()A. 曲线运动一定是变速运动 B. 变速运动一定是曲线运动 C. 曲线运动一定是变
- 我国最长的内流河是( ) A、长江 B、黄河 C、塔里木河 D、珠江
- 一定条件下的密闭容器中: 4NH3(g)+5O2(g)4NO(g)+6H2O(g) ΔH=-905.9 kJ· mol
- 右图表示绿色植物体内某些代谢过程中物质的变化,a、b、c分别表示不同的代谢过程。以下表述正确的是( ) A.
- 同温同压下,两种气体的体积如果不相同,请你推测其主要的原因是A.气体的分子大小不同 B.气体分子的物质的量不
- Madane curie’s _____ encouraged many women to study science
- 数列12,12+22,12+22+32,…,12+22+…+n2,…的通项公式为A.an=
- 下列关于国家的说法,正确的是( ) ①自从人类出现就产生了国家 ②政治性是国家的根



