高中 数学
为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车  辆,混合动力型公交车
辆,混合动力型公交车  辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加 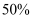 ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入  辆.设
辆.设  、
、  分别为第
分别为第  年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设  、
、  分别为
分别为  年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
 辆,混合动力型公交车
辆,混合动力型公交车  辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加 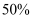 ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入  辆.设
辆.设  、
、  分别为第
分别为第  年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设  、
、  分别为
分别为  年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
-
(1) 求
 、
、  ,并求
,并求  年里投入的所有新公交车的总数
年里投入的所有新公交车的总数  ;
;
-
(2) 该市计划用
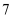 年的时间完成全部更换,求
年的时间完成全部更换,求  的最小值.
的最小值.
在数列中,主要是两大问题,一是:求数列的通项;二是:求和.已知数列{an}的前n项和为Sn , 且Sn+an=2﹣  .
.
 .
.
-
(1) 写出a1 , a2 , a3 , a4的值(只写结果),并猜想{an}的通项公式;
-
(2) 用数学归纳法,证明你的猜想是正确的.(这种求数列通项的方法,称之为数学归纳法)
已知函数  .
.
 .
. (Ⅰ)若  ,求函数
,求函数  的定义域和值域;
的定义域和值域;
(Ⅱ)若函数  的定义域为
的定义域为  ,值域为
,值域为  ,求实数
,求实数 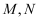 的值.
的值.
下列命题是真命题的是( )
A . 若 , 则x=2
B . 若x=y,则
, 则x=2
B . 若x=y,则 C . 若
C . 若 , 则x=y
D . 若x>y,则|x|>|y|
, 则x=y
D . 若x>y,则|x|>|y|
 , 则x=2
B . 若x=y,则
, 则x=2
B . 若x=y,则 C . 若
C . 若 , 则x=y
D . 若x>y,则|x|>|y|
, 则x=y
D . 若x>y,则|x|>|y|
在平行四边形  中,
中,  ,
,  ,
,  ,
,  是
是  的中点,则
的中点,则  .
.
 中,
中,  ,
,  ,
,  ,
,  是
是  的中点,则
的中点,则  .
.
已知集合  ,
,  ,全集
,全集  ,若
,若  ,则实数
,则实数  的取值范围为.
的取值范围为.
 ,
,  ,全集
,全集  ,若
,若  ,则实数
,则实数  的取值范围为.
的取值范围为.
已知函数f(x)=a(x+ )﹣|x﹣
)﹣|x﹣ |(x>0)a∈R.
|(x>0)a∈R.
 )﹣|x﹣
)﹣|x﹣ |(x>0)a∈R.
|(x>0)a∈R.(1)若a= , 求y=f(x)的单调区间;
, 求y=f(x)的单调区间;
(2)若关于x的方程f(x)=t有四个不同的解x1 , x2 , x3 , x4 , 求实数a,t应满足的条件;
(3)在(2)条件下,若x1 , x2 , x3 , x4成等比数列,求t用a表示.
设函数 , 若
, 若 无最大值,则实数
无最大值,则实数 的取值范围是.
的取值范围是.
 , 若
, 若 无最大值,则实数
无最大值,则实数 的取值范围是.
的取值范围是.
某参考辅导书上有这样的一个题:△  中,
中,  与
与  方程
方程 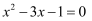 的两个根,则
的两个根,则  的值为( )
的值为( )
 中,
中,  与
与  方程
方程 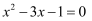 的两个根,则
的两个根,则  的值为( )
的值为( ) A.  B.
B.  C.
C.  D.
D. 
你对这个题目的评价是.(用简短语句回答)
设 , 则()
, 则()
 , 则()
, 则()
A . a<c<b
B . b<c<a
C . a<b<c
D . b<a<c
如图,在棱长为1的正方体  中,
中,  为线段
为线段  的中点,
的中点,  为线段
为线段  的中点.
的中点.
 中,
中,  为线段
为线段  的中点,
的中点,  为线段
为线段  的中点.
的中点. 
-
(1) 求直线
 到平面
到平面  的距离;
的距离;
-
(2) 求平面
 与平面
与平面  所成锐二面角的余弦值.
所成锐二面角的余弦值.
满足条件  ∪{1}={1,2,3}的集合
∪{1}={1,2,3}的集合  的个数是( )
的个数是( )
A . 1
B . 2
C . 3
D . 4
在等差数列{an}中,a1+a9=10,则a5的值为( )
A . 5
B . 6
C . 8
D . 10
已知圆 M与圆N:(x﹣  )2+(y+
)2+(y+  )2=r2关于直线y=x对称,且点D(﹣
)2=r2关于直线y=x对称,且点D(﹣  ,
, 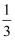 )在圆M上.
)在圆M上.
 )2+(y+
)2+(y+  )2=r2关于直线y=x对称,且点D(﹣
)2=r2关于直线y=x对称,且点D(﹣  ,
, 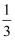 )在圆M上.
)在圆M上.
-
(1) 判断圆M与圆N的公切线的条数;
-
(2) 设P为圆M上任意一点,A(﹣1,
 ),B(1,
),B(1,  ),P,A,B三点不共线,PG为∠APB的平分线,且交AB于G,求证:△PBG与△APG的面积之比为定值.
),P,A,B三点不共线,PG为∠APB的平分线,且交AB于G,求证:△PBG与△APG的面积之比为定值.
已知  为各项都是正数的等比数列,若
为各项都是正数的等比数列,若  ,则
,则  .
.
 为各项都是正数的等比数列,若
为各项都是正数的等比数列,若  ,则
,则  .
.
德国著名数学家狄利克雷在数学领域成就显著,是解析数论的创始人之一,以其名命名的函数 成为狄利克雷函数,则关于
成为狄利克雷函数,则关于![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.![]()
B.函数![]() 是偶函数
是偶函数
C.任意一个非零有理数![]() ,
,![]() 对任意
对任意![]() 恒成立
恒成立
D.存在三个点![]() ,使得
,使得![]() 为等边三角形
为等边三角形
已知复数![]() 与
与![]() 均为纯虚数,则
均为纯虚数,则![]() 。
。
若函数![]() 在区间
在区间![]() 上是减函数,则函数
上是减函数,则函数![]() 的增区间为____________________
的增区间为____________________
函数![]() 的图象如图,其中a,b为常数,则下列结论正确的是( )
的图象如图,其中a,b为常数,则下列结论正确的是( )

A.a>1,b<0 B.a>1,b>0 C.0<a<1,b>0 D.0<a<1,b<0
对于二项式(1-x)10, 求:
(1)展开式的中间项是第几项?写出这一项;
(2)求展开式中除常数项外,其余各项的系数和;
(3)写出展开式中系数最大的项.
最近更新
- Health is themost important thing in the world. Nothing is m
- 下列描述的运动中可能的有( ) A.速度变化很大,加速度为零 B.速度变化方向
- 我国戈壁大沙漠中植物稀少,起决定作用的主要非生物因素是()A.阳光B.温度C.水分D.空气
- 下列与细胞分裂有关的叙述中,不正确的是( ) A.蛙的受精卵的
- 关于原子、分子、离子的说法中,错误的是( ) A.原子不能直接构成物质 B.分子可以保持物质的化学性质 C.原子的质量
- 读美国本土图,回答:(10分)(1)从图中可看出,与美国陆地相邻的国家是_________和 。 (2)
- Ifyou are to get up early and do exercises every morning,itw
- 将阻值为5Ω的电阻接到内阻不计的交流电源上,电源电动势随时间变化的规律如图所示。下列说法正确的是 A.电路中交变电流的频
- 阅读短文,回答文后问题 树木在低温时细胞受伤,会造成枝条电阻发生变化.用电阻测量法可以鉴别树木的耐寒能力.实验时,取某
- 若函数的导函数在区间上的图象关于直线对称,则函数在区间上的图象可能是( ) A.①
- 下列关于基因工程的叙述中正确的是 A、基因工程经常以抗菌素抗性基因为目的基因 B、细菌质粒是基因工程常用的运载体
- “曹州(菏泽古称曹州)牡丹甲天下”,家住北京的玲玲利用周末乘火车去菏泽看牡丹,并顺利返回.在整个过程中,玲玲使用了四幅地
- 现有0.1 mol某有机物A,在8.96 L O2中充分燃烧后,气体的体积变为6.72 L,通过碱石灰吸收后剩余2.24
- 线段在平面内,则直线与平面的位置关系是( ) A. B. C.由线段的长短而定 D.以上都不对
- 某学生量取液体,视线与液体凹液面的最低处相平,读数为30mL,将液体倒出一部分后,仰视读数为20mL,则该同学实际倒出的
- 硅被誉为无机非金属材料的主角,下列物品用到硅单质的是( ) A.光导纤维 B.计算机芯片
- 糖类、脂肪和蛋白质是维持人体生命活动所必需的三大营养物质。以下叙述正确的是( )A.植物油不能发生水解反应
- 阅读下面的文字,完成后面题目。 城乡文化的交融 过去,社会文化同生活方式一样,也可以分为城市文化和乡村文化,两者之间似乎
- 规范操作是实验安全和成功的保证。按右图所示做细铁丝在氧气中燃烧的实验时,若事先未在瓶底铺一层细沙或装入少量的水,可能出现
- CoxFe3-xO4磁粉是一种比较好的高矫顽力磁粉。工业上以FeSO4为原料制备CoxFe3-xO4的主要步骤如下: F



