高中 数学
已知幂函数  的图象经过点
的图象经过点  ,则
,则  的值为.
的值为.
 的图象经过点
的图象经过点  ,则
,则  的值为.
的值为.
已知数列  满足
满足  ,
,  .
.
 满足
满足  ,
,  .
.
-
(1) 证明:数列
 为等差数列;
为等差数列;
-
(2) 设
 ,求数列
,求数列  的前
的前  项和
项和  .
.
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则此双曲线的离心率为( )
的焦点重合,则此双曲线的离心率为( )
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则此双曲线的离心率为( )
的焦点重合,则此双曲线的离心率为( )
A . 2
B .  C . 3
D . 4
C . 3
D . 4
 C . 3
D . 4
C . 3
D . 4
为了测量河对岸两点 间的距离,现在沿岸相距
间的距离,现在沿岸相距 的两点
的两点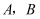 处分别测得
处分别测得 ,
,  , 则
, 则 间的距离为( )
间的距离为( )
 间的距离,现在沿岸相距
间的距离,现在沿岸相距 的两点
的两点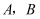 处分别测得
处分别测得 ,
,  , 则
, 则 间的距离为( )
间的距离为( )
A .  B . 2
C .
B . 2
C .  D . 4
D . 4
 B . 2
C .
B . 2
C .  D . 4
D . 4
若  ,
,  满足约束条件
满足约束条件  ,则
,则  的最大值为.
的最大值为.
 ,
,  满足约束条件
满足约束条件  ,则
,则  的最大值为.
的最大值为.
已知扇形OAB的圆心角为120°,半径长为6,求:
(1)弧AB的长;
(2)弓形AOB的面积.
某射击选手射击目标两次,第一次击中目标的概率是 , 两次均击中目标的概率是
, 两次均击中目标的概率是 .则该选手在第一次射击已经击中目标的前提下,第二次射击也击中目标的概率是( )
.则该选手在第一次射击已经击中目标的前提下,第二次射击也击中目标的概率是( )
 , 两次均击中目标的概率是
, 两次均击中目标的概率是 .则该选手在第一次射击已经击中目标的前提下,第二次射击也击中目标的概率是( )
.则该选手在第一次射击已经击中目标的前提下,第二次射击也击中目标的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列函数f(x)中,满足“对任意x1、x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)的是( )
A . f(x)= B . f(x)=(x﹣1)2
C . f(x)=ex
D . f(x)=ln(x+1)
B . f(x)=(x﹣1)2
C . f(x)=ex
D . f(x)=ln(x+1)
 B . f(x)=(x﹣1)2
C . f(x)=ex
D . f(x)=ln(x+1)
B . f(x)=(x﹣1)2
C . f(x)=ex
D . f(x)=ln(x+1)
已知集合 ,
,  , 则
, 则 ( )
( )
 ,
,  , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若  ,则a2=( )
,则a2=( )
 ,则a2=( )
,则a2=( )
A . 112
B . 56
C . 28
D . 12
数列  的通项公式是
的通项公式是  ,那么它的前n项和最大时的
,那么它的前n项和最大时的  的值是.
的值是.
 的通项公式是
的通项公式是  ,那么它的前n项和最大时的
,那么它的前n项和最大时的  的值是.
的值是.
过点  的圆
的圆  与直线
与直线  相切于点
相切于点  ,则圆
,则圆  的方程为.
的方程为.
 的圆
的圆  与直线
与直线  相切于点
相切于点  ,则圆
,则圆  的方程为.
的方程为.
已知函数f(x)=asinx+bcosx(a,b为常数,a≠0,x∈R)在x=  处取得最大值,则函数y=f(x+
处取得最大值,则函数y=f(x+  )是( )
)是( )
 处取得最大值,则函数y=f(x+
处取得最大值,则函数y=f(x+  )是( )
)是( )
A . 奇函数且它的图象关于点(π,0)对称
B . 奇函数且它的图象关于点(  ,0)对称
C . 偶函数且它的图象关于点(
,0)对称
C . 偶函数且它的图象关于点(  ,0)对称
D . 偶函数且它的图象关于点(π,0)对称
,0)对称
D . 偶函数且它的图象关于点(π,0)对称
 ,0)对称
C . 偶函数且它的图象关于点(
,0)对称
C . 偶函数且它的图象关于点(  ,0)对称
D . 偶函数且它的图象关于点(π,0)对称
,0)对称
D . 偶函数且它的图象关于点(π,0)对称
选修4—5:不等式选讲
已知函数![]()
(1)求不等式![]() 的解集;
的解集;
(2)若关于x的不等式![]() 的解集非空,求实数
的解集非空,求实数![]() 的取值范围.
的取值范围.
如图,有一块半椭圆形钢板,其长半轴长为![]() ,短半轴长为
,短半轴长为![]() .计划将此钢板切割成等腰梯形的形状,下底
.计划将此钢板切割成等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,记
的端点在椭圆上,记![]() ,梯形面积为
,梯形面积为![]() .
.
(Ⅰ)求面积![]() 以
以![]() 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(Ⅱ)求面积![]() 的最大值.
的最大值.

已知P,A,B,C是平面内四点,且![]() +
+![]() +
+![]() =
=![]() ,则下列向量一定共线的是( )
,则下列向量一定共线的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]() C.
C.![]() 与
与![]() D.
D.![]() 与
与![]()
2log210+log20.04
椭圆![]() 的焦距为
的焦距为![]() ,则
,则![]() 的值等于( )
的值等于( )
A. ![]() 或
或![]() B.
B. ![]() 或
或![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
已知函数![]() 的最小正周期为
的最小正周期为![]() .
.
![]() 求
求![]() 的值;
的值;
![]() 中,角A,B,C的对边分别为a,b,c,
中,角A,B,C的对边分别为a,b,c,![]() ,
,![]() ,
,![]() 面积
面积![]() ,求b.
,求b.
给出下面五个命题,不正确的是:
①若向量![]() 、
、![]() 满足
满足![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() 在
在![]() 上的投影等于
上的投影等于![]() ;②若等比数列
;②若等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 、
、![]() 、
、![]() 也成等比数列;
也成等比数列;
③常数列既是等差数列,又是等比数列;
④若向量![]() 与
与![]() 共线,则存在唯一实数
共线,则存在唯一实数![]() ,使得
,使得![]() 成立;
成立;
⑤在正项等比数列![]() 中,若
中,若![]() ,则
,则![]() .
.
最近更新
- 在恒容密闭容器中存在下列平衡:CO(g)+H2O(g)CO2(g)+H2(g)。CO2(g)的平衡物质的量浓度c(CO2
- 图画是某一时期的壁画作品,它发生于 A.抗美援朝时期 B.“大跃进”运动时期C.“”期间
- 若l000张奖券中有200张可以中奖,则从中任抽1张能中奖的概率为__________.
- 二、现代文阅读 阅读下文,完成下列各题。 安徒生与他的童话世界 我们可以通过两条不同的道路进入汉斯·克里斯蒂安·安徒生的
- ---______ you ____ (see) the film yet?---Yes, I _______ (se
- When can you ______ the book? A. read finishing B. fini
- 设函数f(x)=2x3-3(a+1)x2+6ax+8,其中a∈R.(1)若f(x)在x=3处取得极值,求常数a的值;(2
- 已知,,, 则=____▲ ___.
- 种群在理想环境中,呈“J”型曲线增长(如下图甲);在有环境阻力条件下,呈“S”型曲线增长(如下图乙)。下列有关种群增长曲
- 类推是一种重要的学习方法,但如果不具体问题具体分析就会产生错误的结论.下列类推结论错误的是() ①CO能与Fe2O3反应
- 读下图,完成15、16题。15、该国储量、产量都居世界前列的矿产资源是( ) A.铁
- 如图,直线 l 1 ∥ l 2,点 A 在直线 l 1上,以点 A 为圆心,适当长度为半径画弧,分别交直线 l 1, l
- 在中国近代的某个时期,激进的知识分子及青年学生认为,拯救中国之道在于全面否定传统。为此,他们提倡 A、中体西用
- 在下图的四个种群年龄分布类型中,哪一类型种群灭绝的可能性最大
- 将22.4g铁粉逐渐加入到含HNO3 0.8mol的硝酸中,反应生成的气体的物质的量(x)(假设HNO3的还原产物只有N
- 下列化合物与小苏打溶液反应,没有气体或沉淀生成的是() A.烧碱 B.硫酸氢钠
- 阅读下文,完成第16-20题。(21分) 钓鱼诸岛 ①钓鱼诸岛由11个无人岛组成,包括钓鱼岛、黄尾屿、赤尾屿、北小岛、南
- The box is . Can you move it to another place? A.
- 新世纪以来指导“三农”工作的第7个中央一号文件2010年1月31日由新华社受权发布。这个题为《中共中央、国务院关于加大
- 阅读下面一首诗,并进行鉴赏: 长歌行 青青园中葵,朝露待日晞。 阳春布德泽,万物生光辉。 常恐秋节至,焜黄华叶衰。 百川



