高中 数学
已知函数  .
.
 .
.
-
(1) 当
 时,求函数
时,求函数  的单调区间;
的单调区间;
-
(2) 函数
 在
在  上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
已知 .
.
 .
.
-
(1) 若
 , 解不等式
, 解不等式 ;
;
-
(2) 若
 时,
时, 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
点  ,
,  是圆
是圆  上的不同两点,且点
上的不同两点,且点  ,
,  关于直线
关于直线  对称,则该圆的半径等于( )
对称,则该圆的半径等于( )
 ,
,  是圆
是圆  上的不同两点,且点
上的不同两点,且点  ,
,  关于直线
关于直线  对称,则该圆的半径等于( )
对称,则该圆的半径等于( )
A .  B .
B .  C . 1
D . 3
C . 1
D . 3
已知函数f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
-
(1) 令g(x)为f(x)的导函数,求g(x)单调区间;
-
(2) 已知函数f(x)在x=1处取得极大值,求实数a取值范围.
数列  是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前  项和为
项和为  ,
,  ,
,  .等差数列
.等差数列  的前
的前  项和为
项和为  ,且
,且  ,
,  .
.
 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前  项和为
项和为  ,
,  ,
,  .等差数列
.等差数列  的前
的前  项和为
项和为  ,且
,且  ,
,  .
.
-
(1) 求
 和
和  的通项公式;
的通项公式;
-
(2) 是否存在大于2的正整数
 ,使得
,使得  ,
,  ,
,  成等比数列?若存在,求出
成等比数列?若存在,求出  的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数f(x)=x﹣alnx(a∈R)
-
(1) 当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程.
-
(2) 求函数f(x)的极值.
命题“  ”的否定是.
”的否定是.
 ”的否定是.
”的否定是.
函数 
 的部分图像如图所示,若
的部分图像如图所示,若 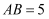 ,点A的坐标为
,点A的坐标为  ,若将函数
,若将函数  向右平移
向右平移  个单位后函数图象关于y轴对称,则m的最小值为( )
个单位后函数图象关于y轴对称,则m的最小值为( )

 的部分图像如图所示,若
的部分图像如图所示,若 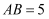 ,点A的坐标为
,点A的坐标为  ,若将函数
,若将函数  向右平移
向右平移  个单位后函数图象关于y轴对称,则m的最小值为( )
个单位后函数图象关于y轴对称,则m的最小值为( ) 
A .  B .
B . 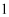 C .
C .  D .
D . 
 B .
B . 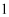 C .
C .  D .
D . 
已知x与y之间的一组数据:
x | 0 | 1 | 2 | 3 |
y | 1 | 3 | 5 | 7 |
则y与x的线性回归方程为y=bx+a必过点( )
A . (2,2)
B . (1.5,0)
C . (1.5,4)
D . (1, 2)
用反证法证明“若a,b,c<3,则a,b,c中至少有一个小于1”时,“假设”应为( )
A . 假设a,b,c至少有一个大于1
B . 假设a,b,c都大于1
C . 假设a,b,c至少有两个大于1
D . 假设a,b,c都不小于1
已知函数  ,若关于
,若关于  的方程
的方程  有5个实数不同的解,则实数
有5个实数不同的解,则实数  的取值范围是( )
的取值范围是( )
 ,若关于
,若关于  的方程
的方程  有5个实数不同的解,则实数
有5个实数不同的解,则实数
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知sinα=2cosα,则  =( )
=( )
 =( )
=( )
A .  B .
B .  C . 2
D .
C . 2
D . 
 B .
B .  C . 2
D .
C . 2
D . 
已知函数f(x)=  ,若关于x的不等式f(x2﹣2x+2)<f(1﹣a2x2)的解集中有且仅有三个整数,则实数a的取值范围是( )
,若关于x的不等式f(x2﹣2x+2)<f(1﹣a2x2)的解集中有且仅有三个整数,则实数a的取值范围是( )
 ,若关于x的不等式f(x2﹣2x+2)<f(1﹣a2x2)的解集中有且仅有三个整数,则实数a的取值范围是( )
,若关于x的不等式f(x2﹣2x+2)<f(1﹣a2x2)的解集中有且仅有三个整数,则实数a的取值范围是( )
A . [﹣  ,﹣
,﹣  )∪(
)∪(  ,
,  ]
B . (
]
B . (  ,
,  ]
C . [﹣
]
C . [﹣  ,﹣
,﹣  )∪(
)∪(  ,
,  ]
D . [﹣
]
D . [﹣  ,﹣
,﹣  )∪(
)∪(  ,
,  ]
]
 ,﹣
,﹣  )∪(
)∪(  ,
,  ]
B . (
]
B . (  ,
,  ]
C . [﹣
]
C . [﹣  ,﹣
,﹣  )∪(
)∪(  ,
,  ]
D . [﹣
]
D . [﹣  ,﹣
,﹣  )∪(
)∪(  ,
,  ]
]
已知函数  的图像向右平移
的图像向右平移  个单位长度得到
个单位长度得到  的图像,
的图像,  图像关于原点对称,
图像关于原点对称,  的相邻两条对称轴的距离是
的相邻两条对称轴的距离是  .
.
 的图像向右平移
的图像向右平移  个单位长度得到
个单位长度得到  的图像,
的图像,  图像关于原点对称,
图像关于原点对称,  的相邻两条对称轴的距离是
的相邻两条对称轴的距离是  .
.
-
(1) 求
 在
在  上的增区间;
上的增区间;
-
(2) 若
 在
在  上有两解,求实数
上有两解,求实数  的取值范围.
的取值范围.
从1,2,3,4,5,6六个数字中任选3个后得到一个由这三个数组成的最小三位数,则可以得到多少个不同的这样的最小三位数?
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2a,AB=a,F为CD的中点.

(1)求证:AF⊥平面CDE;
(2)求异面直线AC,BE所成角的余弦值;
(3)求面ACD和面BCE所成锐二面角的大小.
![]() 是两条不同的直线,
是两条不同的直线,![]() 垂直于平面
垂直于平面![]() ,则“
,则“![]() ”是“
”是“![]() 的 ( ) A.充分而不必要条件 B.
的 ( ) A.充分而不必要条件 B.![]() 必要而不充分条件
必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
已知正实数x,y,且x2+y2=1,若f(x,y)=![]() ,则f(x,y)的值域为 .
,则f(x,y)的值域为 .
A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为 ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为

A. B.
B.  C.
C.  D.
D. 
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为
A.
设函数 在
在 上存在导函数
上存在导函数 ,
, ,有
,有 ,在
,在 上有
上有 ,若
,若 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A. B.
B.  C.
C.  D.
D. 
A.
最近更新
- 某项科学研究,以45分钟为1个时间单位,并记每天上午10时为0,10时以前记为负,10时以后记为正,例如,9:15记为-
- 二战后,西方主要资本主义国家普遍采取国家干预经济的政策。这一政策的理论依据来自A.亚当·斯密 B.凯恩斯
- 下列说法中不正确的是( ) A.根据速度定义式,当Δt非常非常小时,就可以表示物体在t时刻的瞬时速度,该定义应用了极
- 在实验室粗盐的提纯实验中,玻璃棒的使用不具有的作用是A.在溶解过程中搅拌 B. 在蒸发过程中搅拌 C.在
- 如图,▱ABCD中,下列说法一定正确的是()A.AC=BD B.AC⊥BD C.AB=CD D.AB=B
- 读下面的“1991~2004年中的五年世界人口主要统计指标”表表中①、②、③依次是 ( ) A.2.6 0
- 下列动物中,不属于鸟类的是 ( )
- 22.在下面一段文字的横线处补写恰当的语句,使整段文字语意完整连贯,内容贴切,逻辑严密,每处不超过10个字。 古人历经几
- 有人指出:每位人大代表都应发挥“一盏灯”的作用,敢于照亮自己,也乐于照亮别人,要勇立潮头,会当经济发展的参谋员,勇当经济
- 有人认为:“经济发展是文化发展的基础,文化发展始终与经济的发展亦步亦趋。”上述观点( )A、承认了文化对经济的决
- 将红、黑、白三个棋子放入如图所示的小方格内,每格内只 放一个,且3个棋子既不同行也不同列,则不同的放法有
- (4分)如图所示,实线为电场线,虚线为等势线,且相邻两等势间的电势差相等,一正电荷在等势线U3上时,具有动能20J,它运
- 从地转偏向力考虑,理想状态下,下列示意图中(空心箭头表示水流初始运动方向,虚线箭头表示水流实际运动方向),能正确表示北半
- 下列港口中分布在北冰洋沿岸并且为不冻港的是( ) A.摩尔曼斯克 B.苏维埃港 C.圣彼
- 如图A-3所示,一木块被两块木板夹在中间静止不动,在两侧对木板施加水平方向的大小均为N的力,已知木块的质量为m.则(1)
- The girl isfrom_________ and she is________ A.China;Chinese
- 如下图所示,肺炎双球菌转化实验中,在培养有R型细菌的A、B、C、D四支试管中,一次分别加入从S型细菌中提取的DNA、DN
- 将圆柱体B竖立在圆柱形容器A的水平底面上,圆柱体B对容器A底面的压强为0p。向容器A内缓慢注水,记录注入水的质量m和所对
- 下列说法中错误的是: A.重力对物体所做的功只跟起点和终点位置有关,跟物体的运动路径无关; B.摩擦力对物体做功
- 在海上或沙漠上,有时会看到高楼大厦,热闹的市场,实际大海、沙漠上并没有这些楼市,这种现象叫“海市蜃楼”,出现“海市蜃楼”



