高中 数学
 中,已知
中,已知  ,直线
,直线  经过点
经过点  .
. (Ⅰ)若直线  :
:  与线段
与线段  交于点
交于点  ,且
,且  为△
为△  的外心,求△
的外心,求△  的外接圆的方程;
的外接圆的方程;
(Ⅱ)若直线  方程为
方程为  ,且△
,且△  的面积为
的面积为  ,求点
,求点  的坐标.
的坐标.

 ,乙每次投中的概率为
,乙每次投中的概率为  ,每人分别进行三次投篮.
,每人分别进行三次投篮. (I)记甲投中的次数为  ,求
,求  的分布列及数学期望
的分布列及数学期望  ;
;
(Ⅱ)求乙至多投中2次的概率;
(Ⅲ)求乙恰好比甲多投进2次的概率.
①若
 ,则
,则
②若
 且
且 则
则
③若
 ,则
,则
④若
 ,则
,则
其中正确命题的个数为( )
 =2,则x2+
=2,则x2+  =2”类比推出“若x-
=2”类比推出“若x-  =2,则x2+
=2,则x2+  =2”
C . “实数a,b,c满足运算(ab)c=a(bc)”类比推出“平面向量a,b,c满足运算(a·b)c=a(b.c)”
D . “正方形的内切圆切于各边的中点”类比推出“正方体的内切球切于各面的中心”
=2”
C . “实数a,b,c满足运算(ab)c=a(bc)”类比推出“平面向量a,b,c满足运算(a·b)c=a(b.c)”
D . “正方形的内切圆切于各边的中点”类比推出“正方体的内切球切于各面的中心”
 则△ABC的形状是 ()
则△ABC的形状是 ()
 为定义在
为定义在  上的奇函数.
上的奇函数. (Ⅰ)求  的解析式;
的解析式;
(Ⅱ)判断  在定义域
在定义域  上的单调性,并用函数单调性定义给予证明;
上的单调性,并用函数单调性定义给予证明;
(Ⅲ)若关于  的方程
的方程  在
在  上有解,求实数
上有解,求实数  的取值范围.
的取值范围.
如图,在正方体ABCD﹣A1B1C1D1中,若平面A1BCD1上一动点P到AB1和BC的距离相等,则点P的轨迹为( )

 , 则下列结论正确的为( )
, 则下列结论正确的为( )
 ,
,  ,
,  是等差数列
B . 数列
是等差数列
B . 数列 ,
,  ,
,  是等差数列
C . 数列
是等差数列
C . 数列 ,
,  ,
,  是等比数列
D . 数列
是等比数列
D . 数列 ,
,  ,
,  是等比数列
是等比数列
 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意  都有
都有  ,当
,当  ,且
,且  时,
时,  ,给出如下命题:
,给出如下命题: ①  ;②直线
;②直线  是函数
是函数  的图象的一条对称轴;③函数
的图象的一条对称轴;③函数  在
在  上为增函数;④函数
上为增函数;④函数  在
在  上有四个零点.其中所有正确命题的序号为( )
上有四个零点.其中所有正确命题的序号为( )
 AB=3,则△SED面积的最小值为.
AB=3,则△SED面积的最小值为.
 的顶点与原点
的顶点与原点 重合,始边与
重合,始边与 轴的非负半轴重合,它的终边过点
轴的非负半轴重合,它的终边过点 , 且点
, 且点 在圆
在圆 :
: 上.
上.
-
(1) 若
 点的横坐标为-3,求
点的横坐标为-3,求 的值;
的值;
-
(2) 若角
 满足
满足 , 求
, 求 的最大值.
的最大值.
(2012辽宁理)电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;

将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(Ⅰ)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性别
列联表,并据此资料你是否认为“体育迷”与性别
有关?

(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽
样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望![]() 和方差
和方差![]() .
.
附:![]()
![]()
若曲线![]() 在点(0, b)处的
在点(0, b)处的![]() 切线方程是
切线方程是![]() , 则( )
, 则( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
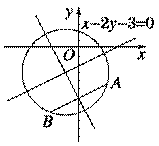
已知一圆经过点A(2,-3)和B(-2,-5),且圆心C在直线l:x-2y-3=0上,
(1)求此圆的标准方程;
(2)判断点M1(0,1),M2(2,-5)与该圆的位置关系.
已知集合![]() ,其中
,其中![]() ,将
,将![]() (
(![]() )中所有不同值的个数记为L(A)。
)中所有不同值的个数记为L(A)。
(I)设集合![]() ,
,![]() ,求L(P),L(Q);
,求L(P),L(Q);
(II)设集合![]() ,求L(B)的值(用含n的式子表示);
,求L(B)的值(用含n的式子表示);
(III)求L(A)的最小值(用含n的式子表示)
已知函数 若关于
若关于![]() 的方程
的方程![]() 有两个不等的实根,则实数
有两个不等的实根,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
若圆C1:![]() 与圆C2:
与圆C2:![]() 相切,则
相切,则![]() 等于( )
等于( )
A.16 B.7 C.﹣4或16 D.7或16
- 以下各种尾气吸收装置中,适合吸收易溶性气体,而且能防倒吸的是( )
- .若集合,或,则 A. B. C. D.
- 下列关于电容器的说法,正确的是A.电容器带电量越多,电容越大 B.电容器两板电势差越小,电容越大 C.电容器的电容与
- 在一位埃及法老的陵墓里,发现很多神秘的符号,考古学家认为这是种古老的文字,它应该是( ) A、象形文字 B、楔
- 图示意我国近几年的劳动年龄人口变化及未来预测。读图回答下列各题。2000~2020年,我国 ( ) A
- “纸火锅”(如图)是用纸张代替金属材料做容器盛放汤料,当酒精燃烧时纸张不会燃烧.对此现象,下列解释合理的是 A.纸张不是
- 冬天,牙医常把检查口腔的小镜子放在酒精灯上烤一烤后才伸进口腔内进行检查。这样做的主要目的是:A. 防止接触口腔时病人感到
- “君主近臣,代起执政,品位既高,退居闲曹。”是汉武帝为加皇权而实行的一项措施。对这一措施的正确叙述应是( )A.布
- 要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在
- 阅读下面这首宋词,然后回答问题(1)—(2)。 卜算子•送鲍浩然之浙东 王观 水是眼波横,山是眉峰聚。欲问行人去那边
- 依次填入横线上最恰当的一组词语是 ( ) ①学校决定,凡国家规定休息的国庆长假,高一、高二学
- 下列是应用动物细胞工程技术获取单克隆抗X抗体的具体操作步骤,其中对单克隆抗体制备的相关叙述中不正确的是() ①从患骨髓瘤
- 用某仪器测量一液体体积时,平视时读数为nml, 仰视时读数为xml, 俯视时读数为yml,若y >n> x,
- 改革开放30多年来,中国人民的生存权和发展权实现了历史性改善,政治权利得到有效保障,基本文化权益得到更好的维护和实现,这
- 青蛙被称为两栖动物的主要原因是( ) A.幼体只能生活在水中,成体只能生活在陆地上 B.在水中生殖,在陆
- 已知,则( ) A. B. C. D.
- 下列各数中:+5、、、2、、、0、-负有理数有 ( ) A.2个 B.3个 C.4个
- 如图所示的电路,a、b、c、d为接线柱。当合上开关K后发现灯L1和L2都不亮。经分析,其原因只可能是灯L1或L2的灯丝断
- He has lost his b____________ in the God.
- 下列关于单倍体的叙述不正确的是 ( )



