高中 数学
过 的直线
的直线 被圆
被圆 截得的线段长为2时,直线
截得的线段长为2时,直线 的斜率为( )
的斜率为( )
 的直线
的直线 被圆
被圆 截得的线段长为2时,直线
截得的线段长为2时,直线 的斜率为( )
的斜率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数f(x)是定义在R上的偶函数,且f(2)=﹣1,对任意x∈R,有f(x)=﹣f(2﹣x)成立,则f(2016)的值为( )
A . 1
B . ﹣1
C . 0
D . 2
若sin(π+α)=  ,α是第三象限的角,则
,α是第三象限的角,则  =( )
=( )
 ,α是第三象限的角,则
,α是第三象限的角,则  =( )
=( )
A .  B .
B .  C . 2
D . ﹣2
C . 2
D . ﹣2
 B .
B .  C . 2
D . ﹣2
C . 2
D . ﹣2
PA垂直于正方形ABCD所在平面,连接PB,PC,PD,AC,BD,则下列垂直关系正确的是( )
①面PAB⊥面PBC
②面PAB⊥面PAD
③面PAB⊥面PCD
④面PAB⊥面PAC.

A . ①②
B . ①③
C . ②③
D . ②④
知函数y=  的定义域为( )
的定义域为( )
 的定义域为( )
的定义域为( )
A . (﹣∞,1]
B . (﹣∞,2]
C . (﹣∞,﹣  )∩(﹣
)∩(﹣  ,1]
D . (﹣∞,﹣
,1]
D . (﹣∞,﹣  )∪(﹣
)∪(﹣  ,1]
,1]
 )∩(﹣
)∩(﹣  ,1]
D . (﹣∞,﹣
,1]
D . (﹣∞,﹣  )∪(﹣
)∪(﹣  ,1]
,1]
求下列函数的定义域.
-
(1) y=
 +
+  ;
;
-
(2) y=
 .
.
 =( )
=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  为常数,且
为常数,且  )有极大值
)有极大值 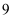 .
.
 为常数,且
为常数,且  )有极大值
)有极大值 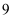 .
.
-
(1) 求
 的值;
的值;
-
(2) 若斜率为
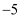 的直线
的直线  是曲线的切线,求此直线的方程.
是曲线的切线,求此直线的方程.
在  中,已知
中,已知  ,且
,且 

 ,则
,则  的轨迹方程是( )
的轨迹方程是( )
 中,已知
中,已知  ,且
,且 

 ,则
,则  的轨迹方程是( )
的轨迹方程是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若双曲线的一条渐近线方程为y=  x,则其离心率为.
x,则其离心率为.
 x,则其离心率为.
x,则其离心率为.
如图,在四棱锥 中,PA⊥底面ABCD,底面ABCD为菱形,
中,PA⊥底面ABCD,底面ABCD为菱形, ,
,  ,
,  , 点E、F分别为棱PD、AB的中点.
, 点E、F分别为棱PD、AB的中点.
 中,PA⊥底面ABCD,底面ABCD为菱形,
中,PA⊥底面ABCD,底面ABCD为菱形, ,
,  ,
,  , 点E、F分别为棱PD、AB的中点.
, 点E、F分别为棱PD、AB的中点.
-
(1) 证明:AE//平面PCF;
-
(2) 求三棱锥
 的体积.
的体积.
定义在 上的函数
上的函数 (
( 且
且 )为奇函数.
)为奇函数.
 上的函数
上的函数 (
( 且
且 )为奇函数.
)为奇函数.
-
(1) 求实数
 的值;
的值;
-
(2) 若函数
 的图象经过点
的图象经过点 , 求使方程
, 求使方程 在
在 有解的实数
有解的实数 的取值范围;
的取值范围;
-
(3) 不等式
 对于任意的
对于任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设函数![]() ,
,![]() (
(![]() ).
).
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
(参考数据:![]() ,
,![]() )
)
设![]() 是两条直线,
是两条直线, ![]() ,
, ![]() 表示两个平面,如果
表示两个平面,如果![]() ,
, ![]() ,那么“
,那么“![]() ”是“
”是“![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
设f(x)=![]() 则
则 =________.
=________.
已知函数 ,则
,则![]() 的值为( )
的值为( )
A.![]()
![]() B.
B.![]() C.15 D.
C.15 D.![]()
已知函数 ![]() 是在定义域
是在定义域 ![]() 上的偶函数,且在区间
上的偶函数,且在区间 ![]() 单调递增,若实数
单调递增,若实数 ![]() 满足
满足 ![]() ,则
,则 ![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知向量![]() ,
,![]() ,函数
,函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)在![]() 中,角
中,角![]() 对边分别是
对边分别是![]() ,且满足
,且满足![]() ,求
,求![]() 的取值范围。
的取值范围。
已知集合M={x|﹣4≤x≤7},N={x|x2![]() ﹣x﹣6>0},则M∩N为( )
﹣x﹣6>0},则M∩N为( )
A.{x|﹣4≤x<﹣2或3<x≤7} B.{x|﹣4<x≤﹣2或3≤x<7}
C.{x|x≤﹣2或x>3} D.{x|x<﹣2或x≥3}
若点![]() ,在
,在![]() 中按均匀分布出现. (1)点
中按均匀分布出现. (1)点![]() 横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点
横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点![]() 落在上述区域的概率?
落在上述区域的概率?
(2)试求方程![]() 有两个实数根的概率.
有两个实数根的概率.
最近更新
- 下列关于有关组成生物体化学元素的论述,正确的是()A. 组成生物体和组成无机自然界的化学元素中,碳元素的含量最多 B.
- 下列各句中,没有语病的一句是 ( ) A. 乳制品生产企业对在2008年9月14日以前生产的或未经批次检验三聚氰胺的乳制
- 磁共振技术可应用于临床疾病诊断。因为许多疾病会导致组织和器官内的水分发生变化,这种变化恰好能在磁共振图象中反映出来。下列
- 《庄子•齐物论》提出‘是非莫辩’的思想。庄子说:“我和你辩论,你胜了我,我果真就错了吗?我胜了你,你果真就错了吗?究竟谁
- 辛亥革命后,随着民主平等思想的进一步传播,愚昧落后的社会习俗逐渐得到改变。下列体现这一改变的是( ) A.称“老爷”
- 设为锐角,若,则的值为______
- 请用化学用语填空: (1)金刚石 (2)过氧化氢分子 (3)
- 下列关于深圳的说法正确的是A.深圳一年中正午太阳高度和昼长都有两次最大(小)值B.深圳正午太阳高度最大值和昼长最大值都出
- 政党政治是社会民主进步的重要体现。英国政党政治开始形成于 A.内战期间
- 用钠熔法可定性确定有机物中是否存在氯、溴、硫、氮等元素。下列有关有机物与足量钠反应,各元素的转化结果正确的是 A.碳元素
- 下列有关某些实验的说法中,正确的是A.在测定空气里氧气含量时,能观察到产生大量白色气体 B.在探究氢氧化钠能否与稀
- 家庭日常生活中经常用到的下列物质中,属于纯净物的是( ) A、降温用的冰水共存物
- 长江干流和黄河干流共同流经的地形区是( ) A、黄土高原 B、云贵高原 C、内蒙古高
- 阅读下面的文字,完成下面题目: 轻 点 关 门 石 文 ①费了九牛二虎之力,我们终于搬进了新居。送走了最后一批前来祝贺的
- (1)火箭推进器中盛有强还原剂液态肼(N2H4)和强氧化剂液态双氧水,当它们混合反应时,即产生大量氮气和水蒸气,并放出大
- Much he has a good taste, he can’t avoid being influen
- 右图表示某植物细胞内的代谢过程,下列有关叙述正确的是 A.X、Y物质分
- 下列哪项不是发酵过程中要完成的( ) A.随时取样检测培养液中的细菌数目、产物浓度 B.不断添加菌种 C.
- 能够用来鉴别BaCl2 、 NaCl 、Na2CO3 三种物质的试剂是 ( ) A.AgNO3溶液
- 实用类文本阅读 反思华为 ①爱反思的任正非在2000年不再在企业里提狼性,跟李一男的出走不无相关,甚至可以说正是李一男的



