高中 数学
函数f(x)=  的定义域是.
的定义域是.
 的定义域是.
的定义域是.
若复数 , 则z在复平面内对应的点位于 ( )
, 则z在复平面内对应的点位于 ( )
 , 则z在复平面内对应的点位于 ( )
, 则z在复平面内对应的点位于 ( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
已知椭圆  的离心率为
的离心率为  ,其左顶点A在圆x2+y2=12上.
,其左顶点A在圆x2+y2=12上.
 的离心率为
的离心率为  ,其左顶点A在圆x2+y2=12上.
,其左顶点A在圆x2+y2=12上.(Ⅰ)求椭圆C的方程;
(Ⅱ)直线l:x=my+3(m≠0)交椭圆C于M,N两点.
(i)若以弦MN为直径的圆过坐标原点O,求实数m的值;
(ii)设点N关于x轴的对称点为N1(点N1与点M不重合),且直线N1M与x轴交于点P,试问△PMN的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
把一颗骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组  .
.
 .
.
-
(1) 求方程组只有一个解的概率;
-
(2) 若方程组每个解对应平面直角坐标系中点P(x,y),求点P落在第四象限的概率.
若二项式  的展开式中
的展开式中  的系数为
的系数为  ,
,  的值为( )
的值为( )
 的展开式中
的展开式中  的系数为
的系数为  ,
,  的值为( )
的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知△ABC中,角A、B、C所对的边分别为a,b,c,且  =
= 
 =
= 
-
(1) 求A
-
(2) 求cosB+cosC的取值范围.
函数y=  的单调增区间是( )
的单调增区间是( )
 的单调增区间是( )
的单调增区间是( )
A .  B .
B .  C .
C .  D .
D . 
设函数 

-
(1) 若“
 ”是假命题,求实数a的取值范围;
”是假命题,求实数a的取值范围;
-
(2)
 恒成立,求实数a的取值范固
恒成立,求实数a的取值范固
已知 =(2,3),
=(2,3), =(x,-6),若
=(x,-6),若 ∥
∥ , 则x等于
, 则x等于
 =(2,3),
=(2,3), =(x,-6),若
=(x,-6),若 ∥
∥ , 则x等于
, 则x等于
A . 9
B . 4
C . -4
D . -9
过点P(2,0)的直线交抛物线y2=4x于A,B两点,若抛物线的焦点为F,则△ABF面积的最小值为.
已知  ,
,  ,
,  ,
,  ,
,  ,则下列不等式成立的是( )
,则下列不等式成立的是( )
 ,
,  ,
,  ,
,  ,
,  ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A .  B .
B .  C .
C .  D .
D . 
已知 , 且
, 且 , 则下列不等式中,正确的是 ( )
, 则下列不等式中,正确的是 ( )
 , 且
, 且 , 则下列不等式中,正确的是 ( )
, 则下列不等式中,正确的是 ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图是某几何体的三视图,则该几何体的体积是( )

A .  B .
B . 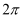 C .
C .  D .
D . 
 B .
B . 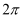 C .
C .  D .
D . 
四面体  中,若
中,若  ,则点
,则点  在平面
在平面  内的射影点
内的射影点  是
是  的( )
的( )
 中,若
中,若  ,则点
,则点  在平面
在平面  内的射影点
内的射影点  是
是  的( )
的( )
A . 外心
B . 内心
C . 垂心
D . 重心
已知X为随机变量,则下列说法错误的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
已知方程 



已知数列![]() 中,
中,![]() ,且
,且![]() 对任意正整数都成立,数列
对任意正整数都成立,数列![]() 的前
的前![]() 项和为
项和为![]()
(1) 若![]() ,且
,且![]()
(2) 是否存在实数![]() ,使数列
,使数列![]() 是公比不为1的等比数列,且对任意相邻三项
是公比不为1的等比数列,且对任意相邻三项![]() 按某顺序排列后成等差数列?若存在,求出所有的k值;若不存在,请说明理由;
按某顺序排列后成等差数列?若存在,求出所有的k值;若不存在,请说明理由;
(3) 若![]() ,求
,求![]()
设函数![]()
![]() .
.
(1)求函数![]() 的值域和零点;
的值域和零点;
(2)请判断函数![]() 的奇偶性和单调性,并给予证明.
的奇偶性和单调性,并给予证明.
在等比数列{an}中,已知a2=2,a8=32,则a5的值为 .
已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,证明:
时,证明: ![]() (其中e为自然对数的底数).
(其中e为自然对数的底数).
最近更新
- ______ Icouldn’t fully understand what he wanted to show in
- 鉴别氧气、二氧化碳两瓶气体,不可行的方法是 A.将带火星的木条分别伸入集气瓶中 B.观察两种气体的颜
- 下列词语中加点的字,每对读音都不相同的一组是( ) A. 萝卜 / 占卜 骠勇 / 骠骑 蚌埠 / 鹬蚌相争
- 在物理学的发展过程中,许多物理学家的科学发现推动了人类历史的进步。在对以下几位物理学家所作科学贡献的叙述中,正确的说法是
- 关于离子键的叙述一定正确的是( )A.离子键是通过阴、阳离子的静电吸引形成的B.金属与非金属化合,不一定都能形成离
- 1930年6月,中共中央制定了以夺取武汉为中心的全国中心城市起义及红军攻打中心城市的计划,并发出了“会师武汉,饮马长江”
- DNA分子经过诱变,某位点上一个正常碱基(设为P)变成了尿嘧啶。该DNA连续复制两次,得到4个子代DNA分子相应位点上的
- 若则是的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条
- - to many people’s expectation, the 2009 UN Climate Ch
- 31.柏杨在总结某家思想时说:“为什么在街上杀一个人是犯罪,而在战场上杀一万人是英雄?……为什么人民要忍饥挨饿去供养统治
- 曾提笔道:“山高路远坑深,大军纵横驰奔。谁敢横刀立马,唯我彭大将军!”抗日战争期间,在“彭大将军”的指挥下,中国军队主动
- 小明照镜子时看到对面墙上挂的电子表在镜子里显示的时间是实是 。
- 人体每天均需要从食物中获取各种营养物质。下列不属于人体能消化吸收的营养素是( ) A.糖类、油脂 B.蛋
- 2009年12月,在哥本哈根世界气候大会上,中国政府呼吁参会各方凝聚共识,加强合作,共同推进应对气候变化的历史进程。这表
- 子曰:“学而时习之,不亦乐乎?”但“独学而无友,则孤陋而寡闻”(《礼记·学记》),因此,“有朋自远方来,不亦乐乎”。上述
- 1894年6月孙中山《上李鸿章书》说:“试观日本一国,与西人通商后于我,仿效西方亦后于我,其维新之政为日几何,而今日成效
- 下列四组中,都属于将煤炭直接运出山西省的铁路干线是( )A.大秦线、京原线、石太线、太焦线、京九线 B.大秦线、陇
- 0.5L 1mol/L FeCl3溶液与0.2L1mol/L KCl溶液中的Cl-的浓度之比A.5 :2
- 现有四种元素的基态原子的电子排布式如下:①1s22s22p63s23p4;②1s22s22p63s23p3;③1s22s
- 《中共中央关于全面推进依法治国若干重大问题的决定》指出:必须坚持党领导立法,保证执法,支持司法,带头守法,把依法治国基本



