高中 数学
随着中国经济的迅速发展,市场石料需求急增.西部某县有丰富的优质石料,当地政府决定有序开发本县石料资源.因建立石料厂会破坏生态,该县决定石料开发走“开发治理结合,人类生态友好”的路线.当地政府请国家环保机构每年对该县与石料开发相关的生态(以下简称生态)进行评估.若生态开始变差,则下一年石料厂将停产(本问题中,时间以整数年为单位),生态友好后复产.该县在建石料厂之初投入巨资进行与之有关的生态建设,考虑到可持续发展,这种生态投入(以下简称生态投入)将逐年减少 (a是常数,
(a是常数, )亿元.该县从2021年起,若某年生态友好,则下一年生态变差的概率是
)亿元.该县从2021年起,若某年生态友好,则下一年生态变差的概率是 ;若某年生态变差,则下一年生态友好的概率为
;若某年生态变差,则下一年生态友好的概率为 . 模型显示,生态变差的概率不大于0.16683时,该县生态将不再变差,生态投入结束.
. 模型显示,生态变差的概率不大于0.16683时,该县生态将不再变差,生态投入结束.
 (a是常数,
(a是常数, )亿元.该县从2021年起,若某年生态友好,则下一年生态变差的概率是
)亿元.该县从2021年起,若某年生态友好,则下一年生态变差的概率是 ;若某年生态变差,则下一年生态友好的概率为
;若某年生态变差,则下一年生态友好的概率为 . 模型显示,生态变差的概率不大于0.16683时,该县生态将不再变差,生态投入结束.
. 模型显示,生态变差的概率不大于0.16683时,该县生态将不再变差,生态投入结束.
-
(1) 若2021年该县生态变差的概率为
 , 求该县2022年生态友好的概率;
, 求该县2022年生态友好的概率;
-
(2) 若2021年该县生态变差概率为
 , 生态投入是40亿元,a为何值时,从2021年开始到生态投入结束,对该县总生态投入额最小?并求出其最小值.
, 生态投入是40亿元,a为何值时,从2021年开始到生态投入结束,对该县总生态投入额最小?并求出其最小值.
一个人骑车以6米/秒的速度匀速追赶停在交通信号灯前的汽车,当他离汽车25米时,交通信号灯由红变绿,汽车开始做变速直线行驶(汽车与人的前进方向相同),若汽车在时刻t的速度v(t)=t米/秒,那么此人( )
A . 可在7秒内追上汽车
B . 不能追上汽车,但其间最近距离为16米
C . 不能追上汽车,但其间最近距离为14米
D . 不能追上汽车,但其间最近距离为7米
已知向量  ,
,  ,
,  .
.
 ,
,  ,
,  .
.
-
(1) 若
 ,求实数
,求实数  ,
,  的值;
的值;
-
(2) 若
 ,求
,求  与
与  的夹角
的夹角  的余弦值.
的余弦值.
已知直线  ,则过圆
,则过圆  的圆心且与直线
的圆心且与直线  垂直的直线
垂直的直线  的方程为.
的方程为.
 ,则过圆
,则过圆  的圆心且与直线
的圆心且与直线  垂直的直线
垂直的直线  的方程为.
的方程为.
已知椭圆 的离心率与等轴双曲线的离心率互为倒数关系,直线
的离心率与等轴双曲线的离心率互为倒数关系,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
 的离心率与等轴双曲线的离心率互为倒数关系,直线
的离心率与等轴双曲线的离心率互为倒数关系,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
-
(1) 求椭圆
 的方程;
的方程;
-
(2) 设
 是椭圆的上顶点,过点
是椭圆的上顶点,过点 分别作直线
分别作直线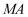 ,
,  交椭圆于
交椭圆于 ,
,  两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
,  , 且
, 且 , 求证:直线
, 求证:直线 过定点.
过定点.
在单位圆中,已知角 的终边与单位圆交于点
的终边与单位圆交于点 , 现将角
, 现将角 的终边按逆时针方向旋转
的终边按逆时针方向旋转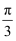 , 记此时角
, 记此时角 的终边与单位圆交于点
的终边与单位圆交于点 , 则点
, 则点 的坐标为( )
的坐标为( )
 的终边与单位圆交于点
的终边与单位圆交于点 , 现将角
, 现将角 的终边按逆时针方向旋转
的终边按逆时针方向旋转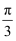 , 记此时角
, 记此时角 的终边与单位圆交于点
的终边与单位圆交于点 , 则点
, 则点 的坐标为( )
的坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知命题  ,
,  ,命题
,命题  ,使得
,使得  .若“
.若“  或
或  为真”,“
为真”,“  且
且  为假”,求实数
为假”,求实数  的取值范围.
的取值范围.
 ,
,  ,命题
,命题  ,使得
,使得  .若“
.若“  或
或  为真”,“
为真”,“  且
且  为假”,求实数
为假”,求实数  的取值范围.
的取值范围.
设曲线  在
在  处的切线为
处的切线为  ,则实数
,则实数  ( )
( )
 在
在  处的切线为
处的切线为  ,则实数
,则实数  ( )
( )
A .  B . .2
C . 1
D .
B . .2
C . 1
D . 
 B . .2
C . 1
D .
B . .2
C . 1
D . 
若(1+2x)2015=a0+a1x+a2x2+a3x3+…+a2015x2015(x∈R),则﹣  的值为( )
的值为( )
 的值为( )
的值为( )
A . ﹣2
B . ﹣1
C . 1
D . 2
设各项均为正数的数列{an}满足  =pn+r(p,r为常数),其中Sn为数列{an}的前n项和.
=pn+r(p,r为常数),其中Sn为数列{an}的前n项和.
 =pn+r(p,r为常数),其中Sn为数列{an}的前n项和.
=pn+r(p,r为常数),其中Sn为数列{an}的前n项和.
-
(1) 若p=1,r=0,求证:{an}是等差数列;
-
(2) 若p=
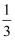 ,a1=2,求数列{an}的通项公式;
,a1=2,求数列{an}的通项公式;
-
(3) 若a2015=2015a1 , 求p•r的值.
某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠.
某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款是( )
A . 413.7元
B . 513.7元
C . 546.6元
D . 548.7元
点  的直线中,被圆
的直线中,被圆  截得的最长弦所在的直线方程为( )
截得的最长弦所在的直线方程为( )
 的直线中,被圆
的直线中,被圆  截得的最长弦所在的直线方程为( )
截得的最长弦所在的直线方程为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设函数f(x)=lnx﹣ax2+ax,a为正实数.
-
(1) 当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
-
(2) 求证:f(
 )≤0;
)≤0;
-
(3) 若函数f(x)有且只有1个零点,求a的值.
一个盒子中装有标号为1,2,3,4的4张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:
-
(1) 标签的选取是无放回的;
-
(2) 标签的选取是有放回的.
若复数  为纯虚数,则
为纯虚数,则  ( )
( )
 为纯虚数,则
为纯虚数,则  ( )
( )
A . 2
B . 1
C . -1
D . -2
如图,在三棱锥P–ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(Ⅰ)求证:PA⊥BD;
(Ⅱ)求证:平面BDE⊥平面PAC;
(Ⅲ)当PA∥平面BDE时,求三棱锥E–BCD的体积.
证明“在△ABC中至多有一个直角或钝角”,第一步应假设( )
A.三角形中至少有一个直角或钝角
B.三角形中至少有两个直角或钝角
C.三角形中没有直角或钝角
D.三角形中三个角都是直角或钝角
一个算法的程序框图如图所示,若该程序输出的结果为![]() ,则判断框内应填入的条件是
,则判断框内应填入的条件是

已知![]() 为实数,条件p:
为实数,条件p:![]() 2<
2<![]() ,条件q:
,条件q:![]() ≥1,则p是q的( )
≥1,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
函数![]() ,则
,则![]() 在
在![]() 的最大值
的最大值![]() ( )
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
最近更新
- 汉武帝统治时期,全国划分为十二个州部,每州部设刺史一名。当时刺史的主要职责是 A.监察地方政治 B.管理地方行政
- 党的十七大报告指出:提高自主创新能力,建设创新型国家,是国家发展战略的核心,是提高综合国力的关键。这说明 A.主要矛盾在
- (2011广东东莞,16,7分)某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送三”促销活动,若整箱购买,则
- 设甲、乙、丙三台机器是否需要照顾相互之间没有影响.已知在某一小时内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的
- 以石墨棒为电极分别电解以下物质,请写出电解反应的化学方程式和离子方程式。(1)Cu(NO3)2溶液;AgNO3溶液(2)
- 下列选项中不能称之为规律的是( ) ①生产关系要适应生产力 ②苹果落地 ③新陈代谢 ④水往低处流 A.②④ B
- 4.下列句子中,没有语病的一句是( ) A.美国民众在纽约发起了“占领华尔街”示威活动,抗议政府的权钱交易和贫富差距日
- All foreign visitors are requested to _____ with the regula
- 如图,直三棱柱ABC﹣A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC
- 假设地球是一半径为R、质量分布均匀的球体。一矿井深度为h,已知质量分布均匀的球壳对壳内物体的引力为零。矿井底部和地面处的
- 建立宏观与微观的联系是化学独特的思维方式。对于宏观现象的微观解释中错误的是( ) A.变瘪的乒乓球
- 已知地球上海洋面积约为316000000,把316000000用科学记数法可表示为( ) A.3.16×106
- 下列命题中为真命题的是( ) A.命题“若,则”的逆命题 B.命题“若,则”的否命题 C.命题“若,则”的否命
- “十二五”医改规划的要求,国家财政投入医改5个方面。2015年将实现统筹区域内和省内医疗费用异地即时结算。这表明财政
- 用“>”、“<”、“=”号填空 ;
- 从海水中可以提取溴,主要反应为2Br-+Cl2====2Cl-+Br2,下列说法正确的是 A.溴离子具有氧化性
- 科学家研制出一种能够选择性吸附捕获CO2的新材料。下列说法正确的是( ) A.该材料对各种气体都有很强的吸附性
- 张高水杏成熟早,上市早,史有“小满三日杏发黄”之说。果农在果园放养蜜蜂后水杏结果率明显提高,这是因为蜜蜂能促进() A.
- ——I must apologize for _______ ahead of time.——That's all ri
- 下列实验操作或记录正确的是( ) A. 用10mL量筒量取了8.65mL的水 B. 把氯化钠固体



