高中 数学
已知函数f(x)=lg(1+x)+lg(1-x).
-
(1) 求函数f(x)的定义域;
-
(2) 判断函数f(x)的奇偶性,并说明理由.
 中,内角A,B,C的对边分别为a,b,C.已知
中,内角A,B,C的对边分别为a,b,C.已知  .
.
-
(1) 求证:
 ;
;
-
(2) 若
 ,
,  的面积为
的面积为  ,求
,求  的周长.
的周长.
已知△ABC中,内角A,B,C的对边分别为a,b,c,若 =(b+a,﹣c),
=(b+a,﹣c), =(b﹣a,a+c),且
=(b﹣a,a+c),且

 ;
;
 =(b+a,﹣c),
=(b+a,﹣c), =(b﹣a,a+c),且
=(b﹣a,a+c),且

 ;
;(1)求角B的值;
(2)若a=6,b=6 , 求△ABC的面积.
, 求△ABC的面积.
已知全集为R , 设集合A={x|(x+2)(x-5)≤0},  ,C={x|a+1≤x≤2a-1}.
,C={x|a+1≤x≤2a-1}.
 ,C={x|a+1≤x≤2a-1}.
,C={x|a+1≤x≤2a-1}.
-
(1) 求A∩B , (CRA)∪B;
-
(2) 若C⊆(A∩B),求实数a的取值范围.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
(I)求证:BM∥平面ADEF;
(Ⅱ)求证:平面BDE⊥平面BEC.

已知椭圆  右焦点为F
右焦点为F  过点F的直线交E于A,B两点,若AB的中点坐标为
过点F的直线交E于A,B两点,若AB的中点坐标为  ,则E的离心率是( )
,则E的离心率是( )
 右焦点为F
右焦点为F  过点F的直线交E于A,B两点,若AB的中点坐标为
过点F的直线交E于A,B两点,若AB的中点坐标为  ,则E的离心率是( )
,则E的离心率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在△ABC中,  ,点D在线段AC上,且
,点D在线段AC上,且  ,
,
 ,点D在线段AC上,且
,点D在线段AC上,且  ,
, 
-
(1) 求
 ;
;
-
(2) 求BC和AC的长
指出下列复合命题的形式及其构成
(1)24是12和6的倍数;
(2)方程x2﹣5=0没有实根;
(3)李强是班长或杨柳是学习委员.
将分针拨快10分钟,则分针转过的弧度数是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设函数  .
.
 .
.
-
(1) 求函数
 的极值点;
的极值点;
-
(2) 设函数
 有两个零点,求整数
有两个零点,求整数  的最小值.
的最小值.
设抛物线  的焦点为F,点
的焦点为F,点  ,过
,过  的直线交C于M,N两点.当直线MD垂直于x轴时,
的直线交C于M,N两点.当直线MD垂直于x轴时,  .
.
 的焦点为F,点
的焦点为F,点  ,过
,过  的直线交C于M,N两点.当直线MD垂直于x轴时,
的直线交C于M,N两点.当直线MD垂直于x轴时,  .
.
-
(1) 求C的方程:
-
(2) 设直线
 与C的另一个交点分别为A,B,记直线
与C的另一个交点分别为A,B,记直线  的倾斜角分别为
的倾斜角分别为  .当
.当  取得最大值时,求直线AB的方程.
取得最大值时,求直线AB的方程.
在  中,
中,  ,
, 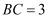 ,
,  ,
,  为
为  边上的高,
边上的高,  为
为  的中点,若
的中点,若  ,其中
,其中  ,
,  ,则
,则  等于.
等于.
 中,
中,  ,
, 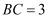 ,
,  ,
,  为
为  边上的高,
边上的高,  为
为  的中点,若
的中点,若  ,其中
,其中  ,
,  ,则
,则  等于.
等于.
双曲线的虚轴长为4,离心率  ,
,  ,
,  分别是它的左右焦点,若过
分别是它的左右焦点,若过  的直线与双曲线的左支交与A,B两点,且
的直线与双曲线的左支交与A,B两点,且  是
是  ,
,  的等差中项,则
的等差中项,则  等于( )
等于( )
 ,
,  ,
,  分别是它的左右焦点,若过
分别是它的左右焦点,若过  的直线与双曲线的左支交与A,B两点,且
的直线与双曲线的左支交与A,B两点,且  是
是  ,
,  的等差中项,则
的等差中项,则  等于( )
等于( )
A .  B .
B . 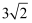 C .
C .  D . 3
D . 3
 B .
B . 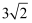 C .
C .  D . 3
D . 3
设  是公比为
是公比为  的无穷等比数列,若
的无穷等比数列,若  的前四项之和等于第五项起以后所有项之和,则数列
的前四项之和等于第五项起以后所有项之和,则数列  是( )
是( )
 是公比为
是公比为  的无穷等比数列,若
的无穷等比数列,若  的前四项之和等于第五项起以后所有项之和,则数列
的前四项之和等于第五项起以后所有项之和,则数列  是( )
是( )
A . 公比为  的等比数列
B . 公比为
的等比数列
B . 公比为  的等比数列
C . 公比为
的等比数列
C . 公比为  或
或  的等比数列
D . 公比为
的等比数列
D . 公比为  或
或  的等比数列
的等比数列
 的等比数列
B . 公比为
的等比数列
B . 公比为  的等比数列
C . 公比为
的等比数列
C . 公比为  或
或  的等比数列
D . 公比为
的等比数列
D . 公比为  或
或  的等比数列
的等比数列
已知 ,
,  , 则
, 则 的最小值是.
的最小值是.
 ,
,  , 则
, 则 的最小值是.
的最小值是.
将3封不同的信投到4个不同的邮箱,则不同的投法种数为( )
A.7 B.12
C.81 D.64
有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
(1)为了调查评委对7位歌手的支持情况,现用分层抽样方法从各组中抽取若干评委,其中从B组抽取6人,请将其余各组抽取的人数填入下表;
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 |
| 6 |
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
下列说法错误的是( )
A.一个算法应包含有限的操作步骤,而不能是无限的
B.有的算法执行完后,可能有无数个结果
C.一个算法可以有0个或多个输入
D.算法中的每一步骤都是确定的,算法的含义是唯一的
已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]()
![]() 解析式;
解析式;
(2)求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
如图所示,三棱锥 中,平面
中,平面 平面
平面 ,平面
,平面 平面
平面 ,
, 分别是
分别是 和
和 边上的点,且
边上的点,且 ,
, ,
, ,
, ,
, ,
, ,
, 为
为 的中点.
的中点.

(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.

(1)求证:
(2)求直线
最近更新
- 1. 许多物理单位常以科学家的名字命名,以科学家欧姆的名字作单位的物理量是 ( )A.电压 B
- 课文填空(共10空, 满分5分) 和其他危险相比较而言, 人类遭受鲨鱼攻击的几率其实是很小的. The chance o
- (2010·四川理综)如图所示,圆弧虚线表示正点电荷电场的等势面,相邻两等势面间的电势差相等.光滑绝缘直杆沿电场方向水
- Lucy is believed to have been killed by a vampire. She was
- 一元二次方程x2=x的解是A.x=0B.x=1C.x1=0,x2=1D.x=±1
- 西北地区是我国面积辽阔、资源丰富的地区,读图1回答下列问题.(1)A山脉是________ ;B高原是________;
- 有人说美国在破坏这次中国革命中所扮演 的角色是:“……同英国一道悍然炮击南京,给 蒋介石以沉重的压力,加快了中国大地主、
- The weather turned out to be fine yesterday. I_____ the tro
- Here is the Nine O‘clock News: 1. President Absul Krim of S
- 日常使用的金属材料,大多数属于合金。黄铜是以锌作主要添加元素的铜合金。 (1)赤铜(Cu2O)是我国古代制取黄铜的一种原
- 已知AUG、GUG为起始密码子,UAA、UGA、UAG为终止密码子。某原核生物的一个DNA片段的模板链碱基排列顺序如下:
- 下面说法中正确的是A.电磁波在任何介质中的传播速度均为3.00×108m/sB.均匀变化的电场将产生稳定的磁场,均匀变化
- 在平面直角坐标系中,设直线与圆交于两点,为坐标原点,若圆上一点满足,则 .
- 下列四种物质中,属于化合物的是() A.河水 B.冰水混合物 C .自来水 D.液氧
- 近年来,巴西农业突飞猛进,已成为全世界最大的牛肉、家禽、大豆、糖、咖啡和橙汁出口国。读巴西农业地域类型分布图,回答1~2
- 除去乙烷中少量乙烯的最好方法是( ) A.催化加氢
- (08揭阳市一模)下列有关实验操作错误的是(C) A、用药匙取用粉末状或小颗粒状固体 B、用胶头滴管滴加少量液体
- 长为5m的竖直杆下端距离一竖直隧道口为5m,若这个隧道长也为5m,让这根杆自由下落,它通过隧道的时间为
- ·启蒙运动被誉为是文艺复兴的超越与发展。其“超越与发展”的主要表现不包括 A·以理性主义为核心 B.矛头直
- 下列图像能正确反映研究水沸腾过程温度随时间变化关系的是( )



