高中 数学
 .
.
 .
.
-
(1) 讨论函数
 的单调性;
的单调性;
-
(2) 判断并说明函数
 的零点个数.若函数
的零点个数.若函数  所有零点均在区间.
所有零点均在区间.  内,求
内,求  的最小值.
的最小值.
 则g
则g  =.
=.
 ,
,  , 满足
, 满足 =(1,
=(1, ),|
),| |=3,
|=3, ⊥(
⊥( ﹣2
﹣2 ),则|
),则| ﹣
﹣ |=( )
|=( )
①已知  ,
,  都是第一象限角,若
都是第一象限角,若  ,则
,则  ;②已知
;②已知  ,
,  是钝角
是钝角  中的两个锐角,则
中的两个锐角,则  ;③若
;③若  ,
,  ,
,  是相互不互线的平面向量,则
是相互不互线的平面向量,则  与
与  垂直;④若
垂直;④若  ,
,  是平面向量的一组基底,则
是平面向量的一组基底,则  ,
,  可作为平面向量的另一组基底.其中正确的命题是(填写所有正确命题的编号).
可作为平面向量的另一组基底.其中正确的命题是(填写所有正确命题的编号).
 ,
,  为实数,则“
为实数,则“  ”是“
”是“  ”的 条件.(在“充分不必要,必要不充分,充要,既不充分又不必要”中选一个填写)
”的 条件.(在“充分不必要,必要不充分,充要,既不充分又不必要”中选一个填写)
 中,
中,  ,
,  ,
, 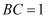 ,
,  ,
,  .
. 
-
(1) 证明:
 平面
平面  ;
;
-
(2) 若
 ,求二面角
,求二面角  的余弦值.
的余弦值.
 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
 B .
B .  C .
C .  D .
D . 
 , 现从某校随机抽取了50名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.
, 现从某校随机抽取了50名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.

-
(1) 估算该校50名学生成绩的平均值
 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
-
(2) 求这50名学生成绩在
 内的人数;
内的人数;
-
(3) 现从该校50名考生成绩在
 的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前26名的人数记为
的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前26名的人数记为
 , 求
, 求
 的分布列和数学期望.
的分布列和数学期望.
参考数据:若
 , 则
, 则
 ,
,


 中角A,B,C的对边分别为a,b,c.若
中角A,B,C的对边分别为a,b,c.若  ,则
,则  的形状为( )
的形状为( )
 , 则
, 则 ( )
( )
 B .
B .  C .
C .  D .
D . 
如图,已知椭圆![]() =1(
=1(![]() a>b>0)的离心率为
a>b>0)的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(![]() +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.

(1)求椭圆和双曲线的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1;
(3)是否存在常数λ,使得|AB|+|CD|=λ|AB|·|CD|恒成立?若存在,求λ的值;若不存在,请说明理由.
如图,用5种不同颜色给图中的A、B、C、D四个区域涂色,规定一个区域只涂一种颜色,相邻区域必须涂不同的颜色,不同的涂色方案有________种.

已知f(x+1)=![]() ,f(1)=1(x∈N*),猜想f(x)的表达式为( )
,f(1)=1(x∈N*),猜想f(x)的表达式为( )

在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,![]() ).若S1,S2,S3分别为三棱锥D
).若S1,S2,S3分别为三棱锥D![]() ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )
ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )
(A)S1=S2=S3 (B)S2=S1且S2≠S3
(C)S3=S1且S3≠S2 (D)S3=S2且S3≠S1
设a∈R,复数![]() (i为虚数单位)是纯虚数,则a的值为__________.
(i为虚数单位)是纯虚数,则a的值为__________.
设a,b,c为一个三角形的三条边,s=(a+b+c),且s2=2ab,试证:s<2a.
已知A(-1,a)、A(a,8)两点的直线与直线2x-y+1=0平行,则a的值为
A.-10 B. 2 C. 10 D.-2
- 已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为 .
- 人在遇到危险的时候,会爆发出比平时更大的力量和产生更敏捷的反应,此时如测定其体内激素水平,明显提高的是 A.胰岛素
- 划分东西半球的界线是:( ) A.0°和180°经线 B.西经20°和东经160°经线 C. 赤道
- 下图是鸟卵的结构图,请据图回答。(1)图中⑤的结构是____ ,是进行胚胎发育的部位.(2)图中的⑥是指______
- 中国古代精美的手工业品,反映出古代中国文明成就的辉煌。下列产品中,清代才出现的是 ( )①五彩镂空云凤纹瓶
- .......
- 山梨酸是一种常见的食物添加剂,它是一种无色针状晶体或白色粉末,它的结构简 式为。下列关于山梨酸的叙述不正确的是 A.山梨
- 把A、B、C、D四块金属泡在稀H2SO4中,用导线两两相连可以组成各种原电池。A、B相连时,A为负极;C、D相连时,D上
- The oceans are unique to our planet. No other planet in our
- 在“观察水的沸腾实验”中,用温度计测小烧杯中水的初温时的操作过程如图甲所示,水在沸腾时温度计示数如图乙所示。(1)图中操
- 求下列函数的导数.(1)y=x4-3x2-5x+6;(2)y=x · tanx;(3)y=(x+1)(x+2)(x+3)
- 某中学举行“走进文学百花园”语文实践活动。请你按照活动要求,凭借自身的语文素养,打开“三重门”,进入“百花园”。 ①第一
- 2012年2月新华网报道,加拿大开发出生产医用放射性同位素的简单方法。下列关于的叙述正确的是 A.原子序数是99 B.
- 根据下述材料,运用《经济生活》知识回答问题。 材料一:某村有30亩河滩地,因常发洪水被各承包农户摞荒。村委会协调将其转包
- 给出下列命题:①三条线段组成的图形叫三角形 ②三角形相邻两边组成的角叫三角形的内角 ③三角形的角平分线是射线 ④三
- --- How is the project going?--- Fairly well. We have _____
- —Please take the notebook to yoursister. —______. A. Fine,
- 用1000 t含氧化铁80%赤铁矿石,理论上可以炼出含铁96%的生铁的质量是多少
- 已知函数 (I)若函数 (II)设的充分条件,求实数m的取值范围.
- 阅读《生活中的减法》,完成1—3题。 生活中的减法 ①“人生不如意事常八九”,这不如意事,又差不多八九成是由他人给咱带来



