高中数学：高一　 高二　 高三　 高考　

高中数学

已知二面角α﹣l﹣β的大小为60°，点P在面α内，设P在平面β上的射影为Q.且PQ＝ $\text{[math]}$ ，则Q到平面α的距离为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 3

计算机执行如图的程序段后，输出的结果是（　　）

A . 1，3 B . 4，1 C . 4，﹣2 D . 1，﹣2

函数 $\text{[math]}$ 的单调递减区间是.

下列算法正确的是（）

A .

B .

C .

D .

如图，三棱锥 $\text{[math]}$ 的底面为直角三角形， $\text{[math]}$ 为斜边 $\text{[math]}$ 的中点，顶点 $\text{[math]}$ 在底面的投影为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .

（1）求 $\text{[math]}$ 的长；
（2）求二面角 $\text{[math]}$ 的余弦值.

已知命题p：∀x＞0，ln（x+1）＞0；命题q：若a＞b，则a²＞b² ，下列命题为真命题的是（　　）

A . p∧q B . p∧￢q C . ￢p∧q D . ￢p∧￢q

在区间 $\text{[math]}$ 上随机地取一个数 $\text{[math]}$ ,则 $\text{[math]}$ 的概率为.

已知函数 $\text{[math]}$ 在 $\text{[math]}$ 处取得最大值，则函数 $\text{[math]}$ 的图象（）

A . 关于点 $\text{[math]}$ 对称 B . 关于点 $\text{[math]}$ 对称 C . 关于直线 $\text{[math]}$ 对称 D . 关于直线 $\text{[math]}$ 对称

向量 $\text{[math]}$ 与 $\text{[math]}$ 的夹角为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 则 $\text{[math]}$ =（）

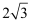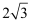A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . 12

已知数列{a_n}满足a_n＞0，a₁=2，且（n+1）a_n₊₁²=na_n²+a_n（n∈N*）．

（Ⅰ）证明：a_n＞1；

（Ⅱ）证明： $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$ ＜ $\text{[math]}$ （n≥2）．

函数y=log_a（x+4）-1（a＞0且a≠1）的图象恒过定点A，若点A在直线mx+ny+1=0上，其中m，n均大于0，则 $\text{[math]}$ 的最小值为（）

A . 2 B . 6 C . $\text{[math]}$ D . 10

已知函数 $\text{[math]}$ ， $\text{[math]}$ ．

（1）当 $\text{[math]}$ 为何值时， $\text{[math]}$ 轴为曲线 $\text{[math]}$ 的切线；
（2）用 $\text{[math]}$ 表示 $\text{[math]}$ 中的最小值，设函数 $\text{[math]}$ ，讨论 $\text{[math]}$ 零点的个数．