高中 数学
设函数  ,
,  .
.
 ,
,  .
.
-
(1) 当
 时,求函数
时,求函数  的最小值;
的最小值;
-
(2) 当
 时,求函数
时,求函数  的最小值.
的最小值.
求与直线3x-4y+7=0平行,且在两坐标轴上截距之和为1的直线l的方程.
某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计销售量从今年开始每年比上一年增加10万只,第n次投入后,每只产品的固定成本为  (k>0,k为常数,
(k>0,k为常数,  且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为  万元.
万元.
 (k>0,k为常数,
(k>0,k为常数,  且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为  万元.
万元. (Ⅰ)求k的值,并求出  的表达式;
的表达式;
(Ⅱ)若今年是第1年,问第几年年利润最高?最高利润为多少万元?
 的展开式中
的展开式中  的系数为( )
的系数为( )
A . -84
B . 84
C . -280
D . 280
已知复数  ,若
,若  是实数,则实数
是实数,则实数  的值为( )
的值为( )
 ,若
,若  是实数,则实数
是实数,则实数  的值为( )
的值为( )
A . 0
B .  C . 6
D . -6
C . 6
D . -6
 C . 6
D . -6
C . 6
D . -6
已知α,β是两个不同的平面,l,m,n是不同的直线,下列命题不正确的是( )A
A . 若l⊥m,l⊥n,m⊂α,n⊂α,则l⊥α
B . 若l∥m,l⊄α,m⊂α,则l∥α
C . 若α⊥β,α∩β=l,m⊂α,m⊥l,则m⊥β
D . 若α⊥β,m⊥α,n⊥β,则m⊥n
若复数z满足  =1,其中i为虚数单位,则复数z的模为( )
=1,其中i为虚数单位,则复数z的模为( )
 =1,其中i为虚数单位,则复数z的模为( )
=1,其中i为虚数单位,则复数z的模为( )
A . 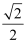 B .
B .  C . 2
C . 2  D . 4
D . 4 
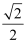 B .
B .  C . 2
C . 2  D . 4
D . 4 
一船以每小时  的速度向东航行,船在
的速度向东航行,船在  处看到一个灯塔
处看到一个灯塔  在北偏东
在北偏东  ,行驶
,行驶  后,船到达
后,船到达  处,看到这个灯塔在北偏东
处,看到这个灯塔在北偏东  ,这时船与灯塔的距离为
,这时船与灯塔的距离为 
 的速度向东航行,船在
的速度向东航行,船在  处看到一个灯塔
处看到一个灯塔  在北偏东
在北偏东  ,行驶
,行驶  后,船到达
后,船到达  处,看到这个灯塔在北偏东
处,看到这个灯塔在北偏东  ,这时船与灯塔的距离为
,这时船与灯塔的距离为 
函数  的定义域是.
的定义域是.
 的定义域是.
的定义域是.
本式  的值是( )
的值是( )
 的值是( )
的值是( )
A . 1
B . ﹣1
C .  D .
D . 
 D .
D . 
已知函数  .
.
 .
.
-
(1) 当x∈(0,1)时,求f(x)的单调性;
-
(2) 若h(x)=(x2﹣x)•f(x),且方程h(x)=m有两个不相等的实数根x1 , x2 . 求证:x1+x2>1.
若a>b>0,则( )
A .  c>
c> c(c∈R)
B .
c(c∈R)
B .  C . lg(a﹣b)>0
D .
C . lg(a﹣b)>0
D . 
 c>
c> c(c∈R)
B .
c(c∈R)
B .  C . lg(a﹣b)>0
D .
C . lg(a﹣b)>0
D . 
等差数列{an}中,a3=7,a9=19,则a5为( )
A . 13
B . 12
C . 11
D . 10
设命题  ,
,  ,则
,则  为.
为.
 ,
,  ,则
,则  为.
为.
函数 (a>0且a≠1)的图象必经过点( )
(a>0且a≠1)的图象必经过点( )
 (a>0且a≠1)的图象必经过点( )
(a>0且a≠1)的图象必经过点( )
A . (0,1)
B . (2,1)
C . (3,1)
D . (3,2)
已知函数 的值域是
的值域是 , 则实数
, 则实数 的取值范围是 ( )
的取值范围是 ( )
 的值域是
的值域是 , 则实数
, 则实数 的取值范围是 ( )
的取值范围是 ( )
A .  ;
B .
;
B .  ;
C .
;
C .  ;
D .
;
D .  .
.
 ;
B .
;
B .  ;
C .
;
C .  ;
D .
;
D .  .
.
已知函数  ,若曲线
,若曲线  在点
在点  处与直线
处与直线  相切,则
相切,则  ( )
( )
 ,若曲线
,若曲线  在点
在点  处与直线
处与直线  相切,则
相切,则  ( )
( )
A . 1
B . 0
C . -1
D . -1或1
某商超通过产品、价格、渠道和促销等各种营销策略,销售业绩得到不断提升,商超利润也有较大的攀升,经统计,该商超近7周的利润数据如下:
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
商超利润 | 32 | 35 | 36 | 45 | 47 | 51 | 55 |
附: ;参考数据:
;参考数据:
-
(1) 若
 关于
关于 具有较强的线性相关关系,求
具有较强的线性相关关系,求 关于
关于 的线性回归方程
的线性回归方程 , 并预测该商超下周的利润;
, 并预测该商超下周的利润;
-
(2) 该商超为提升业绩,决定对客户开展抽奖促销活动:单张小票不超过500元可参加抽奖一次;单张小票超过500元可参加抽奖两次.若抽中“一等奖”,可获得30元的代金券;抽中“二等奖”,可获得20元的代金券;抽中“谢谢参与”,则没有奖励.已知本次抽奖活动中获得“一等奖”的概率为
 , 获得二等奖”的概率为
, 获得二等奖”的概率为 .某客户有两次参与抽奖活动的机会,假设两次抽奖之间是否中奖相互独立,求该客户所获得代金券总额
.某客户有两次参与抽奖活动的机会,假设两次抽奖之间是否中奖相互独立,求该客户所获得代金券总额 (元)的分布列及数学期望.
(元)的分布列及数学期望.
若函数f(x)=ax2-x-1有且仅有一个负零点,求实数a的取值范围.
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重:
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
某市2012年3月8日﹣4月7日(30天)对空气质量指数PM2.5进行检测,获得数据后整理得到如图条形图:
(1)估计该城市一个月内空气质量类别为良的概率;
(2)从空气质量级别为三级和四级的数据中任取2个,求至少有一天空气质量类别为中度污染的概率.


最近更新
- 请回答下列有关水的问题: (1)自来水生产过程中常用过滤的方法除去水中不溶性杂质,再进行消毒。X是一种常见的自来水消毒剂
- 某厂家想调查该厂产品“回头客”的情况,根据随机抽样得到如下的2×2列联表: 以前采购过以前未采购合计目前采购351550
- 水平桌面上一重200 N的物体,与桌面间的动摩擦因数是0.2,当依次用15 N和80 N的水平拉力拉此物体时,物体受到的
- 若是以5为周期的奇函数,且,则 ————————————
- 有关A1型密堆积与A3型密堆积的说法中,正确的是( )A.A1型密堆积是最密堆积,A3型密堆积不是最密堆积B.两者都
- “没有人富有得可以不要别人的帮助,也没有人穷得不能在某方面给他人帮助”这话意在说明 A.人的价值在于创造价值
- 根据下面的文字,给“数学语言学”下定义。(50个字左右) 把数学和语言学这两门相距甚远的学科紧密联系起来的强有力的纽带,
- 当前,我们之所以要对青少年进行世界观、无神论教育,是因为A.世界观是人们对整个世界及人和世界关系的根本观点和总的看法
- 按要求进行句型转换。每空一词。【小题1】My computer game is in the bookcase.(对划线
- 直线与抛物线交于A、B两点,O为坐标原点,且,则 ▲
- It is notright to judge a person ______ the clothes he wear
- 下列原子或离子的电子排布式错误的是( ) A.Na+:1s22s22p6 B.O2-:1s22s22p4
- 已知直线l的倾斜角为135,且经过点P(1,1). (Ⅰ)求直线l的方程; (Ⅱ)求点A(3,4)关于直线l的对称点A
- .如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°, 则∠2的度数为() A.20
- 新航路开辟后,世界各地相对孤立的状态被打破,世界历史逐渐融合成一部统一的人类史。推动这一过程的方式有①西方掠夺与贸易 ②
- 下列各句中,没有语病的一句是( )A、正如这雄伟的高原上若没有了青海湖、纳木错、羊卓雍这一眼眼圣水的灵秀将黯然失色一样,
- 城市道路刷黑后,行车时感觉更平稳,且噪声比原来小。小明经过仔细观察后认为,这可能是沥青比水泥路面软,有 功能,同时道
- 在《资本论》一书中,对资本曾有过一段精彩的论述:“资本来到人间,从头到脚,每个毛孔都滴着血和肮脏的东西。”据此,你认为下
- 如图,小明准备撰写关于明代手工工场生产的历史小论文。他主要查阅的著作是:( )
- 如图电路,灯泡标有“12V 6W”,滑动变阻器R1标有“100Ω 1A”,电压表量程为0~15V,电流表量程为0~0



