高中 数学
已知 ,
,  .
. =0,点C满足
=0,点C满足
 +
+ (
( ),且
),且 , 则
, 则 等于( )
等于( )
 ,
,  .
. =0,点C满足
=0,点C满足
 +
+ (
( ),且
),且 , 则
, 则 等于( )
等于( )
A .  B . 1
C .
B . 1
C .  D .
D . 
 B . 1
C .
B . 1
C .  D .
D . 
已知圆 经过函数
经过函数 的图象与坐标轴的3个交点.
的图象与坐标轴的3个交点.
 经过函数
经过函数 的图象与坐标轴的3个交点.
的图象与坐标轴的3个交点.
-
(1) 求圆
 的标准方程;
的标准方程;
-
(2) 若点
 为圆
为圆 :
: 上一动点,点
上一动点,点 为圆
为圆 上一动点,点
上一动点,点 在直线
在直线 上运动,求
上运动,求 的最小值,并求此时点
的最小值,并求此时点 的横坐标.
的横坐标.
设集合  ,
,  ,则
,则  中元素的个数为( )
中元素的个数为( )
 ,
,  ,则
,则  中元素的个数为( )
中元素的个数为( )
A . 0
B . 2
C . 3
D . 4
设  ,
,  满足约束条件
满足约束条件  ,若
,若  的最大值为( )
的最大值为( )
 ,
,  满足约束条件
满足约束条件  ,若
,若  的最大值为( )
的最大值为( )
A .  B .
B .  C .
C .  D .
D . 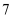
 B .
B .  C .
C .  D .
D . 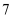
如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.

-
(1) 证明:AC1⊥A1B;
-
(2) 设直线AA1与平面BCC1B1的距离为
 ,求二面角A1﹣AB﹣C的大小.
,求二面角A1﹣AB﹣C的大小.
已知函数 .
.
 .
.
-
(1) 求函数
 的极值;
的极值;
-
(2) 求函数
 在区间
在区间 上的最值.
上的最值.
已知命题p:“  ,函数
,函数  无零点”,命题q:“方程
无零点”,命题q:“方程  有两个不相等的正实数根”,若命题p与命题q有且只有一个真命题,求实数m的取值范围.
有两个不相等的正实数根”,若命题p与命题q有且只有一个真命题,求实数m的取值范围.
 ,函数
,函数  无零点”,命题q:“方程
无零点”,命题q:“方程  有两个不相等的正实数根”,若命题p与命题q有且只有一个真命题,求实数m的取值范围.
有两个不相等的正实数根”,若命题p与命题q有且只有一个真命题,求实数m的取值范围.
如图,在三棱锥P﹣ABC中,D,E分别是BC,AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P﹣BC﹣A的平面角为γ,则α,β,γ的大小关系是( )

A . α<β<γ
B . α<γ<β
C . β<α<γ
D . γ<β<α
已知点P(x,y)在圆x2+y2﹣6x﹣6y+14=0上.
求x2+y2+2x+3的最大值与最小值.
下列函数中,满足f(2x)=2f(x)的是( )
A . f(x)=|x|
B . f(x)=x-|x|
C . f(x)=x+1
D . f(x)=-x
设2a=3,2b=6,2c=12,则数列a,b,c成 ( )
A . 等差数列
B . 等比数列
C . 非等差也非等比数列
D . 既等差也等比数列
如图,有一位于  处的台风预测站,某时刻发现其北偏东45º且与
处的台风预测站,某时刻发现其北偏东45º且与  相距
相距  海里的
海里的  处有一台风中心正以匀速直线移动,20分钟后又测得该台风中心位于预测站
处有一台风中心正以匀速直线移动,20分钟后又测得该台风中心位于预测站  北偏东
北偏东  ,且与预测站
,且与预测站  相距
相距  海里的
海里的  处.已知
处.已知  ,
,  为锐角.
为锐角.
 处的台风预测站,某时刻发现其北偏东45º且与
处的台风预测站,某时刻发现其北偏东45º且与  相距
相距  海里的
海里的  处有一台风中心正以匀速直线移动,20分钟后又测得该台风中心位于预测站
处有一台风中心正以匀速直线移动,20分钟后又测得该台风中心位于预测站  北偏东
北偏东  ,且与预测站
,且与预测站  相距
相距  海里的
海里的  处.已知
处.已知  ,
,  为锐角.
为锐角. 
-
(1) 求该台风中心移动的速度
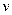 (海里/小时);
(海里/小时);
-
(2) 在离预测站
 的正南方有半径为5海里的圆形小岛,其中心
的正南方有半径为5海里的圆形小岛,其中心  距离
距离  处20海里,如果台风中心移动速度和方向均不改变,则该小岛是否会受台风影响?若小岛受影响,则受影响时间是否超过15分钟?请说明理由.
处20海里,如果台风中心移动速度和方向均不改变,则该小岛是否会受台风影响?若小岛受影响,则受影响时间是否超过15分钟?请说明理由.
已知一次考试共有60名同学参加,考生的成绩X~N(110,25).据此估计,大约应有57人的分数在区间( )
A.(90,110]内 B.(95,125]内
C.(100,120]内 D.(105,115]内
已知圆锥母线长为5,底面圆半径长为4,点![]() 是母线
是母线![]() 的中点,
的中点,![]() 是底面圆的直径,点
是底面圆的直径,点![]() 是弧
是弧![]() 的中点.
的中点.
(1)求三棱锥![]() 的体积;
的体积;
(2)求异面直线![]() 与
与![]() 所成的角.
所成的角.

用数学归纳法证明![]() +
+![]() +
+![]() +…+
+…+![]() 假设n=k时,不等式成立,则当n=k+1时,应推证的目标是( )
假设n=k时,不等式成立,则当n=k+1时,应推证的目标是( )

.抛物线 ![]() 的焦点为
的焦点为 ![]() 为抛物线上一点,若
为抛物线上一点,若 ![]() 的外接圆与抛物线的准线相切(
的外接圆与抛物线的准线相切( ![]() 为坐标原点),且外接圆的面积为
为坐标原点),且外接圆的面积为 ![]() ,则
,则 ![]() .
.
一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东![]() ,行驶4h后,船到达C处,看到这个灯塔在北偏东
,行驶4h后,船到达C处,看到这个灯塔在北偏东![]() ,这时船与灯塔的距离为多少km.( )
,这时船与灯塔的距离为多少km.( )
A.20![]() B.30
B.30![]() C.15
C.15![]() D.30
D.30![]()
计算:![]()
已知等比数列![]() 的前n项和
的前n项和![]() ,则数列
,则数列![]() 的前10项和等于( )
的前10项和等于( )
A.1023 B.55 C.45 D.35
若x,y满足约束条件 .则
.则![]() 的最大值为 .
的最大值为 .
最近更新
- 请选出下列文学常识表述不正确的一项A.《小石潭记》、《记承天寺夜游》、《巴东三峡》、《周庄水韵》都属于游记。B.《记承天
- 设f(x)是定义在R上的函数,且满足f(x+2)=f(x+1)﹣f(x),如果f(1)=lg,f(2)=lg15,则f=
- 下面叙述正确的是( ) A.元素相对原子质量的小数都因有同位素而形成的 B.有相同质子数的原子或离子一定属于同种元素
- 用最简便的方法检验生石灰水中含有未完全分解完的碳酸钙:(1)所加试剂是 ;(2)观察到的现象是
- (08年湖南六校联考文)已知,若单位向量与共线,则向量的坐标为
- 中国古代中枢权力体系的变化,突出了相权与皇权的争夺,以相权的削弱展现了古代中国专制皇权不断加强的趋势。黄宗羲曾经有这样的
- p{font-size:10.5pt;line-height:150%;margin:0;padding:0;}td{f
- 下列句句中,没有语病的一句是( ) A.近日,中国人民大学校长纪宝成在《人民日报》撰文指出,在外界现实利益的诱惑
- 下图为我国某河流简图。回答2题。上图所示区域的自然环境是 A.由于常年受副热带高压控制,气候干旱少雨 B.此河流的主要补
- B......
- 下列运算正确的是( ) A.(a2)3=a5 B.(a﹣b)2=a2﹣b2 C.2a2+a=3a3 D.
- 2008年9月23日,宁夏回族自治区成立50周年。50年来,宁夏回族自治区的经济和社会事业都取得了巨大的成绩,今后国家还
- 用某种羧酸的结晶水合物晶体A进行实验: ①6.3 g晶体在一定条件下完全分解,生成2.2 gCO2、1.4 g CO和2
- 下列作品揭示了我国封建社会走向没落历史史实的是( )A、《三国演义》 B、《水浒 》C、《西游记 》 D
- 罗马万民法规定奴隶在法律上是“可以买卖的东西”,宣称保护除奴隶之外的自由民的权利。这说明它是 A保护自由民的私有财产
- 一位英国人说,中国多织一匹布,英国就会少销一匹,因而“机器不宜进中国”。这句话反映出的本质问题是( ) A.自然经济
- 下列反应中,H 2O 做氧化剂的是A . SO 3+H 2O=H 2SO 4B . 3NO 2+H 2O=2HNO 3+
- 如图是人的耳和脑的示意图,请据图分析回答:(1)上课铃响了,同学们听到铃声后陆续走进教室。请用图中字母及箭头写出听觉形成
- 2009年是新中国成立60周年。回答下面试题。 33.新中国成立60年来,伴随着我国经济社会的发展,公民的政治参与也呈现
- 甲醇(CH3OH)有毒,误饮可使眼睛失明,甚至死亡。最新研究发现,在细菌作用下,用氨气(NH3)处理含有甲醇的工业废水,



