高中 数学
已知

(1)求 的值;
的值;
(2)当x∈(﹣t,t](其中t∈(﹣1,1),且t为常数)时,f(x)是否存在最小值,如果存在求出最小值;如果不存在,请说明理由;
(3)当f(x﹣2)+f(4﹣3x)≥0时,求满足不等式f(x﹣2)+f(4﹣3x)≥0的x的范围.
对椭圆有结论一:椭圆C: (a>b>0)的右焦点为F(c,0),过点P(
(a>b>0)的右焦点为F(c,0),过点P( , 0)的直线l交椭圆于M,N两点,点M关于x轴的对称点为M′,则直线M′N过点F.类比该结论,对双曲线有结论二,根据结论二知道:双曲线C′:
, 0)的直线l交椭圆于M,N两点,点M关于x轴的对称点为M′,则直线M′N过点F.类比该结论,对双曲线有结论二,根据结论二知道:双曲线C′: ﹣y2=1的右焦点为F,过点P(
﹣y2=1的右焦点为F,过点P( , 0)的直线与双曲线C′右支有两交点M,N,若点N的坐标是(3,
, 0)的直线与双曲线C′右支有两交点M,N,若点N的坐标是(3, ),则在直线NF与双曲线的另一个交点坐标是
),则在直线NF与双曲线的另一个交点坐标是
 (a>b>0)的右焦点为F(c,0),过点P(
(a>b>0)的右焦点为F(c,0),过点P( , 0)的直线l交椭圆于M,N两点,点M关于x轴的对称点为M′,则直线M′N过点F.类比该结论,对双曲线有结论二,根据结论二知道:双曲线C′:
, 0)的直线l交椭圆于M,N两点,点M关于x轴的对称点为M′,则直线M′N过点F.类比该结论,对双曲线有结论二,根据结论二知道:双曲线C′: ﹣y2=1的右焦点为F,过点P(
﹣y2=1的右焦点为F,过点P( , 0)的直线与双曲线C′右支有两交点M,N,若点N的坐标是(3,
, 0)的直线与双曲线C′右支有两交点M,N,若点N的坐标是(3, ),则在直线NF与双曲线的另一个交点坐标是
),则在直线NF与双曲线的另一个交点坐标是
已知函数  ,其中
,其中  .
.
 ,其中
,其中  .
.
-
(1) 当
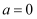 时,求
时,求  的最大值和最小值;
的最大值和最小值;
-
(2) 当
 时,证明:
时,证明:  在
在  上有且仅有一个极大值点和一个极小值点(分别记为
上有且仅有一个极大值点和一个极小值点(分别记为  ),且
),且  为定值.
为定值.
已知函数f(x)=  +b(a,b∈R)的图象在点(1,f(1))处的切线方程为y=x﹣1.
+b(a,b∈R)的图象在点(1,f(1))处的切线方程为y=x﹣1.
 +b(a,b∈R)的图象在点(1,f(1))处的切线方程为y=x﹣1.
+b(a,b∈R)的图象在点(1,f(1))处的切线方程为y=x﹣1.
-
(1) 求实数a,b的值及函数f(x)的单调区间.
-
(2) 当f(x1)=f(x2)(x1≠x2)时,比较x1+x2与2e(e为自然对数的底数)的大小.
已知数列{an}满足a1=1,  求数列(an)的通项公式为an=。
求数列(an)的通项公式为an=。
 求数列(an)的通项公式为an=。
求数列(an)的通项公式为an=。
出版商为了解某科普书一个季度的销售量y(单位:千本)和利润x(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
x |
2.4 |
3.1 |
4.6 |
5.3 |
6.4 |
7.1 |
7.8 |
8.8 |
9.5 |
10 |
|
y |
18.1 |
14.1 |
9.1 |
7.2 |
4.9 |
3.9 |
3.2 |
2.3 |
2.1 |
1.4 |

根据上述数据画出如图所示的散点图:
参考公式及参考数据:
①对于一组数据(u1 , v1),(u2 , v2),…,(un , vn),其回归直线  的斜率和截距的公式分别为
的斜率和截距的公式分别为  ,
,  .
.
②参考数据:
| | | | | | | |
| 6.50 | 6.63 | 1.75 | 82.50 | 2.70 | -143.25 | -27.54 |
表中ui=Inxi ,  =
=  .另:In4.06≈1.40.计算时,所有的小数都精确到0.01.
.另:In4.06≈1.40.计算时,所有的小数都精确到0.01.
-
(1) 根据图中所示的散点图判断y=ax+b和y=clnx+d哪个更适宜作为销售量y关于利润x的回归方程类型?(给出判断即可,不需要说明理由);
-
(2) 根据(1)中的判断结果及参考数据,求出y关于x的回归方程;
-
(3) 根据回归方程分析:设该科普书一个季度的利润总额为:(单位:千元),当季销售量y为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
设x>0,y>0,A、B、P三点共线且向量  =x
=x  +y
+y  ,则
,则  的最小值( )
的最小值( )
 =x
=x  +y
+y  ,则
,则  的最小值( )
的最小值( )
A . 4
B . 2
C . 9
D . 10
已知平行六面体  中,底面
中,底面  是边长为1的正方形,
是边长为1的正方形,  ,
,  ,则
,则  .
.  .
.
 中,底面
中,底面  是边长为1的正方形,
是边长为1的正方形,  ,
,  ,则
,则  .
.  .
.
在△ABC中,一定成立的等式是( )
A . asinA=bsinB
B . acosA=bcosB
C . asinB=bsinA
D . acosB=bcosA
某校共有高一、高二、高三学生共有1290人,其中高一480人,高二比高三多30人,为了解该校学生健康状态,现采用分层抽样方法进行调查,在抽取的样本中有高一学生96人,则该样本中的高三学生人数为( )
A . 84
B . 78
C . 81
D . 96
若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是.

设定义域为R的函数f(x)=  .
.
 .
. 
-
(1) 在如图所示的平面直角坐标系内作出函数f(x)的图象,并写出函数f(x)的单调区间(不需证明);
-
(2) 求函数f(x)在区间[1,4]上的最大值与最小值.
设随机变量 的分布列如下:
的分布列如下:
 的分布列如下:
的分布列如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
P |
|
|
|
|
|
|
|
|
|
|
且数列 满足
满足 , 则
, 则 .
.
已知函数f(x)是定义域为R上的奇函数,当x>0时,f(x)=x2+2x.
(1)求f(x)的解析式;
(2)若不等式f(t﹣2)+f(2t+1)>0成立,求实数t的取值范围.
已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知 , 且
, 且 , 若
, 若 , 且
, 且 , 则实数
, 则实数 的取值范围为.
的取值范围为.
 , 且
, 且 , 若
, 若 , 且
, 且 , 则实数
, 则实数 的取值范围为.
的取值范围为.
已知函数 , 则
, 则 ( )
( )
 , 则
, 则 ( )
( )
A . 5
B . 3
C . 2
D . -2
已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 的值是________.
的值是________.
、已知集合A={![]() },B={
},B={![]() },则A
},则A![]() B等于___________.
B等于___________.
某大学数学系共有学生5000人,其中一、二、三、四年级的人数比为4∶3∶2∶1,要用分层抽样的方法从数学系所有学生中抽取一个容量为200的样本,则应抽取三年级的学生人数为 ( )
A.80 B.40 C.60 D.20
最近更新
- 依次填入下列横线处的词语,最恰当的一组是( ) ①半个世纪以来,党的三代领导集体对南水北调工程十分关心、高度重
- 下列各句中,标点符号使用正确的一项是( ) A.她看上去十七、八岁,一幅瘦骨伶仃的样子。 B.花园里有好多花,月季
- (1)加热蒸干Al2(SO4)3(aq),得到的固体物质是______________________(写化学式)。(2
- ⑴ 下列对名著名篇的主要内容和艺术特色表述有误的两个选项是:( )( )(5分) A.“赤壁之战”是诸葛亮出山之后参与指
- 基础写作(共1小题,满分15分) 最近,你班举行了一个“What will the future be like?”的专
- 公元8世纪初,法兰克王国一位宫相在位时,开始对封建分封制度进行改革,这位宫相是 A、查理·马特 B
- (本小题满分12分)数列的前n项和为,且满足, 数列中,,且点在直线上, (1)求数列、的通项公式; (2)设, 求;(
- 已知函数(2≤x≤4),(1)求输入时对应的y值;(2)令,求y关于t的函数关系式,t的范围;(3)求该函数的值域.
- 24.纯合白色球状南瓜与纯合黄色盘状南瓜相交(两对基因独立遗传),F1全为白色盘状南瓜。若F2中有纯合的白色球状南瓜38
- 水已成为影响人类可持续发展的重要因素之一。下图为世界主要城市用水价格比较,据图判断2~3题。2.2001年我国北京等许
- 春节是中华民族阖家团圆的传统节日,正像明星王宝强所唱的那样,“有钱没钱,回家过年”。从这一国情出发,国家决定不再实行春运
- (08广州)在图12中用线代表绳子,将两个滑轮连成省力的滑轮组,要求人用力往下拉绳使重物升起
- 吸烟有害健康.为了鉴定烟雾中是否存在CO2和CO,对香烟燃烧产生的烟雾进行适当处理后,依次通过足量的以下试剂(每步都吸收
- 2010年1月19日,2009年度安徽“十大新闻”、“十大新闻人物”评选颁奖晚会“安徽力量”圆满落幕,评选结果全部揭晓。
- 酒石酸是某种降压药物的载体,可用1,3-丁二烯为原料合成,其流程如下:已知:① ② D的分子组成是C4H8O2Cl2
- 读下图,完成有关要求。 ⑴A点的经度是_________,纬度是______。⑵图中①、②、③、④四地中,位于西半球的是
- 转基因植物中的哪类基因被删除,不会影响到转基因植物的正常生理活动和人们期望其具有的功能()A.目的基因 B.显
- 已知299 K时,合成氨反应N2(g)+ 3H2 (g) 2NH3(g) △H = -92.0 kJ/mol,将此温度
- —Could you turn the TV down a little bit? —______. Is it
- 将加横线的长句改为整散结合的短句。 柿叶一落,槐叶一飘,京华的秋树便相继凋落了;落叶在公园里和马路上稠密如雨萧萧地下。