高中 数学
已知函数  ,若单调递增数列
,若单调递增数列  满足
满足  ,则实数
,则实数  的取值范围为.
的取值范围为.
 ,若单调递增数列
,若单调递增数列  满足
满足  ,则实数
,则实数  的取值范围为.
的取值范围为.
已知  ,且
,且  ,
,  ,则下列不等式中正确的是( )
,则下列不等式中正确的是( )
 ,且
,且  ,
,  ,则下列不等式中正确的是( )
,则下列不等式中正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
执行右边的程序框图,输出的结果是18,则①处应填入的条件是( )
A . K>2?
B . K>3?
C . K>4?
D . K>5?
函数  的部分图象大致为( )
的部分图象大致为( )
 的部分图象大致为( )
的部分图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设  是定义在R上的奇函数,当
是定义在R上的奇函数,当  时,
时,  ,则
,则  .
.
 是定义在R上的奇函数,当
是定义在R上的奇函数,当  时,
时,  ,则
,则  .
.
在 中,内角
中,内角 ,
,  ,
,  所对的边分别为
所对的边分别为 ,
,  ,
,  .已知
.已知 ,
,  , 且
, 且 ,
,  为
为 边
边 、
、 上的动点,则
上的动点,则 的值可能为( )
的值可能为( )
 中,内角
中,内角 ,
,  ,
,  所对的边分别为
所对的边分别为 ,
,  ,
,  .已知
.已知 ,
,  , 且
, 且 ,
,  为
为 边
边 、
、 上的动点,则
上的动点,则 的值可能为( )
的值可能为( )
A . -12
B . -8
C . 0
D . 64
若  ,则z的共轭复数为( )
,则z的共轭复数为( )
 ,则z的共轭复数为( )
,则z的共轭复数为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
P为椭圆 +
+ =1(a>b>0)上异于左右顶点A1 , A2的任意一点,则直线PA1与PA2的斜率之积为定值﹣
=1(a>b>0)上异于左右顶点A1 , A2的任意一点,则直线PA1与PA2的斜率之积为定值﹣ , 将这个结论类比到双曲线,得出的结论为:P为双曲线
, 将这个结论类比到双曲线,得出的结论为:P为双曲线 ﹣
﹣ =1(a>0,b>0)上异于左右顶点A1 , A2的任意一点,则( )
=1(a>0,b>0)上异于左右顶点A1 , A2的任意一点,则( )
 +
+ =1(a>b>0)上异于左右顶点A1 , A2的任意一点,则直线PA1与PA2的斜率之积为定值﹣
=1(a>b>0)上异于左右顶点A1 , A2的任意一点,则直线PA1与PA2的斜率之积为定值﹣ , 将这个结论类比到双曲线,得出的结论为:P为双曲线
, 将这个结论类比到双曲线,得出的结论为:P为双曲线 ﹣
﹣ =1(a>0,b>0)上异于左右顶点A1 , A2的任意一点,则( )
=1(a>0,b>0)上异于左右顶点A1 , A2的任意一点,则( )
A . 直线PA1与PA2的斜率之和为定值 B . 直线PA1与PA2的斜率之积为定值
B . 直线PA1与PA2的斜率之积为定值 C . 直线PA1与PA2的斜率之和为定值
C . 直线PA1与PA2的斜率之和为定值 D . 直线PA1与PA2的斜率之积为定值
D . 直线PA1与PA2的斜率之积为定值
 B . 直线PA1与PA2的斜率之积为定值
B . 直线PA1与PA2的斜率之积为定值 C . 直线PA1与PA2的斜率之和为定值
C . 直线PA1与PA2的斜率之和为定值 D . 直线PA1与PA2的斜率之积为定值
D . 直线PA1与PA2的斜率之积为定值
已知f(x)=|ax﹣1|,若实数a>0,不等式f(x)≤3的解集是{x|﹣1≤x≤2}.
(Ⅰ)求a的值;
(Ⅱ)若  <|k|存在实数解,求实数k的取值范围.
<|k|存在实数解,求实数k的取值范围.
给出如下四个命题:①若“  且
且  ”为假命题,则
”为假命题,则  均为假命题;②命题“若
均为假命题;②命题“若  ,则
,则  ”的否命题为“若
”的否命题为“若  ,则
,则  ”; ③“
”; ③“  ,则
,则  ”的否定是“
”的否定是“  ,则
,则  ”;④在
”;④在  中,“
中,“  ”是“
”是“  ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
 且
且  ”为假命题,则
”为假命题,则  均为假命题;②命题“若
均为假命题;②命题“若  ,则
,则  ”的否命题为“若
”的否命题为“若  ,则
,则  ”; ③“
”; ③“  ,则
,则  ”的否定是“
”的否定是“  ,则
,则  ”;④在
”;④在  中,“
中,“  ”是“
”是“  ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A . 1
B . 2
C . 3
D . 4
设  ,
,  ,
,  ,且
,且  ,则下列不等式成立的是( )
,则下列不等式成立的是( )
 ,
,  ,
,  ,且
,且  ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A . 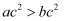 B .
B .  C .
C .  D .
D . 
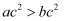 B .
B .  C .
C .  D .
D . 
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].

-
(1) 求图中a的值;
-
(2) 根据频率分布直方图,估计这100名学生语文成绩的平均分;
-
(3) 若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.

已知 ,
,  , 记
, 记 则A,B的大小关系是( )
则A,B的大小关系是( )
 ,
,  , 记
, 记 则A,B的大小关系是( )
则A,B的大小关系是( )
A . A>B
B .  C . A<B
D .
C . A<B
D . 
 C . A<B
D .
C . A<B
D . 
如图所示,△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长的线段是( )

A . AB
B . AD
C . BC
D . AC
如图是某班篮球队队员身高  单位:厘米
单位:厘米  的茎叶图,则该篮球队队员身高的众数是( )
的茎叶图,则该篮球队队员身高的众数是( )
 单位:厘米
单位:厘米  的茎叶图,则该篮球队队员身高的众数是( )
的茎叶图,则该篮球队队员身高的众数是( ) 
A . 168
B . 181
C . 186
D . 191
已知函数f(x)=cosx(x∈(0,2π))有两个不同的零点x1,x2,且方程f(x)=m有两个不同的实根x3,x4,若把这个数按从小到大排列构成等差数列,则实数m的值为 .
如图所示,向量![]() 在一条直线上,且
在一条直线上,且![]() 则( )
则( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 |
下列求导正确的是
A. (3x2-2)'=3x B. (log2x) '=![]()
C. (cosx) '=sinx D. (![]() )'=x
)'=x
已知函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域为( )
的定义域为( )
A.(-1,1) B.(-1,-![]() ) C. (
) C. (![]() ,1) D.(-1,0)
,1) D.(-1,0)
在 中,
中, ,
, ,
, 分别是内角
分别是内角 ,
, ,
, 的对边,若
的对边,若 ,
, ,
, ,则
,则 的面积等于( )
的面积等于( )
A. B.
B.  C.
C.  D. 3
D. 3
A.
最近更新
- 改革开放三十年来,中国的面貌发生了历史性变化。回答下列问题。在经济体制改革的同时,我国不断推进社会主义政治体制改革,积
- 如图1所示,质量为m的木块置于水平地面上,木块在与水平方向成θ角的拉力F作用下沿水平地面做匀速直线运动,木块与地面间的
- 《中国党内法规制定条例》和《中国党内法规和规范性文件备案规定》出台,自此中国首次拥有了正式的党内“立法法”。这体现了中国
- 干旱灾害是中国主要的气象灾害之一。下图反映了我国1950-1991年间不同区域季节分布及其对农业的影响,读图回答下列问题
- 如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=a(0<≦1
- If US software(软件) companies don’t pay more attention to qua
- 将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为.
- 人类祖先与猿分界的重要标志是( ) A.会使用天然工具
- 用下图装置测定种子萌发时进行的呼吸作用类型,同时关闭活塞,在25 ℃下经过20 min再观察红色液滴移动情况,下列对实验
- 碱基互补配对发生在下列哪些生理过程或生物技术中: ( ) ①种子的萌发 ②病毒的增殖过程
- 贾复字君文,南阳冠军人也。少好学,习《尚书》。事舞阴李生,李生奇之,谓门人曰:“贾君之容貌志气如此,而勤于学,将相之器也
- 空气吹出法是目前海水提溴的最主要方法之一。其工艺流程如图所示:(1)步骤④利用了SO2的还原性,反应的离子方程式为 __
- 《论语·颜渊》曰“颜渊问仁,子曰,克己复礼为仁,一曰克已复礼,天下归仁焉。”有人对这段话的解释是:“仁者,本心之全德。克
- 下列有关电化学的示意图中正确的是() A. B. C. D.
- 在一宗交通事故中,某人大脑受伤,不能说话但能听懂别人的说话,不能写字但能看书看报,那么受损的部位是()
- Becausehe was _______ the new limit,he was stopped and warn
- 以下说法正确的是( )A.纳米材料是指一种称为“纳米”的新物质制成的材料B.绿色食品是指不含任何化学物质的食品C.
- Authorities in Shanghai said Thursday night that anotherpers
- 等于A. B. C. D.
- 1mol某烃完全燃烧可得到2mol CO2,在一定条件下,1mol该烃能与2mol H2发生加成反应,这种烃是(



