高中 数学
《九章算术》是我国古代的数学巨著,内容极为丰富,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”,则其中分得钱数最多的是( )
A .  钱
B . 1钱
C .
钱
B . 1钱
C .  钱
D .
钱
D . 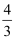 钱
钱
 钱
B . 1钱
C .
钱
B . 1钱
C .  钱
D .
钱
D . 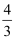 钱
钱
已知A,B两地相距100km.按交通法规规定:A,B两地之间的公路上车速要求不低于60km/h且不高于100km/h.假设汽车以xkm/h速度行驶时,每小时耗油量为( )升,汽油的价格是6元/升,司机每小时的工资是24元.
)升,汽油的价格是6元/升,司机每小时的工资是24元.
 )升,汽油的价格是6元/升,司机每小时的工资是24元.
)升,汽油的价格是6元/升,司机每小时的工资是24元.(1)若汽车从A地以64km/h的速度匀速行驶到B地,需耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从A地到B地的总费用最低?
已知集合A={x|ax2﹣3x﹣4=0,x∈R}.
-
(1) 若A中有两个元素,求实数a的取值范围;
-
(2) 若A中至多有一个元素,求实数a的取值范围.
若对任意的x1∈[e﹣1 , e],总存在唯一的x2∈[﹣1,1],使得lnx1﹣x1+1+a=x22ex2成立,则实数a的取值范围是( )
A . [  ,e+1]
B . (e+
,e+1]
B . (e+  ﹣2,e]
C . [e﹣2,
﹣2,e]
C . [e﹣2,  )
D . (
)
D . (  ,2e﹣2]
,2e﹣2]
 ,e+1]
B . (e+
,e+1]
B . (e+  ﹣2,e]
C . [e﹣2,
﹣2,e]
C . [e﹣2,  )
D . (
)
D . (  ,2e﹣2]
,2e﹣2]
已知  分别是
分别是  的内角
的内角  的的对边,若
的的对边,若  ,则
,则  的形状为( )
的形状为( )
 分别是
分别是  的内角
的内角  的的对边,若
的的对边,若  ,则
,则  的形状为( )
的形状为( )
A . 钝角三角形
B . 直角三角形
C . 锐角三角形
D . 等边三角形
设 ,
,  ,
,  , 则a,b,c的大小关系为( )
, 则a,b,c的大小关系为( )
 ,
,  ,
,  , 则a,b,c的大小关系为( )
, 则a,b,c的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知向量 , 且
, 且 , 则实数
, 则实数 的值为.
的值为.
 , 且
, 且 , 则实数
, 则实数 的值为.
的值为.
如图,在三棱柱 中,平面
中,平面 平面
平面 ,
,  ,
,  , 四边形
, 四边形 是菱形,
是菱形, ,
,  是
是 的中点.
的中点.
 中,平面
中,平面 平面
平面 ,
,  ,
,  , 四边形
, 四边形 是菱形,
是菱形, ,
,  是
是 的中点.
的中点.
-
(1) 证明:
 平面
平面 ;
;
-
(2) 求二面角
 的余弦值.
的余弦值.
函数f(x)=3sin(2x﹣  )的图象可以由y=3sin2x的图象( )
)的图象可以由y=3sin2x的图象( )
 )的图象可以由y=3sin2x的图象( )
)的图象可以由y=3sin2x的图象( )
A . 向右平移  个单位长度得到
B . 向左平移
个单位长度得到
B . 向左平移  个单位长度得到
C . 向右平移
个单位长度得到
C . 向右平移  个单位长度得到
D . 向左平移
个单位长度得到
D . 向左平移  个单位长度得到
个单位长度得到
 个单位长度得到
B . 向左平移
个单位长度得到
B . 向左平移  个单位长度得到
C . 向右平移
个单位长度得到
C . 向右平移  个单位长度得到
D . 向左平移
个单位长度得到
D . 向左平移  个单位长度得到
个单位长度得到
已知方程  表示的曲线是焦点在
表示的曲线是焦点在  轴上的椭圆,则
轴上的椭圆,则  的取值范围( )
的取值范围( )
 表示的曲线是焦点在
表示的曲线是焦点在  轴上的椭圆,则
轴上的椭圆,则  的取值范围( )
的取值范围( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知椭圆  ,过左焦点
,过左焦点  的动直线交椭圆于
的动直线交椭圆于  ,
,  两点,
两点,  为直线
为直线  上一定点(不是与
上一定点(不是与  轴的交点),直线
轴的交点),直线  ,
,  ,
,  的斜率分别为
的斜率分别为  ,
,  ,
,  .
.
 ,过左焦点
,过左焦点  的动直线交椭圆于
的动直线交椭圆于  ,
,  两点,
两点,  为直线
为直线  上一定点(不是与
上一定点(不是与  轴的交点),直线
轴的交点),直线  ,
,  ,
,  的斜率分别为
的斜率分别为  ,
,  ,
,  .
.
-
(1) 判断
 ,
,  ,
,  是否恒为等差数列,若是,给出证明;若不是,请说明理由;
是否恒为等差数列,若是,给出证明;若不是,请说明理由;
-
(2) 对任意给定的点
 ,是否都存在一条过点
,是否都存在一条过点  的直线
的直线  ,使得
,使得  ,
,  ,
,  为等比数列?请说明理由.
为等比数列?请说明理由.
已知 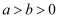 ,则
,则  的最小值为,取最小值时
的最小值为,取最小值时  的值为.
的值为.
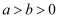 ,则
,则  的最小值为,取最小值时
的最小值为,取最小值时  的值为.
的值为.
已知 是椭圆E的两个焦点,P是E上的一点,若
是椭圆E的两个焦点,P是E上的一点,若 , 且
, 且 , 则E的离心率为( )
, 则E的离心率为( )
 是椭圆E的两个焦点,P是E上的一点,若
是椭圆E的两个焦点,P是E上的一点,若 , 且
, 且 , 则E的离心率为( )
, 则E的离心率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设随机变量![]() ,且
,且![]() ,则事件“
,则事件“![]() ”的概率为 (用数字作答)
”的概率为 (用数字作答)
求下列函数的导数:
![]() ;
;
已知在正项数列![]() 中,
中,![]() ,数列
,数列
![]() 项和.
项和.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅲ)若![]()
若直线![]() 与圆
与圆![]() 有公共点,则( )
有公共点,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
若数据x1,x2,x3,x4,x5的方差为3,则数据2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的方差为 .
若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
已知 是定义在上
是定义在上 的函数,那么“函数
的函数,那么“函数 在
在 上单调递增”是“函数
上单调递增”是“函数 在
在 上的最大值为
上的最大值为 ”的( )
”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
最近更新
- 若正六面体的一条对角线长为,则它的体积为( )A.1 B.2
- 某山共分布三类原生森林。下图显示三类森林每年每平方米净增的有机物质干重(NPP)与温度变化、降水量变化的关系。三类森林分
- 下列句子中加点成语的使用,不恰当的一项是 A.商业公司一般只让自己的业务员开拓市场,而不让其控制客户,以防备他们另起炉灶
- 第二节 书面表达(满分25分) 阅读下面一封来自于the Changchun Times的求助信,按照要求
- 反比例函数的图象在( )A.第一、三象限B.第一、四象限C.第一、二象限D.第三、四象限
- My motheroften ____________(担心)about my sister.
- 阅读下面材料,按要求答题。(共5分) 昨天,逐渐走出芦山地震阴霾的学生们迎来了复课的日子。各校第一课的主题不约而同选择了
- 人的血清白蛋白在临床上需求量很大,通常从人血中提取。由于艾滋病病毒(HIV) 等人类感染性病原体造成的威胁与日俱增,使人
- 如图,已知AD∥BC,要使四边形ABCD为平行四边形,需添加一个条件为______________.
- “一战”前后,下列哪一位创办的企业成为民族工商业的楷模( )A .张春 B .周学熙
- 土星的卫星很多,现已发现达数十颗,下表是有关土卫五和土卫六两颗卫星的一些参数,则两颗卫星相比较,下列判断正确的是 (
- 有7种物质:NH3、Mn2O3、ZnCl2、MnO2、NH4Cl、Zn和H2O,分别是锌—锰电池中氧化还原反应的反应物和
- 某工厂生产的某产品只含C、H、O三种元素,其分子模型如下图所示(图中球与球之间的连线代表化学键,如单键、双键等)。下列对
- (7分)已知硫酸锰(MnSO4)和过硫酸钾(K2S2O8)两种盐溶液在银离子催化下可发生氧化还原反应,生成高锰酸钾、硫酸
- 程序框图如右图所示,该程序运行后输出a的值是( ) (A)47 (B)94
- 1916年1月《农商公报》记载,“济南棉花之行情,日日变动。其原因,一方为需要供给之关系,他方为占输出棉花之大部分者,首
- 每年夏季,沿海海域都进入休渔期,期间,大小船只一律禁止捕鱼作业.你认为采取休渔期制度的根本目的是为了( )A.增
- 某地区工业发展不同阶段的生产与销售情况,读图完成下题。阶段Ⅱ与阶段Ⅰ相比,在阶段Ⅱ该地区企业发展的特点有 ①专业分工程度
- 如图所示,将两个相同的条形磁铁吸在一起,置于水平桌面上,下面说法正确的是A.B对桌面的压力的大小等于A、B的重力之和B.
- 下列生态系统中,自动调节能力较小的生态系统是A.海洋生态系统 B.森林生态系统C.湿地生态系统



