高中 数学
已知函数 定义域是,则
定义域是,则 的定义域是( )
的定义域是( )
 定义域是,则
定义域是,则 的定义域是( )
的定义域是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,l1l2是通过某市开发区中心O的南北和东西走向的两条道路,连接M,N两地的铁路是一段抛物线弧,它所在的抛物线关于直线l1对称,M到l1 , l2的距离分别是2km,4km;N到l1 , l2的距离分别是3km,9km.该市拟在点O的正北方向建设一座工厂,要求厂址到点O的距离大于5km,而不超过8km,并且铁路上任意一点到工厂的距离不能小于  km.则该厂离点O的最近距离为(工厂视为一点)( )
km.则该厂离点O的最近距离为(工厂视为一点)( )
 km.则该厂离点O的最近距离为(工厂视为一点)( )
km.则该厂离点O的最近距离为(工厂视为一点)( ) 
A . 6km
B . 6.5km
C . 6.25km
D . 7km
函数y=x2﹣4x+3,x∈[﹣1,1]的值域为( )
A . [﹣1,0]
B . [0,8]
C . [﹣1,8]
D . [3,8]
设  为任意正数.则
为任意正数.则  这三个数( )
这三个数( )
 为任意正数.则
为任意正数.则  这三个数( )
这三个数( )
A . 都大于2
B . 都小于2
C . 至少有一个不小于2
D . 至少有一个不大于2
若函数  的定义域是( )
的定义域是( )
 的定义域是( )
的定义域是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
已知正实数x,y,z满足x+y+z=2,则 的最大值是
的最大值是
 的最大值是
的最大值是
某几何体的三视图如图所示,则该几何体的体积为( )

A .  B .
B . 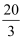 C .
C .  D .
D . 
 B .
B . 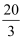 C .
C .  D .
D . 
如图,  的斜二测直观图为等腰
的斜二测直观图为等腰  ,其中
,其中  ,则
,则  的面积为( )
的面积为( )
 的斜二测直观图为等腰
的斜二测直观图为等腰  ,其中
,其中  ,则
,则  的面积为( )
的面积为( ) 
A . 2
B . 4
C .  D .
D . 
 D .
D . 
在平面直角坐标系中,  是圆
是圆  上的动点,满足条件
上的动点,满足条件  的动点
的动点  构成集合
构成集合  ,则集合
,则集合  中任意两点间的距离
中任意两点间的距离  的最大值为( )
的最大值为( )
 是圆
是圆  上的动点,满足条件
上的动点,满足条件  的动点
的动点  构成集合
构成集合  ,则集合
,则集合  中任意两点间的距离
中任意两点间的距离  的最大值为( )
的最大值为( )
A . 4
B .  C . 6
D . 12
C . 6
D . 12
 C . 6
D . 12
C . 6
D . 12
如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设P={质数},Q={偶数},则P∩Q等于( )
A . 1
B . 2
C . {2}
D . N
已知首项为1的等差数列  前
前  项和为
项和为  .
.
 前
前  项和为
项和为  .
.
-
(1) 若数列
 是以
是以  为首项、
为首项、  为公比的等比数列,求数列
为公比的等比数列,求数列  的前
的前  项和
项和  ;
;
-
(2) 若
 ,求
,求  的最小值.
的最小值.
函数  的值域为( )
的值域为( )
 的值域为( )
的值域为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:
![]()
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:
(1)b2 012是数列{an}中的第______项;
(2)b2k-1=________.(用k表示)
已知![]() ,
,![]() 是二次函数,
是二次函数,![]() 是奇函数,且当
是奇函数,且当![]() 时,
时,![]() 的最小值是1,求
的最小值是1,求![]() 的表达式.
的表达式.
若![]() ,则
,则![]() 的值是( )
的值是( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
.设{an}是等差数列,其前n项和为Sn(n∈N*);{bn}是等比数列,公比大于0,其前n项和为Tn(n∈N*).已知b1=1,b3=b2+2,b4=a3+a5,b5=a4+2a6.
(1)求Sn和Tn;
(2)若Sn+(T1+T2+…+Tn)=an+4bn,求正整数n的值.
若关于![]() 的方程
的方程![]() 有解,则实数
有解,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- 将一把钢尺紧按在桌面上,一端伸出桌边,拨动钢尺,听它振动发出的声音。改变钢尺伸出桌边的长度,再次用同样的力拨动,使钢尺两
- 20.名篇名句默写 (1)《念奴娇赤壁怀古》中,诗人凭吊英雄人物,抒发自己壮志难酬的苦闷心情,只好以一杯清酒祭月的语句是
- 请以高粱为原料,写出酿酒的化学反应方程式。
- 阅读下面短文,掌握其大意,然后从各题所给的四个选项中选出一个最佳答案。 After the war between Br
- 三段不可伸长的细绳 OA、OB、OC 能承受的最大拉力相同.它们共同悬挂一重物,如图所示,其中OB 是水平的,A、B 端
- 关于胚胎工程的正确叙述是 ()。 A.通过胚胎干细胞核移植可得到一群性状完
- 下列各句中加点的成语使用正确的一项是( ) A.他虽然犯了许多罪行,但罪不容诛,最后被判了无期徒刑。 B.他学
- 针对当下中学生常常流连网络却不愿静下心来阅读一些名著和经典的现象,请你写一段话劝告这些同学,让他们明白阅读的重要性和必要
- 选择填空 从 A、B、C 三个选项中选出一个能填入空白处的最佳选项。 Nancy and Kate are good
- 下列句子中没有语病的一项是(3分) A.近年来,中国学生留学出现明显低龄化,在这种需求的刺激下,一些以精细化培训为
- Itis necessary that parents should ________ the responsibil
- 在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物块速度v与时间t 的关系如图所示。取重力
- 2002年7月,52个非洲国家的领导人聚会南非德班国际会议中心,这标志着一个统管非洲政治、经济、军事、文化、社会等多方面
- 材料:为充分利用春节前后农闲季节的有利时机,磐石阳光办及早动手,积极开展阳光工程工作,已经唱响了农村劳动力培训转移的“三
- 下列各组物质均在试管里进行反应,反应过程中,在试管口观察不到红棕色气体出现的是( ) A.浓硝酸和铜片共热
- It’s reported that Ke Jie ______ by AlphaGoin May, 2017.
- 传说中带领人们治理黄河“三过家门而不入”的人是指A.炎帝 B.黄帝 C.尧
- 如图材料反映西周时期实行的A.禅让制B.分封制 C.郡县制D.行省制
- 2.依次填入下列横线处的成语,最恰当的一项是( ) ①马航失联事件中动用的军用卫星、军舰和飞机,都存在损耗问题,但所有这
- 如图所示,在同一轨道平面上,有绕地球做匀速圆周运动的卫星A、B、C某时刻在同一条直线上,则A.经过一段时间,A回到原位置



