高中 数学
函数f(x)=  x﹣sinx(x∈R)的部分图象是( )
x﹣sinx(x∈R)的部分图象是( )
 x﹣sinx(x∈R)的部分图象是( )
x﹣sinx(x∈R)的部分图象是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数 的部分图象如图所示,则函数f(x)的解析式为( )
的部分图象如图所示,则函数f(x)的解析式为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 已知曲线存在两条斜率为3的切线,且切点的横坐标都大于零,则实数
已知曲线存在两条斜率为3的切线,且切点的横坐标都大于零,则实数  的取值范围为.
的取值范围为.
若数列  共有k
共有k  项,且同时满足
项,且同时满足  ,
,  ,则称数列
,则称数列  为
为  数列.
数列.
 共有k
共有k  项,且同时满足
项,且同时满足  ,
,  ,则称数列
,则称数列  为
为  数列.
数列.
-
(1) 若等比数列
 为
为  数列,求
数列,求  的值;
的值;
-
(2) 已知
 为给定的正整数,且
为给定的正整数,且  ,
, ①若公差为

 的等差数列
的等差数列  是
是  数列,求公差d;
数列,求公差d;②若数列
 的通项公式为
的通项公式为 
 ,其中常数
,其中常数  ,判断数列
,判断数列  是否为
是否为  数列,并说明理由.
数列,并说明理由.
已知tanα=2,  =( )
=( )
 =( )
=( )
A .  B .
B .  C .
C . 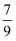 D .
D . 
 B .
B .  C .
C . 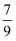 D .
D . 
已知函数  ,曲线
,曲线  在
在  处的切线为
处的切线为  .
.
 ,曲线
,曲线  在
在  处的切线为
处的切线为  .
.
-
(1) 解不等式
 ;
;
-
(2) 求证:直线
 与
与  在
在  内有且只有一个交点.
内有且只有一个交点.
已知非空集合A,B满足以下两个条件
 2,3,4,5,
2,3,4,5,  ,
,  ;
;
 若
若  ,则
,则  .
.
则有序集合对  的个数为
的个数为  )
)
A . 12
B . 13
C . 14
D . 15
已知  ,则
,则  的值为.
的值为.
 ,则
,则  的值为.
的值为.
设  是定义域为
是定义域为  的偶函数,若
的偶函数,若 
 ,都有
,都有  ,则
,则  ,
,  ,
,  的大小关系为( )
的大小关系为( )
 是定义域为
是定义域为  的偶函数,若
的偶函数,若 
 ,都有
,都有  ,则
,则  ,
,  ,
,  的大小关系为( )
的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设函数 , 则使得f(x)≥1的自变量x的取值范围是( )
, 则使得f(x)≥1的自变量x的取值范围是( )
 , 则使得f(x)≥1的自变量x的取值范围是( )
, 则使得f(x)≥1的自变量x的取值范围是( )
A . (﹣∞,﹣2]∪[1,2]
B . (﹣∞,﹣2)∪(0,2)
C . (﹣∞,﹣2]∪[0,2]
D . [﹣2,0]∪[2,+∞)
函数f(x)=  ﹣b(a>0)的图象因酷似汉字的“囧”字,而被称为“囧函数”.则方程
﹣b(a>0)的图象因酷似汉字的“囧”字,而被称为“囧函数”.则方程  =x2﹣1的实数根的个数为.
=x2﹣1的实数根的个数为.
 ﹣b(a>0)的图象因酷似汉字的“囧”字,而被称为“囧函数”.则方程
﹣b(a>0)的图象因酷似汉字的“囧”字,而被称为“囧函数”.则方程  =x2﹣1的实数根的个数为.
=x2﹣1的实数根的个数为.
△ABC中,D在AC上,且  ,P是BD上的点,
,P是BD上的点,  ,则m的值是( )
,则m的值是( )
 ,P是BD上的点,
,P是BD上的点,  ,则m的值是( )
,则m的值是( )
A .  B .
B .  C .
C .  D . 1
D . 1
 B .
B .  C .
C .  D . 1
D . 1
已知等比数列{an}的第2项、第5项分别为二项式(2x+1)5展开式的第5项、第2项的系数.
-
(1) 求数列{an}的通项公式;
-
(2) 记数列{an}的前n项和为Sn , 若存在实数λ,使
 恒成立,求实数λ的取值范围.
恒成立,求实数λ的取值范围.
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:

-
(1) 估计该校男生的人数;
-
(2) 估计该校学生身高在170~185cm的概率;
-
(3) 从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
已知四棱锥  的顶点均在球
的顶点均在球  的球面上,底面
的球面上,底面  是矩形,
是矩形,  ,
,  ,
,  ,二面角
,二面角  大小为120°,当
大小为120°,当  面积最大时,球
面积最大时,球  的表面积为.
的表面积为.
 的顶点均在球
的顶点均在球  的球面上,底面
的球面上,底面  是矩形,
是矩形,  ,
,  ,
,  ,二面角
,二面角  大小为120°,当
大小为120°,当  面积最大时,球
面积最大时,球  的表面积为.
的表面积为.
已知  ,则下列结论正确的是( )
,则下列结论正确的是( )
 ,则下列结论正确的是( )
,则下列结论正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在平面内点  、
、  、
、  满足
满足  .
.
 、
、  、
、  满足
满足  .
.
-
(1) 求点
 的轨迹方程;
的轨迹方程;
-
(2) 点
 ,
,  在椭圆
在椭圆  上,且
上,且  与
与  轴平行,过
轴平行,过  点作两条直线分别交椭圆
点作两条直线分别交椭圆  于
于  ,
,  两点.若直线
两点.若直线  平分
平分  ,求证:直线
,求证:直线  的斜率是定值,并求出这个定值.
的斜率是定值,并求出这个定值.
已知圆心在x轴的正半轴上,且半径为2的圆C被直线  截得的弦长为
截得的弦长为 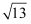 .
.
 截得的弦长为
截得的弦长为 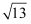 .
.
-
(1) 求圆C的方程;
-
(2) 设动直线
 与圆C交于
与圆C交于  两点,则在x轴正半轴上是否存在定点N,使得直线
两点,则在x轴正半轴上是否存在定点N,使得直线  与直线
与直线  关于x轴对称?若存在,请求出点N的坐标;若不存在,请说明理由.
关于x轴对称?若存在,请求出点N的坐标;若不存在,请说明理由.
已知  ,且
,且  ,则向量
,则向量  在
在  方向上的投影为( )
方向上的投影为( )
 ,且
,且  ,则向量
,则向量  在
在  方向上的投影为( )
方向上的投影为( )
A .  B .
B .  C . 1
D .
C . 1
D . 
 B .
B .  C . 1
D .
C . 1
D . 
已知椭圆 的离心率为
的离心率为 ,左顶点为A,右焦点为F,且|AF|=3.
,左顶点为A,右焦点为F,且|AF|=3.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点F做互相垂直的两条直线l1,l2分别交直线l:x=4于M,N两点,直线AM,AN分别交椭圆于P,Q两点,求证:P,F,Q三点共线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点F做互相垂直的两条直线l1,l2分别交直线l:x=4于M,N两点,直线AM,AN分别交椭圆于P,Q两点,求证:P,F,Q三点共线.
最近更新
- 在∠MON的两边上分别找两点P、Q,使得AP+PQ+QB最小。(保留作图痕迹,不要求作法)
- 关于交通运输中点的叙述,正确的是 ( ) A.
- 一物块以一定的初速度沿斜面向上滑,利用DIS实验系统,在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示。求:(1
- 如图所示为A、B两种固体物质的溶解度曲线,按要求完成下列小题:(1)A、B两种物质的溶解度都随温度的升高而,其中溶解度受
- 已知函数在时有最大值1,,并且时,的取值范围为. 试求m,n的值.
- 12.阅读下面的文字,完成(1)~(4)题。(25分) 千秋一寸心,红楼无限情 2012年5月31日凌晨,95岁高龄的红
- 小王在家电市场购买了一款1780元的小一匹空调,而小李花3800元购买了同一品牌的同匹数的空谰。两款空调价格不同的原因在
- 下列消化液中,不含消化酶的是() A. 胆汁 B.胰液 C. 肠液 D. 唾液
- On receiving my learner driver license a couple of months ag
- 某核反应方程为H+H→He+X.已知H的质量为2.0136 u,H的质量为3.0180 u,He的质量为4.0026 u
- 下表是日本进口的主要工业原料所占百分比及主要工业产品占世界市场百分比。下列关于日本工业的说法正确的是()A.工业原料全部
- 新疆分布的主要少数民族是( ) A.维吾尔族 B.壮族 C.哈萨克族 D
- 实验桌上有一包黑色粉末,为验证该粉末是否为铁粉,小明将磁铁放在黑色粉末上方,发现有黑色粉末被吸起来.就“将磁铁放在黑色粉
- 下列细胞结构属于生物膜系统的是 A.中心体 B.核糖体 C.染色体
- 图,在正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G. (1)观察图形,写出图中所有与
- 在显微镜下的洋葱表皮细胞是一个长方体,是下列哪个结构维持了这一形状的( )A、细胞壁 B、细胞
- 把一副扑克牌中的三张黑桃牌(它们的正面牌数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如
- 下列关于农村联产承包责任制的表述中,不正确的是 A.农产品全部由农民自行处理 B.改变了以往分
- 下列与反应式ADP + Pi + 能量ATP中“能量”相关的叙述正确的是 A.向右反应需要的能量可以来自细胞
- 下列关于酶的叙述,错误的是 A. 同一种酶可存在于分化程度不同的活细胞中 B. 低温能降低酶活性的原因是其破坏了酶的空间



