高中 数学
设函数  ,则该函数的最小正周期为,f(x)在
,则该函数的最小正周期为,f(x)在  的最小值为.
的最小值为.
 ,则该函数的最小正周期为,f(x)在
,则该函数的最小正周期为,f(x)在  的最小值为.
的最小值为.
连接双曲线  及
及  的4个顶点的四边形面积为
的4个顶点的四边形面积为 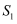 ,连接4个焦点的四边形的面积为
,连接4个焦点的四边形的面积为  ,则当
,则当 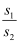 取得最大值时,双曲线
取得最大值时,双曲线  的离心率为( )
的离心率为( )
 及
及  的4个顶点的四边形面积为
的4个顶点的四边形面积为 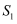 ,连接4个焦点的四边形的面积为
,连接4个焦点的四边形的面积为  ,则当
,则当 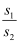 取得最大值时,双曲线
取得最大值时,双曲线  的离心率为( )
的离心率为( )
A . 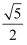 B .
B .  C .
C .  D .
D . 
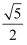 B .
B .  C .
C .  D .
D . 
设全集  ,已知集合则
,已知集合则  ,若
,若  ,则实数
,则实数  的取值范围是( )
的取值范围是( )
 ,已知集合则
,已知集合则  ,若
,若  ,则实数
,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知向量  与
与  互相垂直,其中
互相垂直,其中  .
.
 与
与  互相垂直,其中
互相垂直,其中  .
.
-
(1) 求sinθ和cosθ的值;
-
(2) 若
 ,
,  求cosφ的值.
求cosφ的值.
已知函数f(x)=2cos2  ﹣2
﹣2  sin
sin  cos
cos  ﹣1,x∈R.
﹣1,x∈R.
 ﹣2
﹣2  sin
sin  cos
cos  ﹣1,x∈R.
﹣1,x∈R. (I)求使得取f(x)得最大值的x的取值集合;
(II)若g(x)=x+f(x),求g(x)的单调递减区间.
将函数f(x)=sin(2x+  )的图象分别向左、右平移φ个单位,所得的图象关于y轴对称,则φ的最小值分别是( )
)的图象分别向左、右平移φ个单位,所得的图象关于y轴对称,则φ的最小值分别是( )
 )的图象分别向左、右平移φ个单位,所得的图象关于y轴对称,则φ的最小值分别是( )
)的图象分别向左、右平移φ个单位,所得的图象关于y轴对称,则φ的最小值分别是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知直线  经过抛物线
经过抛物线  的焦点,与
的焦点,与  交于
交于  两点,若
两点,若  ,则
,则  的值为.
的值为.
 经过抛物线
经过抛物线  的焦点,与
的焦点,与  交于
交于  两点,若
两点,若  ,则
,则  的值为.
的值为.
在极坐标系中,已知圆C的方程是ρ=4,直线l的方程是  .
.
 .
.
-
(1) 将直线l与圆C的极坐标方程化为直角坐标方程
-
(2) 求直线l与圆C相交所得的弦长.
设全集为U=R,集合A={x|x≤-3或x≥6},B={x|-2≤x≤14}.
-
(1) 求A∩B表示的集合.
-
(2) 已知C={x|2a≤x≤a+1},若C⊆B,求实数a的取值范围.
甲、乙两人进行投篮比赛,要求他们站在球场上的  ,
,  两点处投篮,已知甲在
两点处投篮,已知甲在  ,
,  两点的命中率均为
两点的命中率均为  ,乙在
,乙在  点的命中率为
点的命中率为  ,在
,在  点的命中率为
点的命中率为  ,且他们每次投篮互不影响.
,且他们每次投篮互不影响.
 ,
,  两点处投篮,已知甲在
两点处投篮,已知甲在  ,
,  两点的命中率均为
两点的命中率均为  ,乙在
,乙在  点的命中率为
点的命中率为  ,在
,在  点的命中率为
点的命中率为  ,且他们每次投篮互不影响.
,且他们每次投篮互不影响.
-
(1) 若甲投篮4次,求他至多命中3次的概率;
-
(2) 若甲和乙每人在
 ,
,  两点各投篮一次,且在
两点各投篮一次,且在  点命中计2分,在
点命中计2分,在  点命中计1分,未命中则计0分,设甲的得分为
点命中计1分,未命中则计0分,设甲的得分为  ,乙的得分为
,乙的得分为  ,写出
,写出  和
和  的分布列,若
的分布列,若  ,求
,求  的值.
的值.
已知向量 ,
,  , 则
, 则 ( )
( )
 ,
,  , 则
, 则 ( )
( )
A .  B . 2
C .
B . 2
C .  D .
D . 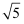
 B . 2
C .
B . 2
C .  D .
D . 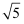
 是( )
是( )
A . 第一象限角
B . 第二象限角
C . 第三象限角
D . 第四象限角
命题p:“ ”,则“非p”为 ( )
”,则“非p”为 ( )
 ”,则“非p”为 ( )
”,则“非p”为 ( )
A .  B .
B .  ,
, C .
C .  D .
D . 
 B .
B .  ,
, C .
C .  D .
D . 
已知三棱柱ABC﹣A1B1C1的顶点都在球O的表面上,且侧棱垂直于底面ABC,若AC=4,∠ABC=30°,AA1=6,则球O的体积为.
如图,已知△ABC的两顶点坐标  ,
,  ,圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2,动点C的轨迹方程为.
,圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2,动点C的轨迹方程为.
 ,
,  ,圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2,动点C的轨迹方程为.
,圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2,动点C的轨迹方程为. 
若函数  (
(  ,且
,且  )的图像经过第二、三、四象限,则一定有( ).
)的图像经过第二、三、四象限,则一定有( ).
 (
(  ,且
,且  )的图像经过第二、三、四象限,则一定有( ).
)的图像经过第二、三、四象限,则一定有( ).
A .  ,且
,且  B .
B .  ,且
,且  C .
C .  ,且
,且  D .
D .  ,且
,且 
 ,且
,且  B .
B .  ,且
,且  C .
C .  ,且
,且  D .
D .  ,且
,且 
如图,△ABC中,∠C=90°,AC=16 cm,BC=8 cm,一动点P从点C出发沿着CB方向以2 cm/s的速度运动,另一动点Q从A出发沿着AC边以4 cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).

(1)若△PCQ的面积是△ABC面积的![]() ,求t的值.
,求t的值.
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
如图2,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则的AF长为 .

对于二次函数y=−4x2+8x−3,
(1)指出图象的开口方向、对称轴方程、顶点坐标;
(2)求函数的最大值或最小值;
设全集U=R,集合A={x|x≤1或x≥3},集合B={x|k<x<k+1,k∈R},且B∩∁UA≠∅,则( )
A.k<0或k>3 B. 2<k<3 C. 0<k<3 D. -1<k<3
最近更新
- 关于环绕地球运行的卫星,下列说法正确的是() A.沿椭圆轨道运行的一颗卫星,在轨道不同位置可能具有相同的速率 B.在赤道
- 某地发掘出一座古墓,发现墓室中有唐三彩马、景德年间的瓷罐、玉米残粒等。据此推断这座古墓的主人最早可能生活在 A.唐朝
- 下图是等高距相同的四幅地形图,有关a、b、c、d四处坡度大小的说法,正确的是( )A.a>c>d>
- He pretended to be French, but his German accent _______.A.
- 下列有关工业生产的叙述中错误的是 A.电解氯化钠溶液制金属钠 B.石灰石是炼铁和制玻璃的原料之一
- 下列各组词语中,没有错别字的一组是( ) A.专诚 焕然 一炷香
- 为反抗外来侵略,中国人民进行了不屈不饶的抗争,历史上有很多可歌可泣的英雄事迹和著名的战争。请将下面的不同时期的战争,按照
- 如上右图所示的程序计算,若输入x的值为1,则输出y的值为 。
- 在电影电视等文艺作品中,人们经常会看到臣民把皇帝称为“陛下”的情景。“陛下”本来是指宫殿的台阶,又特指皇帝座前的台阶。皇
- .已知,若A、B、C三点共线,则为 A. B. C. D.2
- – Has the Wuhan-Guangzhou high-speed railway been put into u
- 阅读下面的短文,然后按照要求,写一篇150词左右的英语短文。 China news,Shanghai,October8-
- 如图所示,甲、乙两池电极材料都是铁棒与碳棒, 请回答下列问题: (1)甲池为____________池 甲池中铁极的电极
- (10哈尔滨9).下列物质的应用不正确的是( ) 用水浇灌庄稼不锈钢用于制餐具氧气用于植物光合作
- 依次填入下列句子横线上的成语,恰当的一项是( ) ①这几幅画是他的早期作品,自是不能和他现在的创作
- 在图12-甲所示的电路中,合上开关S,电流表A1、A2的示数如图乙所示,则电流表A1的示数为 ,灯L1中的电流
- 下列物质分类正确的是()A. 单质:锌、铁、氢气、氮气 B. 易燃气体:氢气、氧气 C. 氧化物:水、氧化镁、氯酸钾 D
- 广州沙面至今仍保存着大量的西洋式建筑。这种现象反映的社会状况是( ) A.洋务运动全面开展
- 设集合A={x|0<x-m<3},B={x|x≤0或x≥3},分别求满足下列条件的实数m的取值范围: (1)
- 下列有关金属的冶炼说法不正确的是 A.电解熔融氯化钠制取金属钠的反应中,钠离子被还原,氯离子被氧化 B.湿法炼铜与火法炼



