高中数学：高一　 高二　 高三　 高考　

高中数学

已知椭圆E： $\text{[math]}$ ，不经过原点O的直线l：y=kx+m（k＞0）与椭圆E相交于不同的两点A、B，直线OA，AB，OB的斜率依次构成等比数列．

（Ⅰ）求a，b，k的关系式；

（Ⅱ）若离心率 $\text{[math]}$ 且 $\text{[math]}$ ，当m为何值时，椭圆的焦距取得最小值？

如图，正方体 $\text{[math]}$ 的棱长为1，线段 $\text{[math]}$ 上有两个动点E、F，且 $\text{[math]}$ ，则下列结论中正确的是（）

A . 线段 $\text{[math]}$ 上存在点E、F使得 $\text{[math]}$ B . $\text{[math]}$ 平面ABCD C . $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积相等 D . 三棱锥A-BEF的体积为定值

已知 $\text{[math]}$ ABC中， $\text{[math]}$ A $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ =．

已知复数z=（1﹣i）（i﹣2），则|z|=．

设 $\text{[math]}$

（1） $\text{[math]}$ 恒成立，求实数 $\text{[math]}$ 的取值范围；
（2）求证：当 $\text{[math]}$ 时， $\text{[math]}$ ．

已知集合A={a₁ ， a₂ ， a₃ ， …，a_n}，其中a_i∈R（1≤i≤n，n＞2），l（A）表示a_i+a_j（1≤i＜j≤n）的所有不同值的个数．

（1）已知集合P={2，4，6，8}，Q={2，4，8，16}分别求l（P），l（Q）；

（2）求l（A）的最小值．

已知函数f（x）由下表给出：

x	0	1	2	3	4
f（x）	a₀	a₁	a₂	a₃	a₃

其中a_k=（k=0，1，2，3，4）等于在a₀ ， a₁ ， a₂ ， a₃中k所出现的次数．

则a₄=； a₀+a₁+a₂+a₃=．

关于函数 $\text{[math]}$ ，描述正确的是（）

A . $\text{[math]}$ 的定义域为 $\text{[math]}$ B . $\text{[math]}$ 有 $\text{[math]}$ 个零点 C . $\text{[math]}$ 在定义域上是增函数 D . $\text{[math]}$ 是定义域上的奇函数

设实数x，y满足约束条件 $\text{[math]}$ 则z=x+2y的最小值为（）

A . 5 B . 3 C . 1 D . ﹣1

某理科考生参加自主招生面试，从7道题中（4道理科题3道文科题）不放回地依次任取3道作答．

（1）求该考生在第一次抽到理科题的条件下，第二次和第三次均抽到文科题的概率；
（2）规定理科考生需作答两道理科题和一道文科题，该考生答对理科题的概率均为 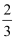$\text{[math]}$ ，答对文科题的概率均为 $\text{[math]}$ ，若每题答对得10分，否则得零分．现该生已抽到三道题（两理一文），求其所得总分X的分布列与数学期望E（X）．

已知函数 $\text{[math]}$ ．

（1）求 $\text{[math]}$ 的单调区间；
（2）求 $\text{[math]}$ 在区间 $\text{[math]}$ 上的最大值和最小值．

函数 $\text{[math]}$ ，关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有三个不同的实数解，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

一个空间几何体的三视图如图所示，则该几何体的表面积为（）

A . 48 B . $\text{[math]}$ C . $\text{[math]}$ D . 80

如果命题“曲线 $\text{[math]}$ 上的点的坐标都是方程 $\text{[math]}$ 的解”是正确的，则下列命题中正确的是（）

A . 曲线 $\text{[math]}$ 是方程 $\text{[math]}$ 的曲线 B . 方程 $\text{[math]}$ 的每一组解对应的点都在曲线 $\text{[math]}$ 上 C . 不满足方程 $\text{[math]}$ 的点 $\text{[math]}$ 不在曲线 $\text{[math]}$ 上 D . 方程 $\text{[math]}$ 是曲线 $\text{[math]}$ 的方程