高中 数学
将函数y=sin(ωx+φ)(ω>0,|φ|<π)的图象向右平移  个单位,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为y=sinx,则y=sin(ωx+φ)图象上距离y轴最近的对称轴方程为( )
个单位,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为y=sinx,则y=sin(ωx+φ)图象上距离y轴最近的对称轴方程为( )
 个单位,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为y=sinx,则y=sin(ωx+φ)图象上距离y轴最近的对称轴方程为( )
个单位,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为y=sinx,则y=sin(ωx+φ)图象上距离y轴最近的对称轴方程为( )
A . x=﹣  B . x=
B . x=  C . x=﹣
C . x=﹣  D . x=
D . x= 
 B . x=
B . x=  C . x=﹣
C . x=﹣  D . x=
D . x= 
已知cos(α+β)=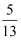 ,
, , α,β均为锐角,求sinα的值.
, α,β均为锐角,求sinα的值.
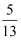 ,
, , α,β均为锐角,求sinα的值.
, α,β均为锐角,求sinα的值.
已知函数 , 点O为坐标原点,点
, 点O为坐标原点,点
 . 若记直线
. 若记直线 的倾斜角为
的倾斜角为 , 则tanQ1+tanQ2+……tanQn=( )
, 则tanQ1+tanQ2+……tanQn=( )
 , 点O为坐标原点,点
, 点O为坐标原点,点
 . 若记直线
. 若记直线 的倾斜角为
的倾斜角为 , 则tanQ1+tanQ2+……tanQn=( )
, 则tanQ1+tanQ2+……tanQn=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 ,则n=.
,则n=.
如图,在极坐标系Ox中,圆O的半径为2,半径均为1的两个半圆弧 ,
,  所在圆的圆心分别为
所在圆的圆心分别为 ,
,  , M是半圆弧
, M是半圆弧 上的一个动点.
上的一个动点.
 ,
,  所在圆的圆心分别为
所在圆的圆心分别为 ,
,  , M是半圆弧
, M是半圆弧 上的一个动点.
上的一个动点.
-
(1) 当
 时,求点M的极坐标;
时,求点M的极坐标;
-
(2) 以O为坐标原点,极轴Ox为x轴正半轴,
 的方向为y轴正方向建立平面直角坐标系.若点N为线段
的方向为y轴正方向建立平面直角坐标系.若点N为线段 的中点,求点N的轨迹方程.
的中点,求点N的轨迹方程.
已知函数 , 则
, 则 =( )
=( )
 , 则
, 则 =( )
=( )
A . 9
B .  C .
C .  D . 27
D . 27
 C .
C .  D . 27
D . 27
已知等比数列  的前n项和为
的前n项和为  ,且
,且  ,
,  ,则
,则  ( ).
( ).
 的前n项和为
的前n项和为  ,且
,且  ,
,  ,则
,则  ( ).
( ).
A .  B . 1
C .
B . 1
C .  D . 2
D . 2
 B . 1
C .
B . 1
C .  D . 2
D . 2
如图,吊车梁的鱼腹部分 是抛物线的一段,宽
是抛物线的一段,宽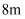 , 高
, 高 , 根据图中的坐标系,可得这条抛物线的准线方程为.
, 根据图中的坐标系,可得这条抛物线的准线方程为.
 是抛物线的一段,宽
是抛物线的一段,宽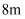 , 高
, 高 , 根据图中的坐标系,可得这条抛物线的准线方程为.
, 根据图中的坐标系,可得这条抛物线的准线方程为.
从集合A={﹣1,1,2}中随机选取一个数记为k,从集合B={﹣2,1,2}中随机选取一个数记为b,则直线y=kx+b不经过第三象限的概率为( )
A . 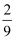 B .
B .  C .
C . 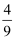 D .
D . 
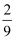 B .
B .  C .
C . 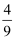 D .
D . 
过M(1,3)引圆x2+y2=2的切线,切点分别为A、B,则△AMB的面积为( )
A .  B . 4
C .
B . 4
C .  D .
D . 
 B . 4
C .
B . 4
C .  D .
D . 
已知集合  ,集合
,集合  .
.
 ,集合
,集合  .
.
-
(1) 若
 ,求实数
,求实数  的取值范围;
的取值范围;
-
(2) 是否存在实数
 ,使
,使  ?若存在,求出
?若存在,求出  的值;若不存在,说明理由.
的值;若不存在,说明理由.
不等式  的解集为.
的解集为.
 的解集为.
的解集为.
甲、乙两名学生的六次数学测验成绩(百分制)的茎叶图如图所示.

①甲同学成绩的中位数大于乙同学成绩的中位数;②甲同学的平均分比乙同学的平均分高;
③甲同学的平均分比乙同学的平均分低;④甲同学成绩的方差小于乙同学成绩的方差.
以上说法正确的是( )
A.③④ B.①② C.②④ D.①③④
如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 上,
上,![]() ,且
,且![]() 。
。
(I)判断直线![]() 的外接圆的位置关系并说明理由;
的外接圆的位置关系并说明理由;
(II)求![]() 的长。
的长。

在△ABC中,内角A,B,C所对的边分别为![]() ,且
,且![]() 则
则![]() =_______.
=_______.
求与椭圆![]() 有共同的焦点,且经过点M(2,
有共同的焦点,且经过点M(2,![]() )的椭圆的标准方程
)的椭圆的标准方程
是 。
已知等差数列![]() ,
,![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知![]() ,设函数
,设函数![]() 的图象在点
的图象在点![]() 处的切线为
处的切线为![]() ,则
,则![]() 在
在![]() 轴上的截距为 .
轴上的截距为 .
函数![]() ,若对任意
,若对任意![]() 恒成立,则实数
恒成立,则实数![]() 的取值
的取值
范围是______________.
已知函数![]() ,则
,则![]() =________;函数
=________;函数![]() 图象在点
图象在点![]() 处的切线方程为_______
处的切线方程为_______
最近更新
- 实数a在数轴上的位置如图所示,化简:=_______.
- 十二届全国人大一次会议上,政府工作报告不回避民生难题,直面民意关切,对会前民意调查中涉及的热点话题一一作了 “回应”。这
- ()构成了我国地形的骨架. A. 高原 B. 平原
- 离子液体是一种室温熔融盐,为非水体系.由有机阳离子、Al2Cl7﹣和AlCl4﹣组成的离子液体做电解液时,可在钢制品上电
- 阅读下面的文字,完成6―9题。 人类如何前往距地4.37光年的类地行星在距离地球个
- 与大棚种植蔬菜相关的措施及分析中,正确的是A.加大蔬菜的种植密度,可不断提高蔬菜的产量B.阴雨天适当提高大棚内温度,可明
- 下列中国古代科技成就对人类文明发展进程产生深刻影响的是 ( ) A.蔡伦改进的造纸术
- ---- Where’s Mr Zhang? ---- He ______ London. A. has beento
- 近年来,我国蔗糖产业逐步由福建、广东等地向广西、云南等地转移。“东蔗西移”、“东糖西移”一方面为东部产业发展提供了新的空
- 某主族元素最外层只有1个电子,则该元素一定是 A.金属元素 B.第ⅦA元素 C.第三周期元素
- 小明想在地图上找到叙利亚,最好选择哪种地图( )A.世界地形图 B.世界政区图 C.世界特大城市
- 下列四件光学仪器中,能对光有发散作用的是 ( ) A.平面镜 B.凸透镜 C.凹透
- 关于x的一元二次方程x(x-2)=2-x的根是( ) A.-1 B.0
- 阅读下面一首小诗,按要求完成作文。(60分)像大麦那样俯身蒂斯代尔(英) 像大麦那样俯身 在海滨的低田里, 在强劲的大风
- (12分)近代社会的民主思想与实践 材料 民主体制和随之而来的自由,随着社会的变化而演变。根据近代早期的英国法律,表达
- 2012年中央电视台每天推出的“数字十年”显示,“兴边富民”行动实施10多年来,逐步缩小了边境民族地区与发达地区的差距,
- 将S02通入Fe(NO3)3溶液中,溶液由棕黄色变为浅绿色,但立即又变为棕黄色;继续滴人BaC12 溶液,产生白色沉淀。
- 图是人体完成反射活动的神经结构示意图,请据图回答下列问题:(1)该图所示神经结构叫 。 (2
- 2.下列各句中,没有语病的一项是( ) A.10月26日,世界卫生组织发布报告,将培根、火腿、香肠等加工肉制品列为致
- 小文利用如图18甲所示的电路探究电流跟电阻的关系。已知电源电压为6V且保持不变,实验用到的电阻阻值分别为5Ω、10Ω、1



