高中数学：高一　 高二　 高三　 高考　

高中数学

若函数 $\text{[math]}$ (其中 $\text{[math]}$ 且 $\text{[math]}$ )，则 $\text{[math]}$ 的图像恒过定点．

设实数a，b满足a+2b=9．

（1）若|9﹣2b|+|a+1|＜3，求a的取值范围；
（2）若a，b＞0，且z=ab² ，求z的最大值．

定义在R上的函数y=f(x)，对任意不等的实数x₁,x₂都有[f(x₁)-f(x₂)](x₁-x₂)<0成立，又函数y=f(x-1)的图象关于点（1，0）对称，若不等式 $\text{[math]}$ 成立，则当1≤x<4时， $\text{[math]}$ 的取值范围是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

已知函数f（x）满足：f（m+n）=f（m）f（n），f（1）=3，则 $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +… $\text{[math]}$ 的值等于．（用含n的式子表示）

若将甲、乙、丙三个球随机放入编号为1，2两个盒子中，每个盒子的放球数量不限，则每个盒子中球数不小于其编号的概率是．

已知 $\text{[math]}$ ，则 $\text{[math]}$ 不可能满足的关系是（）

A .

B .

C .

D .

设各项均为正数的数列 $\text{[math]}$ 满足 $\text{[math]}$ $\text{[math]}$ ．

（Ⅰ）求 $\text{[math]}$ 的通项公式；

（Ⅱ）设 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的前n项和 $\text{[math]}$ ．

某多面体的三视图如图所示，其中正视图和侧视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.则该多面体的体积为（）

A . 8 B . 6 C . $\text{[math]}$ D . $\text{[math]}$

某校组织班班有歌声比赛，8个评委为某个班级打出的分数如茎叶图所示，则这些数据的中位数是（　　）

A . 84 B . 85 C . 86 D . 87.5

如图所示，在棱长为a的正方体ABCD－A₁B₁C₁D₁中，M ， N分别是AA₁ ， D₁C₁的中点，过D ， M ， N三点的平面与正方体的下底面相交于直线l.

（1）画出直线l的位置；
（2）设l∩A₁B₁＝P ，求线段PB₁的长．

为了得到函数 $\text{[math]}$ 的图象，只需将函数 $\text{[math]}$ 图象上（）

A . 所有点的横坐标伸长到原来的2倍，纵坐标不变 B . 所有点的横坐标缩短到原来的 $\text{[math]}$ 倍，纵坐标不变 C . 所有点沿y轴向下平移1个单位长度 D . 所有点沿x轴向右平移 $\text{[math]}$ 个单位长度

方程 $\text{[math]}$ 在区间 $\text{[math]}$ 上的解集为.

函数f（x）=（x³﹣3x）sinx的大致图象是（）

A .

B .

C .

D .

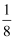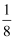设两条直线的方程分别为x+y+a=0，x+y+b=0，已知a，b是方程x²+x+c=0的两个实根，且0≤c≤ $\text{[math]}$ ，则这两条直线之间的距离的取值范围是．

已知tan（π﹣x）=2，

（1）求 $\text{[math]}$ 的值；
（2）求sin²x+sinxcosx﹣cos²x﹣2的值．

动点P在x轴与直线l：y＝3之间的区域（含边界）上运动，且点P到点F（0，1）和直线l的距离之和为4．

（Ⅰ）求点P的轨迹C的方程；

（Ⅱ）过点Q（0，－1）作曲线C的切线，求所作的切线与曲线C所围成的区域的面积．

如图，正方形ABCD的边长为3，E为DC的中点，AE与BD相交于F，则的值是

A． B． C． D．

已知球O是棱长为1的正方体的内切球，则平面截球O的截面面积为

A． B． C． D．

.已知x，y之间的一组数据：则y与x的回归方程必经过（　　）

A．（2，2） B．（1，3）

C．（1.5，4） D．(2，5)

若，则（　）

A. 　　　　 B. 　　　 C. 　　　 D.

最近更新

　