高中 数学
 的前
的前  项和为
项和为  ,且
,且  ,
,  .
.
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 若
 ,求
,求  的值.
的值.
 为奇函数.
为奇函数.
-
(1) 判断
 的单调性并证明;
的单调性并证明;
-
(2) 解不等式
 .
.
 ,
,  ,则
,则  与
与  夹角的余弦值为.
夹角的余弦值为.
 的图像经过点
的图像经过点 , 则
, 则 的值为( )
的值为( )

 B . 6
C . 4
B . 6
C . 4  D . 4
D . 4
 ,那么z的共轭复数在复平面上对应的点位于( )
,那么z的共轭复数在复平面上对应的点位于( )
 , 若函数
, 若函数 在
在 上为减函数,则实数a的取值范围为.
上为减函数,则实数a的取值范围为.
 .
.
-
(1) 求
 的值;
的值;
-
(2) 画出函数的图象.
 、
、  分别为双曲线
分别为双曲线  左、右支上的点,设
左、右支上的点,设 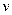 是平行于
是平行于  轴的单位向量,则
轴的单位向量,则  的最小值为.
的最小值为.
 若函数
若函数  恰有2个不同的零点,则实数
恰有2个不同的零点,则实数  的取值范围是.
的取值范围是.
 .
.
-
(1) 当
 时,求不等式
时,求不等式  的解集;
的解集;
-
(2) 若
 的定义域为
的定义域为  ,求
,求  的取值范围.
的取值范围.
 (t为参数,α≠0)经过椭圆C:
(t为参数,α≠0)经过椭圆C:  (φ为参数)的左焦点F.
(φ为参数)的左焦点F.
-
(1) 求实数m的值;
-
(2) 设直线l与椭圆C交于A、B两点,求|FA|×|FB|取最小值时,直线l的倾斜角α.
-
(1) 求直线AB的方程;
-
(2) 若直线l平行于直线AB,且到直线AB的距离为2,求直线l的方程.
设复数 


A . 2 B . 2 

椭圆![]() 内有一点
内有一点![]() ,
,![]() 为经过点
为经过点![]() 的直线与该圆截得的弦,则当弦
的直线与该圆截得的弦,则当弦![]() 被点
被点![]() 平分时,直线
平分时,直线![]() 的方程为。
的方程为。
一个项数为偶数的等差数列,其奇数项之和为24,偶数项之和为30,最后一项比第一项大21/2,则最后一项为 ( )
A、12 B、10 C、8 D、以上都不对
已知角![]() 的终边上有一点P(1,a),则
的终边上有一点P(1,a),则![]() 的值是 ( )
的值是 ( ) ![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
由曲线![]() 与
与![]() 的边界所围成区域的面积为( )
的边界所围成区域的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]()
![]() D. 1
D. 1
已知点F1,F2分别是双曲线![]() -
-![]() =1(a>0,b>0)的左、右焦点,过点F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是钝角三角形,则该双曲线的离心率的取值范围是( )
=1(a>0,b>0)的左、右焦点,过点F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是钝角三角形,则该双曲线的离心率的取值范围是( )
A.(1,+∞) B.(![]() +1,+∞) C.(1+
+1,+∞) C.(1+![]() ,+∞) D.(1,1+
,+∞) D.(1,1+![]() )
)
- 近年来,我国许多城市禁止汽车使用含铅汽油,主要原因是( ) A.提高汽油燃烧效率
- 鸟类的生殖和发育过程一般都经过求偶、交配、筑巢、产卵、孵卵、育雏等阶段,这些阶段都有例外,除了( ) A.求偶
- A~F分别是氢气、氧气、氮气、一氧化碳、二氧化碳、甲烷六种气体中的一种,请回答下列问题。(1)C与D在B中燃烧均能生成F
- 在制备细胞膜的实验中,把红细胞放入蒸馏水的目的是 A、溶解细胞膜 B、清洗细胞 C、使红细胞吸水涨破 D
- Seeing your picture, I couldn’t resist _____ the days _____
- I don’t have any money.He doesn’t have any money, .
- 如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管住下滑。已知这名消防队员的质量为60㎏,他从钢
- 四川自贡盛产食盐,下列关于食盐的说法中错误的是( )A.在食用盐中加入一定量的碘酸钾,可防止大脖子病B.食用盐不易
- 以下对洪仁玕与李鸿章在学习西方问题上的叙述正确的是 ( )A.两人都主张学习西方政治制度B.两人都不主张学习西方科学
- 马克思说:“罗马到处都由罗马法官根据罗马法进行判决,从而使地方上的社会秩序都被宣布无效……”对这段话的准确理解
- 读尼罗河和刚果河图,完成4~5题。4.图中两水系的支流密度差异很大,主要影响因素是A.气候 B.地形 C.纬度位置
- (08年宝鸡中学月考)(14分)航天飞机,可将物资运送到空间站,也可维修空间站出现的故障。(1)若已知地球半径为R,地球
- 下面有关发泡塑料饭盒的叙述,不正确的是 A.主要材质是高分子材料 B.价廉、质轻、保温性能好 C.适用于微
- ......
- 某名贵花卉用种子繁殖会发生性状分离。为了防止性状分离并快速繁殖,可以利用该植物的一部分器官或组织进行离体培养,发育成完整
- 小明在学习摩擦力一节时,为了探究滑动摩擦力跟正压力关系,设计了如图(甲)实验装置.实验器材有:木块、长木板、砂和砂桶、测
- 若O是△ABC所在平面内一点,D为BC边中点,且4++=0,那么( ) A. =B. = C. =2 D
- 一瓶溶液里可能含有OH—,Cl—,NO3—,CO32—,SO42—,五种阴离子中的某几种,现分别取溶液少许分装于两支试管
- 权力有两面性,为防止权力的滥用,需要对权力进行制约和监督。有效制约和监督权力的关键是 A.建立健全制约和监督机制
- 阅读下面的文字,完成下面各题。 谈阮籍之哭 谢宗玉 《晋书??阮籍传》是现存记录阮籍事迹最早的专著,其中记述了阮籍的两次



