高中 数学
下列函数中,最小正周期为π 且图象关于原点对称的函数是
①y=cos(2x+  ) ②y=sin(2x+
) ②y=sin(2x+  )③y=sin2x+cos2x ④y=sinx+cosx.
)③y=sin2x+cos2x ④y=sinx+cosx.
已知区间  ,
,  ,则
,则  .
.
 ,
,  ,则
,则  .
.
大熊猫活到十岁的概率是0.8,活到十五岁的概率是0.6,若现有一只大熊猫已经十岁了,则他活到十五岁的概率是( )
A . 0.8
B . 0.75
C . 0.6
D . 0.48
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1月份至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下数据:
|
日期 |
1月10日 |
2月10日 |
3月10日 |
4月10日 |
5月10日 |
6月10日 |
|
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这6组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
-
(1) 求选取的2组数据恰好是相邻两个月的概率;
-
(2) 若选取的是1月份与6月份的两组数据,请根据2月份至5月份的数据,求出
 关于
关于  的线性回归方程
的线性回归方程  ;
;
-
(3) 若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
参考公式:
 ,
,  .
.参考数据:
 ,
,  .
.
已知双曲线  的一个焦点与抛物线
的一个焦点与抛物线  的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于  ,则该双曲线的方程为( )
,则该双曲线的方程为( )
 的一个焦点与抛物线
的一个焦点与抛物线  的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于  ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示的一个算法的程序框图,则输出  的最大值为( )
的最大值为( )
 的最大值为( )
的最大值为( )
A .  B . 2
C .
B . 2
C . 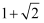 D .
D . 
 B . 2
C .
B . 2
C . 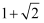 D .
D . 
设a,b,c是某三角形的三边长,证明a2(b+c﹣a)+b2(c+a﹣b)+c2(a+b﹣c)≤3abc.
若函数  的图像经过点
的图像经过点  ,则其图像必经过点( )
,则其图像必经过点( )
 的图像经过点
的图像经过点  ,则其图像必经过点( )
,则其图像必经过点( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知点P是矩形ABCD边上的一动点, 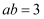 ,
, 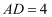 ,则
,则  的取值范围是.
的取值范围是.
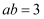 ,
, 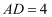 ,则
,则  的取值范围是.
的取值范围是.
下列五个写法:①  ;②
;②  ;③
;③  ;④
;④  ;⑤
;⑤  ,其中错误写法的个数为( )
,其中错误写法的个数为( )
 ;②
;②  ;③
;③  ;④
;④  ;⑤
;⑤  ,其中错误写法的个数为( )
,其中错误写法的个数为( )
A . 1
B . 2
C . 3
D . 4
已知函数f(x)=ax2﹣x﹣c,且不等式=ax2﹣x﹣c>0的解集为{x|﹣2<x<1},则函数y=f(﹣x)的图象为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  .
.
 .
.
-
(1) 当
 时,解不等式
时,解不等式  ;
;
-
(2) 若存在
 ,使得不等式
,使得不等式  的解集非空,求b的取值范围.
的解集非空,求b的取值范围.
已知函数f(x)对定义域R内的任意x都有f(x)=f(4﹣x),且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4则( )
A . f( )<f(3)<f(
)<f(3)<f( )
B . f(3)<f(
)
B . f(3)<f( )<f(
)<f( )
C . f(
)
C . f( )<f(3)<f(
)<f(3)<f( )
D . f(
)
D . f( )<f(
)<f( )<f(3)
)<f(3)
 )<f(3)<f(
)<f(3)<f( )
B . f(3)<f(
)
B . f(3)<f( )<f(
)<f( )
C . f(
)
C . f( )<f(3)<f(
)<f(3)<f( )
D . f(
)
D . f( )<f(
)<f( )<f(3)
)<f(3)
已知集合  {
{  },
}, 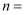 {
{  },若
},若  ,则实数a等于( )
,则实数a等于( )
 {
{  },
}, 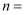 {
{  },若
},若  ,则实数a等于( )
,则实数a等于( )
A . 1
B . -1
C . ±1
D . ±1或0
已知二次函数 和
和
 和
和
(1)f(x)为偶函数,试判断g(x)的奇偶性;
(2)若方程g(x)=x有两个不相等的实根,当a>0时判断f(x)在(﹣1,1)上的单调性;
(3)当b=2a时,问是否存在x的值,使满足﹣1≤a≤1且a≠0的任意实数a,不等式f(x)<4恒成立?并说明理由.
已知函数f(x)=x﹣mex(m∈R,e为自然对数的底数)
-
(1) 讨论函数f(x)的单调性;
-
(2) 若f(x)≤e2x对∀x∈R恒成立,求实数m的取值范围;
-
(3) 设x1 , x2(x1≠x2)是函数f(x)的两个两点,求证x1+x2>2.
设实数  满足约束条件
满足约束条件  ,则
,则  的取值范围是.
的取值范围是.
 满足约束条件
满足约束条件  ,则
,则  的取值范围是.
的取值范围是.


己知函数![]() .
.
(1)求函数![]() 的增区间;
的增区间;
(2)是否存在实数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
如图,在正方体![]() 中,则
中,则![]() 与
与![]() 所成角的余弦值是
所成角的余弦值是![]()
![]()
A. ![]()
 B.
B. ![]()
C. ![]()
D. ![]()
最近更新
- 以下是用8mL蒸馏水稀释浓硫酸的实验操作过程,其中错误的环节是( )
- 为完善成品油价格机制,国家发展改革委员会决定对国内成品油价格机制设置调控上下限,当国际市场油价低于每桶40美元时,汽柴油
- 下列不能构成人体内环境的是() A. 淋巴 B. 细胞内液 C. 血浆 D.
- 下列运算正确的是() A.a2•a3=a6B.5a﹣2a=3a2C.(a3)4=a12D.(x+y)2=x2+y2
- 制备牛肉膏蛋白胨固体培养基的步骤是() A. 计算、称量、倒平板、溶化、灭菌 B. 计算、称
- “列强的炮声惊醒了古老中华帝国的美梦,中华民族的屈辱史——中国近代史开始了。”这里“列强的炮声”指的是( ) A.
- 笑气是人类最早应用于医疗的麻醉剂之一,笑气是氮的一种氧化物,该氧化物中氮元素的化合价为+1价,则笑气的化学式为() A.
- 下表是A、B、C、D、E五种有机物的有关信息: A B C D E ①能使溴的四氯化碳溶液褪色; ②比例模型为: ③能与
- 函数y=x|x(x-3)|+1( )A.极大值为f(2)=5,极小值为f(0)=1B.极大值为f(2)=5,极小值
- films in Feiyang Cinema this weekA WORLD WITHOUT TYHIEVES•
- 下列物质都需要密封保存,其中密封原因与空气中的成分无关的是A.浓硫酸 B.浓盐酸 C.生石
- 袋中装有m个红球和n个白球,m≥n≥2,这些红球和白球除了颜色不同以外,其余都相同.从袋中同时取出2个球,(1)若取出的
- 下组图片反映了现代国际关系中一系列重大事件。导致这些事件出现的共同原因是A.美苏冷战对峙 B.经济多极化
- (9分 每空1分)下图是动植物细胞亚显微结构模式图,请据图分析:w_w w. k#s5_u.c o*m 比较动植物细胞
- 历史上经历了共和国到帝国的演变,并大肆扩张领土成为地跨欧亚非三洲的国家的是( ) A.希腊 B.罗
- 力作用于物体产生的效果与力的_______、_________和_________有关,所以将它们称之为力的三要素。
- 空气是一种宝贵的资源,空气中可用作保护气和制造多种用途电光源的气体是( ) A. 氮气 B. 氧气 C.
- 读极地轮廓图,判断下列说法正确的是A.甲地有极昼极夜现象 B.乙地的经度为45。E C.丙地为中国
- More than one million children in the United States do not g
- 在探究“二力平衡条件”的实验中:(1)甲、乙两组同学分别选择器材后,设计组装的实验装置如图14所示。老师指出乙组同学选择




