高中 数学
要制作一个容积为9m3 , 高为1m 的无盖长方体容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总价是 元.
已知函数  .
.
 .
.
-
(1) 求f(x)的最小正周期;
-
(2) 求f(x)在区间
 上的最大值和最小值.
上的最大值和最小值.
从21 , 22 , 23 , …,2n这n个数中取m(n,m∈N* , 2≤m≤n)个数组成递增的等比数列,所有可能的递增等比数列的个数记为φ(n,m),则φ(100,10)=( )
A . 504
B . 505
C . 506
D . 507
在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马.已知四棱锥  为阳马,
为阳马,  底面
底面  ,其三视图如图所示,正视图是等腰直角三角形,其直角边长为2,俯视图是边长为2的正方形,则该阳马的表面积为( )
,其三视图如图所示,正视图是等腰直角三角形,其直角边长为2,俯视图是边长为2的正方形,则该阳马的表面积为( )
 为阳马,
为阳马,  底面
底面  ,其三视图如图所示,正视图是等腰直角三角形,其直角边长为2,俯视图是边长为2的正方形,则该阳马的表面积为( )
,其三视图如图所示,正视图是等腰直角三角形,其直角边长为2,俯视图是边长为2的正方形,则该阳马的表面积为( ) 
A .  B .
B .  C . 8
D .
C . 8
D . 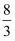
 B .
B .  C . 8
D .
C . 8
D . 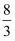
某校要求每位学生从8门课程中选修5门,其中甲、乙两门课程至多只能选修一门,则不同的选课方案有 种(以数字作答).
圆  经过点
经过点  且与圆
且与圆  内切,求圆心
内切,求圆心  的轨迹方程.
的轨迹方程.
 经过点
经过点  且与圆
且与圆  内切,求圆心
内切,求圆心  的轨迹方程.
的轨迹方程.
直线x+3y﹣7=0与圆x2+y2+2x﹣2y﹣3=0的交点A,B,则过A,B两点且过原点的圆的方程.
曲线y=1+  与直线y=k(x﹣2)+4有两个交点,则实数k的取值范围是( )
与直线y=k(x﹣2)+4有两个交点,则实数k的取值范围是( )
 与直线y=k(x﹣2)+4有两个交点,则实数k的取值范围是( )
与直线y=k(x﹣2)+4有两个交点,则实数k的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某工厂为了检验一条生产线生产的某种零件的质量,从该生产线生产的这种零件中随机抽取2000个,测量其长度(单位:厘米),将所得数据分成 ,
,  ,
,  ,
,  ,
,  五组,得到如图所示的频率分布直方图.已知零件长度在
五组,得到如图所示的频率分布直方图.已知零件长度在 内的是一等品,则该生产线生产的10000个零件中,估计一等品的数量是( )
内的是一等品,则该生产线生产的10000个零件中,估计一等品的数量是( )
 ,
,  ,
,  ,
,  ,
,  五组,得到如图所示的频率分布直方图.已知零件长度在
五组,得到如图所示的频率分布直方图.已知零件长度在 内的是一等品,则该生产线生产的10000个零件中,估计一等品的数量是( )
内的是一等品,则该生产线生产的10000个零件中,估计一等品的数量是( )
A . 3125个
B . 3750个
C . 4250个
D . 6250个
某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为cm.
已知函数  ,
,  ,则关于
,则关于  的方程
的方程  在区间
在区间  上的所有实根之和为( )
上的所有实根之和为( )
 ,
,  ,则关于
,则关于  的方程
的方程  在区间
在区间  上的所有实根之和为( )
上的所有实根之和为( )
A . -10
B . -8
C . -6
D . -4
在  中,
中,  为
为  边上一点,
边上一点,  ,
,  是
是  的中点,设
的中点,设  ,
,  ,则
,则  ( )
( )
 中,
中,  为
为  边上一点,
边上一点,  ,
,  是
是  的中点,设
的中点,设  ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数f(x)=lg(2cosx﹣1)的定义域为.
已知数列  的前
的前  项和为
项和为  ,且
,且  .
.
 的前
的前  项和为
项和为  ,且
,且  .
.
-
(1) 求
 的通项公式;
的通项公式;
-
(2) 若
 ,求数列
,求数列  的前
的前  项和
项和  .
.
如图,在直三棱柱ABCA1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=  ,M是CC1的中点.
,M是CC1的中点.
 ,M是CC1的中点.
,M是CC1的中点. 
-
(1) 求证:A1B⊥AM;
-
(2) 求二面角B-AM-C的平面角的大小..
已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
-
(1) 解不等式|g(x)|<5;
-
(2) 若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
已知圆心在![]() 轴上的圆
轴上的圆![]() 经过点
经过点![]() ,截直线
,截直线![]() 所得弦长为
所得弦长为![]() ,直线
,直线![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,当
两点,当![]() 为何值时,
为何值时,![]() 的面积最大.
的面积最大.
已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,过
,过![]() 且斜率为1的直线交
且斜率为1的直线交![]() 于
于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,其垂直平分线交
,其垂直平分线交![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .若四边形
.若四边形![]() 的面积等于7,则
的面积等于7,则![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
椭圆 ![]()
![]() 是参数
是参数![]() 的离心率是
的离心率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
一个几何体的三视图如图所示,则这个几何体的体积为( )
A.18 B.24 C.32 D. 36

最近更新
- 狼 一屠晚归,担中肉尽,止有剩骨。途中两狼,缀行甚远。 屠惧,投以骨。一狼得骨止,一狼仍从。复投之,后狼止而前狼又至。骨
- 引物与DNA母链的关系是() A.碱基顺序相同 B.长度相同 C.碱基互补配对
- 下列实验“操作和现象”与“结论”对应关系都正确的是( )选项 操作和现象 结论 A 将少量氯水加入KI淀粉溶液中,
- 适合生物呼吸的大气存在是地球上存在生命的重要条件之一,下列叙述与地球大气有密切关系的是( ) A.地球的质量与体积适中
- 艾弗里等人的肺炎双球菌转化实验和赫尔希与蔡斯的噬菌体侵染细菌实验都证明了DNA是遗传物质。这两个实验在设计思路上的共同关
- ―How did you like Nick’s performance last night?( ) ―To be
- Working in the kitchen for years made Tom ____ a good cook.
- 如图所示,质量为1kg可以看成质点的小球悬挂在长为0.9m的细线下端,将它拉至与竖直方向成θ =60°的位置后自由释放.
- “人的智力是按照人如何学会改变自然界而发展的”。这句话说明 A. 实践是认识的来源 B. 实践是认识的目的 C. 实践是
- 我国人口最多的省级行政区是 A.山东省 B.四川省
- 解放战争时期,中国的土地政策是( ) A、继续实行减租减息 B、实行土地公有制
- 下图曲线a表示使用诱变剂前青霉菌株数和产量之间的关系,曲线b、c、d表示使用诱变剂后青霉菌株数和产量之间的关系。下列说法
- 20.总书记指出:“要坚持权为民所用,情为民所系,利为民所谋。”这表明 A.中国的唯一宗旨是全心全意为人民服务 B.中国
- 依据下图所示,下列说法中,该图不能说明的是 A.原子是由原子核和核外电子构成的 B.原子是化学变化中的最小粒子 C
- A. can we learn B. we can learn C. did we learn
- 城市首位度,一般用一个地区最大城市与第二大城市人口规模之比来表示这个最大城市的首位度,通常用来反映该国或地区的城市规模和
- —Mary'salways _______ in reading and studying. —No wonder
- 如图,两根互相平行的长直导线过纸面上的M、N两点,且与直面垂直,导线中通有大小相等、方向相反的电流。a、o、b在M、N的
- 细胞是生物体和的基本单位.
- 番茄果皮红色(R)对黄色(r)为显性,若将纯种红色番茄(RR)的花粉授到黄色番茄(rr)的柱头上,则黄色番茄植株上所结种



