高中 数学
已知点P  在角
在角  的终边上,则
的终边上,则  .
.
 在角
在角  的终边上,则
的终边上,则  .
.
若函数 的零点为
的零点为 , 则
, 则 ( ).
( ).
 的零点为
的零点为 , 则
, 则 ( ).
( ).
A .  B . 1
C .
B . 1
C .  D . 2
D . 2
 B . 1
C .
B . 1
C .  D . 2
D . 2
直线  的一个法向量为.
的一个法向量为.
 的一个法向量为.
的一个法向量为.
已知命题  关于
关于  的函数
的函数  在
在  上是增函数,命题
上是增函数,命题  函数
函数  为减函数,若“
为减函数,若“  且
且  ”为假命题,则实数
”为假命题,则实数  的取值范围是( )
的取值范围是( )
 关于
关于  的函数
的函数  在
在  上是增函数,命题
上是增函数,命题  函数
函数  为减函数,若“
为减函数,若“  且
且  ”为假命题,则实数
”为假命题,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
若函数  同时满足以下三个性质;①
同时满足以下三个性质;①  的最小正周期为
的最小正周期为  ;②对任意的
;②对任意的  ,都有
,都有  ;③
;③  在
在  上是减函数, 则
上是减函数, 则  的解析式可能是( )
的解析式可能是( )
 同时满足以下三个性质;①
同时满足以下三个性质;①  的最小正周期为
的最小正周期为  ;②对任意的
;②对任意的  ,都有
,都有  ;③
;③  在
在  上是减函数, 则
上是减函数, 则  的解析式可能是( )
的解析式可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数f(x)= 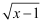 +
+  的定义域是 .
的定义域是 .
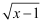 +
+  的定义域是 .
的定义域是 .
已知在△ABC中,|AB|=1,|AC|=2.
(Ⅰ)若∠BAC的平分线与边BC交于点D,求  ;
;
(Ⅱ)若点E为BC的中点,当  取最小值时,求△ABC的面积.
取最小值时,求△ABC的面积.
命题  ;命题
;命题  ,下列命题中为真命题的是( )
,下列命题中为真命题的是( )
 ;命题
;命题  ,下列命题中为真命题的是( )
,下列命题中为真命题的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若函数  是偶函数,则
是偶函数,则  的单调递增区间是( ).
的单调递增区间是( ).
 是偶函数,则
是偶函数,则  的单调递增区间是( ).
的单调递增区间是( ).
A .  B .
B .  C .
C .  D .
D . 
设等比数列{an}的公比q,前n项和为Sn . 若S3 , S2 , S4成等差数列,则实数q的值为.
Sigmoid函数是一个在生物学、计算机神经网络等领域常用的函数模型,其解析式为 , 则此函数在
, 则此函数在 上(填“单调递增”“单调递减”或“不单调”),值域为.
上(填“单调递增”“单调递减”或“不单调”),值域为.
 , 则此函数在
, 则此函数在 上(填“单调递增”“单调递减”或“不单调”),值域为.
上(填“单调递增”“单调递减”或“不单调”),值域为.
如图,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6。

-
(1) 求证:平面
 平面ACD;
平面ACD;
-
(2) 求二面角
 的平面角的正切值;
的平面角的正切值;
-
(3) 设过直线AD且与BC平行的平面为
 ,求点B到平面
,求点B到平面  的距离。
的距离。
若集合A={2,4,x},B={2,x2},且A∪B={2,4,x},则x=.
如图,多面体  中,四边形
中,四边形  为矩形,二面角
为矩形,二面角  为
为  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 中,四边形
中,四边形  为矩形,二面角
为矩形,二面角  为
为  ,
,  ,
,  ,
,  ,
,  ,
,  .
.

-
(1) 求证:
 平面
平面  ;
;
-
(2) 求直线
 与平面
与平面  所成角的正弦值.
所成角的正弦值.
 是定义在
是定义在  上的非负可导函数,且满足
上的非负可导函数,且满足  ,对任意正数
,对任意正数 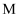 ,
, 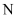 ,若
,若  ,则
,则  与
与  的大小关系是
的大小关系是 
 (请用
(请用  ,
,  或
或  )
)
计算:![]()
设定义域为![]() 的奇函数
的奇函数![]() 在区间
在区间![]() 上是减函数.
上是减函数.
(1)求证:函数![]() 在区间
在区间![]() 上是单调减函数;
上是单调减函数;
(2)试构造一个满足上述题意且在![]() 内不是单调递减的函数.(不必证明)
内不是单调递减的函数.(不必证明)
已知函数f(x)=e﹣2x﹣ax(a为常数)的图象与y轴交于点A,曲线y=f(x)在点A处的切线垂直于直线x+2y﹣1=0,则a的值为______.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)求函数
(2)若函数
已知椭圆  过点
过点 ,且一个焦点为
,且一个焦点为 .
.
(1)求椭圆 的方程;
的方程;
(2)若 为椭圆
为椭圆 的三条弦,
的三条弦, 所在的直线分别与
所在的直线分别与 轴交于点
轴交于点 ,且
,且 ,求直线
,求直线 的方程.
的方程.
(1)求椭圆
(2)若
最近更新
- 如图1所示,在a、b试管内的DNA都含有30对碱基。四个试管内都有产物生成,答:(1)a、d两试管内的产物是相同的,d试
- 下列事实不能说明分子之间有间隔的是() A.墙内开花墙外香 B.空气受热体积膨胀 C.氧气加压降温形成液氧 D.1体积酒
- 2011年3月11日,日本发生9级特大地震,造成人员和财产的巨大损失。据此回答问题. 20美国《科学美国人》发表文章指出
- 物体在同一平面内受F1、F2、F3三个共点力的作用处于平衡状态,当把F3的方向在同平面内旋转60°时(F3大小不变,F1
- 图6是“我国西气东输工程的管道分布图”,这项宏伟工程在2002年7月4日开工建设,于2004年8月3日全线贯通。它西起新
- 若右图中甲、乙两图均表示人体生命活动调节过程中细胞之间的信息传递方式,则以下相关叙述中不正确的是( )A.细胞2、细胞
- 读我国27°N局部地区剖面图,回答题。根据当地垂直植被带分布规律判断,甲处植被带应为 ( ) A.落叶阔叶林
- 把体积相同的甲烷和氯气充入一个集气瓶中,光照一段时间后,发现气体的黄绿色变浅,集气瓶壁上有淡黄色液滴,此时,集气瓶内的物
- 在“绿色化学”工艺中,理想的状态是反应物中的原子全部转化为期望的最终产物, 即原子的利用率为100%。下列反应类型中能体
- 人体细胞内能产生ATP的过程是()A. K+进入小肠上皮细胞 B. 葡萄糖氧化分解产生CO2和水 C. 胰岛细胞内将氨基
- 政府不能包办一切,但是政府该管的事情,必须真正管好,这是因为 ( ) A.政府是行政管理机关 B.政府是权力
- 下列关于劳动二重性的说法错误的是 ( ) A.具体劳动是使用价值的
- 现有一些物质的用途:用于生产①化肥,②肥皂,③火药,④玻璃,⑤印染,⑥洗涤剂.将以上物质的用途进行分类,并写出分类依据.
- Don’t play with the dog, Jack, for it _____________be danger
- (18分)如图所示,竖直平行导轨间距l=20cm,导轨顶端接有一电键K. 导体棒ab与导轨接触良好且无摩擦,ab的电阻R
- It’s not easy being a teenager—nor is it easy being the pare
- 如图7所示直线是真空中某电场的一条电场线,A、B是这条直线上的两点,一电子以速度vA经过A点向B点运动,经过一段时间后,
- 下列高原与它们各自的地形特点的连线组合,正确的是 ( )A.青藏高原-雪峰连绵
- 定义区间的区间长度为,已知函数的定义域为,值域为,求区间的长度的最大值与最小值的差
- 下列归类错误的是 选项 归 类 内 容 A 常见的碱



