高中 数学
综合题。
-
(1) (用分析法证明)

-
(2) 若a>0,b>0,c>0,且a+b+c=1求证:
 .
.
已知Rt△ABC,AB=3,BC=4,CA=5,P为△ABC外接圆上的一动点,且  的最大值是( )
的最大值是( )
 的最大值是( )
的最大值是( )
A .  B .
B .  C .
C .  D .
D . 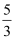
 B .
B .  C .
C .  D .
D . 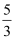
已知函数f(x)=cos(2x﹣  )+2sin(x﹣
)+2sin(x﹣  )sin(x+
)sin(x+  ).
).
 )+2sin(x﹣
)+2sin(x﹣  )sin(x+
)sin(x+  ).
).
-
(1) 求函数y=f(x)的单调增区间;
-
(2) 设△ABC的内角A,B,C的对边分别为a,b,c,满足c=2
 ,f(C)=1,且点O满足|
,f(C)=1,且点O满足|  |=|
|=|  |=|
|=|  |,求
|,求  •(
•(  +
+  )的取值范围.
)的取值范围.
已知函数  .
.
 .
.
-
(1) 判断
 的奇偶性并证明;
的奇偶性并证明;
-
(2) 若
 在
在  上的最大值为
上的最大值为  ,求a的值.
,求a的值.
已知某单位有甲、乙、丙三个部门,从员工中抽取7人,进行睡眠时间的调查.若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
-
(1) 用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
-
(2) 设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
下列图形所表示的几何体中,不是棱锥的为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若一条直线a与平面α内的一条直线b所成的角为30°,则下列说法正确的是( )
A . 直线a与平面α所成的角为30°
B . 直线a与平面α所成的角大于30°
C . 直线a与平面α所成的角小于30°
D . 直线a与平面α所成的角不超过30°
设F1 , F2为椭圆  =1的两个焦点,点P在椭圆上,若线段PF1的中点在y轴上,则
=1的两个焦点,点P在椭圆上,若线段PF1的中点在y轴上,则  的值为( )
的值为( )
 =1的两个焦点,点P在椭圆上,若线段PF1的中点在y轴上,则
=1的两个焦点,点P在椭圆上,若线段PF1的中点在y轴上,则  的值为( )
的值为( )
A . 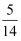 B .
B .  C .
C . 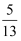 D .
D . 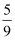
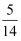 B .
B .  C .
C . 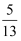 D .
D . 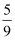
已知函数 , 则a,b,c的大小关系为( )
, 则a,b,c的大小关系为( )
 , 则a,b,c的大小关系为( )
, 则a,b,c的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 是数列
是数列  的前
的前  项和,若
项和,若  ,则
,则 
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,则cos∠DAC=( )
A .  B .
B .  C .
C .  D .
D . 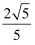
 B .
B .  C .
C .  D .
D . 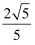
已知一组数据x1 , x2 , …,xn的方差s2=  ,其中
,其中  是这组数据的平均数.试证明s2=
是这组数据的平均数.试证明s2=  .
.
 ,其中
,其中  是这组数据的平均数.试证明s2=
是这组数据的平均数.试证明s2=  .
.
 中,
中, 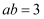 ,
,  ,
,  是
是  上的点,
上的点,  ,
,  。
。
-
(1) 求
 ;
;
-
(2) 求
 的面积。
的面积。
在①  ,②
,②  这两个条件中任选一个作为已知条件,补充到下面的横线上并作答.
这两个条件中任选一个作为已知条件,补充到下面的横线上并作答.
 ,②
,②  这两个条件中任选一个作为已知条件,补充到下面的横线上并作答.
这两个条件中任选一个作为已知条件,补充到下面的横线上并作答. 问题:  的内角
的内角  的对边分别为
的对边分别为  ,已知 .
,已知 .
-
(1) 求
 ;
;
-
(2) 若
 为
为  的中点,
的中点,  ,求
,求  的面积的最大值.
的面积的最大值.
在  中, 已知
中, 已知  ,则角
,则角  的大小为
的大小为
 中, 已知
中, 已知  ,则角
,则角  的大小为
的大小为
等比数列  的前
的前  项和为
项和为  ,若
,若  ,
,  ,则公比
,则公比  的值为( )
的值为( )
 的前
的前  项和为
项和为  ,若
,若  ,
,  ,则公比
,则公比  的值为( )
的值为( )
A .  B . 1
C .
B . 1
C .  或1
D .
或1
D .  或1
或1
 B . 1
C .
B . 1
C .  或1
D .
或1
D .  或1
或1
已知f(x)=  ,则f(x)+f(
,则f(x)+f(  )=.
)=.
 ,则f(x)+f(
,则f(x)+f(  )=.
)=.
用小于号连接  和
和  ,结果是.
,结果是.
 和
和  ,结果是.
,结果是.
已知函数![]() =
=![]() 的定义域是一切实数,则
的定义域是一切实数,则![]() 的取值范围是 ( ).
的取值范围是 ( ).
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
设![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
最近更新
- 2.(2012·广东理综)培育草莓脱毒苗所采用的主要技术是() A.组织培养 B.细胞杂交 C.显微注射
- 牛奶中含有乳球蛋白和酪蛋白等物质,在奶牛的乳腺细胞中,与上述物质的合成有密切关系的细胞结构是 A.线粒体、内质网、中心体
- 一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5m,消防车的云梯最大伸长为13m,则云梯可以达到该建
- 、分别是△的边、的中点,、分别是、的中点,若,则 .
- 某班以“新能源汽车的发展现状和未来”为主题,展开探究性学习。 老师给出了下列表格,让同学们以小组为单位进行研究。
- 如图6,为半圆的直径,平分,交半圆于点交于点,则的度数是____________.
- 已知等差数列的前项和为,若,,( 且). (1)求的值; (2)若数列满足,求数列的前项和.
- 阅读材料,回答问题。 材料一 2009年11月,中国商务部整合四个行业协会在美国有限电视新闻频道投放了关于“中国制造”
- 如图所示,用细线拴着的小球被拉到与悬点O等高的位置A由静止释放,小球从开始下摆到经过最低点B的过程中,错误的说法是(
- 下图中甲、乙、丙3个图分别表示某种雄性生物(假定只含两对染色体)的3个正在进行分裂的细胞,据图回答:(1)甲图表示
- 目前生态城市是现代城市建设的新潮流,它以环境为中心,注重可持续发展,强调资源的高效低耗和生态优先等原则,这有利于解决因不
- 下列说法正确的是 A.原子是不可再分的粒子 B.相对原子质量就是原子的实际质量 C.分子
- 淀粉溶液是一种胶体,并且淀粉遇到I2可以出现明显的蓝色特征。现将淀粉和Na2SO4溶液混合装在半透膜中,浸泡在盛蒸馏水的
- 某实验小组进行有关红磷燃烧的实验(如图). (1)红磷燃烧的表达式为. (2)如果进入水的体积超过瓶内空气体积的,其原因
- 四川省把扩大就业放在经济社会发展的突出位置,实施积极的就业政策,是在积极贯彻落实《中华人民共和国就业促进法》。实施积极的
- 在研究串联电路,引出“总电阻”概念时,所运用的科学研究方法是 ( ) A 控制变量法。 B
- 下列说法正确的是 ( )A. 卢瑟福的α粒子散射实验揭示了原子核有复杂结构B. 天然放射现象的发现揭示了原子核有
- 质量为0.5 kg的小球做竖直上抛运动,小球上升到最高点前1 s时的动量为p,从最高点下落1 s时的动量为p′,这2 s
- 有些动物有贮食行为,有的动物没有贮食行为,因此,贮食行为 A.是没有必要的
- 穿越时空隧道,我经商来到古希腊雅典,这里正在召开公民大会,人们纷纷涌向会场,当我想进入会场时却被拒之门外,你认为被拒之门



